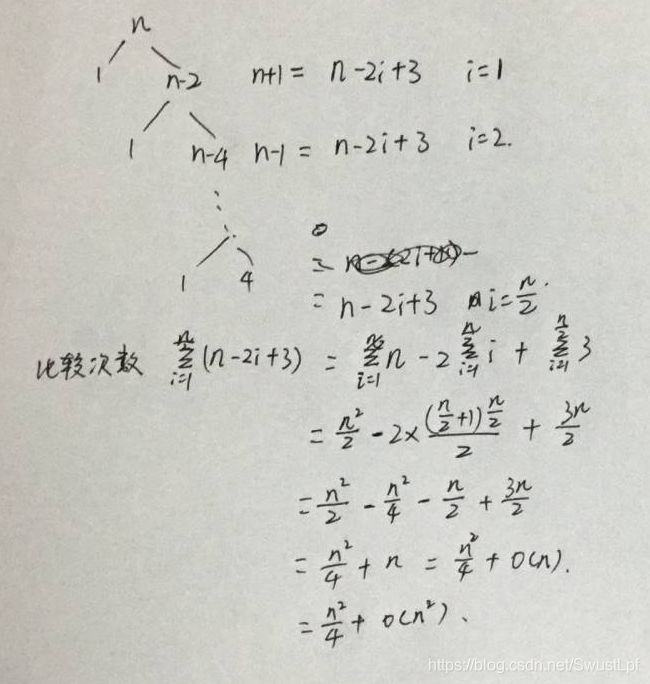2019上海科技大学991数据结构与算法

算法导论：
链接：https://pan.baidu.com
/s/1nXzwVML3V_FFnQHGFfBcYg 
提取码：50pq 

基础知识与结论

①：

$$满二叉树中，叶子节点=中间节点+1$$
满二叉树就是每个节点要么没有儿子，要么有两个儿子；当叶子节点增加两个儿子时，叶子节点增加两个，并且刚刚的叶子节点变成了中间节点，所以相当于中间节点和叶子节点都同时增加1，而最开始的情况的时候，就是只有1个根节点，相当于叶子节点为1，中间节点为0，而向以后发展两种节点增加的速度是一样的，所以总是相差1

②：

前序遍历：根左右
中序遍历：左根右
后序遍历：左右根

③：渐进号

$O$：最坏时间复杂度
$\Omega$：最好时间复杂度
$\Theta$：包含最好最坏复杂度（好像不太对）
$o$：感觉就是数学里的高阶无穷小的意思

真题

一.判断题（10 题，每题 2 分）

1.在循环链表中，某些链接域可能为空（错 ）
都是环了得哇，应该每个数的信息都一样，要是有一个空那全都空了

2.给定任意函数f(n)和g(n),f(n)=Q(g(n)和f(n)=o(g(n)可能同时成立。(错)
在算法导论的第三章21页

3. 一个好的哈希函数需满足简单均匀（对）

4.下列树是二叉搜索树。 （对）

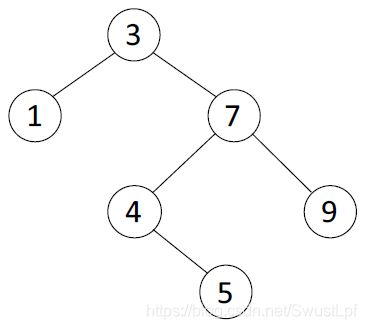
满足左儿子<根<右儿子
5.一棵树的节点个数有可能大于叶节点两倍。（对）
没说是二叉树哦(╥╯^╰╥)
随便一根长一点直链就能举出例子

6.图的邻接矩阵表示空间复杂度与边数无关。 （ 对）

7.在图的广度遍历算法中，每个节点恰好仅入队一次。 （ 对）

8.给定一个带权有向图，图的节点为1,2…n，要计算节点1和n之间的最短路径或判断这样的路径不存在，这个问题阔以在多项式时间内解决 （ 对）

9.给定一个 图，确中是否存在给定一个图正好包含100 个节点的团是一个 NP-complete的问 题， 假设 P≠NP （ ）

10.给定 一个图， 确定是否可以去除图中一半的节点后使得该可以三染色，这可以在多项式时间内完成， 假设 P≠NP （ ）

二.单选题（10 题，每题 2 分）

1.哪种字符串的存储结构可以方便地进行插入，删除，并联及重新安排子字符串?（ B）
A. 固定长度的存储结构
B. 链表存储结构
C. 具有固定最大长度的变存储结构
D. 数组存储结构
E. 以上都不是

2.下面哪个选项中的函数是按照渐进大小的增序排列？（C ）
A. 2n, n + (log n)2, n3, 10n2, n log n
B. n + (log n)2, n3, 10n2, n log n, 2n
C. n + (log n)2, n log n, 10n2, n3, 2n
D. n + (log n)2, 10n2, n log n, n3, 2n
E. 2n, n3, 10n2, n log n, n + (log n)2

3.存储 10 个元素到一个哈希表，这 10 个元素的 key 是{5,28,19,15,20,12,33,17,10,18}。哈希表总共有 9 个 slots，哈希函数是 h(k) = k mod 9，并用链表解决冲突。哈希表中最长的链表长度是？（ C）
mod之后：5 1 1 6 2 3 6 8 1 0
A. 1
B. 2
C. 3
D. 4

4.满二叉树的所有中间节点都有两个孩子节点。一个有 500 个叶子节点的满二叉树有多少个中间节点？（ B）
A. 250
B. 499
C. 500
D. 501
E. 1000

5.以下哪一个关于树的描述是错误的？（ A）
A. 非叶节点有可能没有孩子
B. 在一棵树中加一条边会形成一个环
C. 一棵树中并非每个节点都有父亲节点
D. 一棵包含一个节点的树高度为 0

A选项，不是叶子节点那下面不是肯定连着的吗？所以肯定有孩子呀
C选项是对滴，只剩一个根节点就没有父亲

6.下面二叉树的中序遍历是什么？（ A）

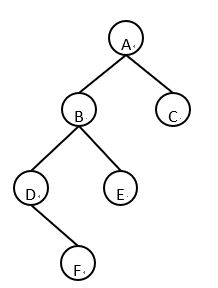
A. DFBEAC
B. ABDFEC
C. FDEBCA
D. FDEBAC

7.Prim 算法是一种计算图的最小生成树算法，Floyd-Warshall 算法可用于计算有向图中所有节点对之间的最短路径。以下哪些表述肯定是正确的？（B）

i. Prim 算法是一种贪心算法。
ii. Prim 算法是一种动态规划算法。
iii. Floyd-Warshall 算法是一种贪心算法。
iv. Floyd-Warshall 算法是一种动态规划算法。
A. i 和 iii
B. i 和 iv
C. ii 和 iii
D. ii 和 iv

8.以下哪一个图的问题可以在线性时间内解决？（ B）
A. 找到一个无向图中的最长简单环
B. 计算有向图的强连通分量
C. 解决带权有向图的单源最短路径问题
D. 找到一个无向图的最大团
汪同学说选B

9.下列关于归并排序和快速排序的陈述哪一项是对的？（ A）
A. 都是用分治法
B. 给定一个长度为 n 的输入数组，都是需要O(n)的时间进行每一次切分
C. 都有相同的最坏时间复杂度
D. 以上都对
我是感觉AB都对，但是汪同学说，归并并不划分，只是在并的时候才花时间，大概这个意思
10.任何一个基于比较的算法在一个长度为 n 的数组中同时找出最大和最小值，至少需要数组元素之间的比较的次数与下列哪个最接近？（B ）
A. n
B. 1.5n
C. 2n
D. n²

汪同学说见算法导论第九章第一页有证明，据说选B
哦~原来就是两个两个地拿进来比较，拿进来的这两个先比较一次，然后用小的比较最小值，大的比较最大值，这样每轮会比较3次，但是一共只会比较 $\frac{n}{2}$ 轮，总共就是 $\frac{3n}{2}$
试了一下，为啥优化后反而时间还长了喃(Ｔ▽Ｔ)，哦好像是产生的随机数太好了，如果换成递减数列，标答的方法就体现出来了~
改了一下，仅使用$if和=$
第三种方法是有位同学提出来的，我觉得很有道理。。。

#include"bits/stdc++.h"
#define Rand(L,R) (L+sui()%(R-L+1))
using namespace std;
const int maxn=1e8+5;
int a[maxn],N=maxn-5;
clock_t t1,t2;
int solve1()
{
     
	int Max=a[1],Min=a[1];
	t1=clock();
	for(int i=2;i<=N;i++)
	{
     
		if(a[i]>Max)Max=a[i];
		if(a[i]<Min)Min=a[i];
	}
	t2=clock();
	cout<<"Max="<<Max<<" Min="<<Min<<endl;
	return t2-t1;
}
int solve2()
{
     
	int Max=-1e9,Min=1e9;
	t1=clock();
	for(int i=1;i<=N;i+=2)
	{
     
		if(a[i]<a[i+1])
		{
     
			if(a[i]<Min)Min=a[i];
			if(a[i+1]>Max)Max=a[i+1];
		}
		else
		{
     
			if(a[i+1]<Min)Min=a[i+1];
			if(a[i]>Max)Max=a[i];
		}
	}
	t2=clock();
	cout<<"Max="<<Max<<" Min="<<Min<<endl;
	return t2-t1;
}
int solve3()//最好情况递减O(n),最坏情况递增O(2n) 
{
     
	int Max=a[1],Min=a[1];
	t1=clock();
	for(int i=2;i<=N;i++)
	{
     
		if(a[i]>Max)Max=a[i];
		else if(a[i]<Min)Min=a[i];
	}
	t2=clock();
	cout<<"Max="<<Max<<" Min="<<Min<<endl;
	return t2-t1;
}
int main()
{
     
	mt19937 sui(time(0));
	for(int i=1;i<=N;i++)a[i]=Rand(1,100000000);
	cout<<"优化前="<<solve1()<<endl;
	cout<<"优化后="<<solve2()<<endl;
	cout<<"第三种="<<solve3()<<endl;
 } 

三.多选题（5 题，每题 2 分）

1. 假设使用一个链表来表示一个稀疏矩阵，其中只存储非零元素。在链表的节点中需要存储什么信息？（ABCD ）
A. 行号
B. 列号
C. 矩阵元素的值
D. 非零元素的个数
E. 零元素的个数
有争议选不选D

2.在一个字符编码问题中，如果一个文件只由 a, b, c 组成，它们出现的频率分别是 45, 13,
12, 以下哪些编码是最优的？（D ）
A. a:000, b:010, c:101
B. a:000, b:010, c:100
C. a:00, b:01, c:10
D. a:1, b:01, c:00
大概是看他最短吧

3.给定一个具有 n 个节点和 m 条边的无向图，选择下列正确的称述？（ AC）
A. 如果该图是一棵树，那么m = n - 1
B. 如果该图是一棵树，那么n = m - 1
C. 如果该图是一个森林，那么m < n
D. 如果该图是一个森林，那么n < m
E. 以上都不正确

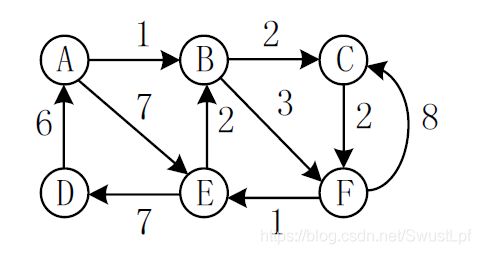
4.考虑以下带权无向图，以下哪一个或哪些表述是正确的？（ BCE）

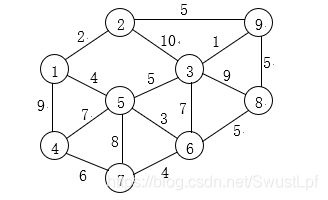
A. 上图有四个最小生成树
B. 存在一个包含边（6,8）的最小生成树
C. 存在一个包含边（5,6）的最小生成树
D. 所有最小生成树都包含边（2,9）
E. 所有最小生成树都包含边（4,7）


5.用 X ≤pY 表示问题 X 可以多项式时间规约到问题 Y。假设问题 X 属于 P，问题 Y 属于 NP，同时 X ≤p Y。下列哪些项一定为真？（A ）
A. X 属于 NP
B. X 是 NP-complete
C. Y 是 NP-complete
D. 假定 Z 属于 P，那么 Z ≤p X


据霍同学说是625页的这个(ಥ_ಥ)

四. Lists (25 points) 列表（25 分）

给定如下不含重复关键字的数组（数组的索引从 0 开始）：

（1）在如上数组中插入一个新的数据的平均时间复杂度是多少？用 O 表示这个时间复杂度，同时假设这个数组原来存放有 N 个数据、而且不满。（5 分）

我觉得是$O(\frac{N}{2})$

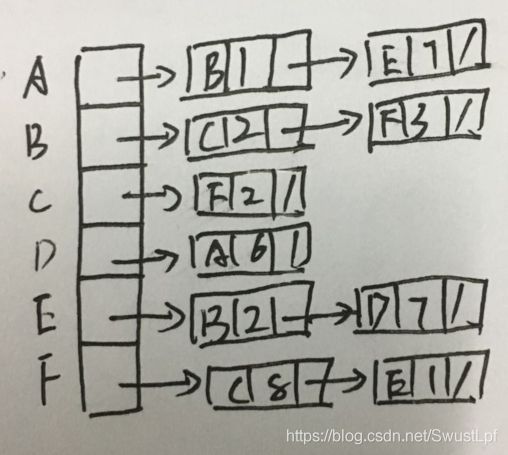
（2）用两个数组将上述给定的数组中的数据表示成一个单链表（需保持数据在原数组中的顺序），在两个数组中填写对应的信息（提示：其中一个数组存放关键字，另一个存放对应的指向下一个关键字的指针，用“／”表示 NULL 指针）。（5 分）
汪同学的答案，注意索引是从0开始滴：

（3）在以上两个数组表示的链表中去掉关键字 K3，画出去掉之后两个数组的状态（不被链表占用的空格留空）。（5 分）

同样是汪同学的答案：

（4）根据 (3)的结果，只给定了 K4 在关键字数组里的索引，要求把 K4 用$O(1)$时间复杂度从链表中删除，画出删除后的两个数组状态。（5 分）

这道题确实应该是这样的，因为题目说了要$O(1)$的复杂度，感谢群里的童鞋~

然后我才知道阔以$O(1)$删除邻接表的边，以前都没想过O(1)删除邻接表的边
（5）假设给定的关键字满足一个线性关系：K1 > K2 > K3 > K4 > K5。用一个完全二叉树将这个线性关系表示成一个二叉搜索树，然后将这个二叉搜索树用一个数组来表达，最后画出这个数组（数组的长度是 5）。备注：在这里完全二叉树是一个二叉树，其中每一层（可能除最后一层之外）都完全填充，而最后一层从左到右填到某一个位置为止。（5 分）
没懂这道题到底要干嘛，汪同学是先弄成二叉搜索树，然后一层一层填进数组里面

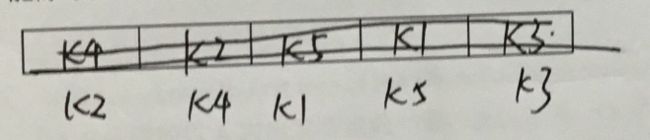
五.Binary Trees (25 points) 二叉树（25 分）

（1）请写出下面这棵二叉树的前序、中序、后序和广度优先遍历，以节点序列的形式给出。（9 分）


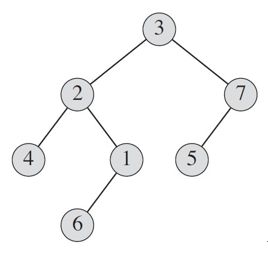
前序：3241675
中序：4261357
后序：4612573
广度优先：3274156
（2）一棵二叉树的前序遍历是 1,3,2,7,6,5,4，中序遍历是 1,2,3,4,5,6,7。请画出这棵树。（8 分）

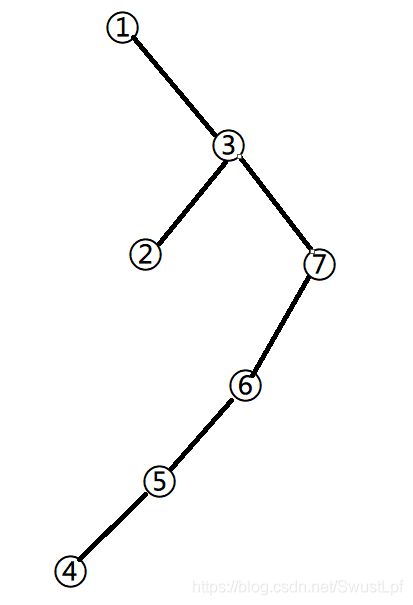
（3）一棵二叉树的后序遍历是 1,3,2,7,6,5,4，中序遍历是 1,2,3,4,5,6,7。请画出这棵树。（8 分）

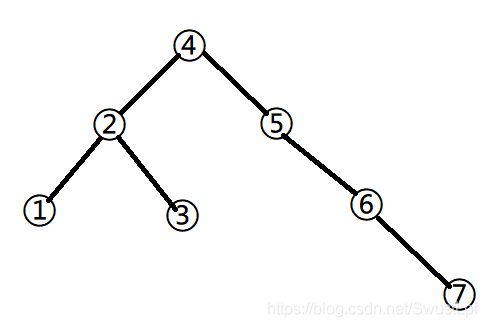
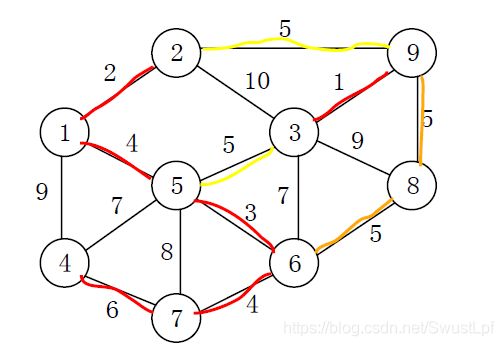
六. Graph (25 points) 图（25 分）

给定如下带权有向图

（1）画出该图的邻接表表示

（2）画出该图的邻接矩阵表示

（3）画出该图的以 A 为出发节点的一棵广度优先树

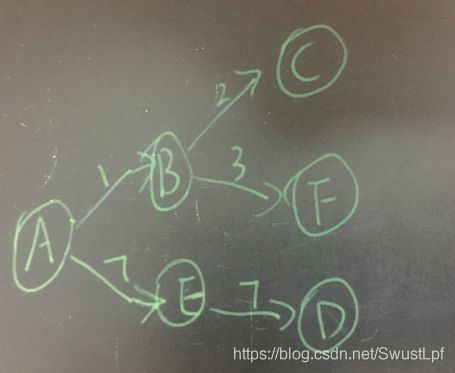
（4）画出该图的以 A 为出发节点的最短路径树。

七.快速排序（25 分）

假设我们把快速排序算法用在一个包含 n 个整数的数组 E，将这 n 个元素排为升序。我们用元素之间的比较次数来衡量时间复杂度，而每一次元素间的比较需要常数时间。
（1）假设一个快速排序算法的版本总是选数组里最左边的元素作为基准。对这样一个快速排序算法，找到一个最坏情况的包含 n 个元素的输入数组，用集合{1, 2, …, n}中的所有整数的一个排列来表示。对这样的输入，推导这个算法的渐近时间复杂度，用$O$来表示。（8 分）

解：
每次选的最左边的数都是最大的
$T(n)表示还有n个数需要排序$
$T(n)=T(n-1)+(n-1)$
$T(n)=T(n-2)+(n-2)+(n-1)$
$...$
$T(n)=T(1)+1+2+...(n-1)=\frac{n(n-1)}{2}=O(n^2)$
所以最坏情况就是$O(n^2)$

---

$O(nlogn)$的推导：
网上看到滴：
$T(n)=2T\left(\frac{n}{2}\right)+n$
$T(n)=2\left(2T\left(\frac{n}{4}\right)+\frac{n}{2}\right)+n=4T\left(\frac{n}{4}\right)+2n$
$T(n)=4\left(2T\left(\frac{n}{8}\right)+\frac{n}{4}\right)+2n=8T\left(\frac{n}{8}\right)+3n$
$...$
且$T(1)=0$
$T(n)=nT(1)+(\log (n))\times n=O(nlogn)$

（2）作为一个递归算法，快速排序算法一般要对很多小的子数组进行递归调用，从而影响了时间效率。 而插入排序算法在小数组上运行效率很高。描述一个修改快速排序算法的方法，利用插入排序算法来解决上述的问题。假设插入排序算法处理的每一个子数组的长度不超过 k 个元素。推导证明这个修改过的快速排序算法的平均时间复杂度是
O(nk + n lg(n / k))。（9 分）

解：
因为数组长度最少变成了$k$，所以快排只会递归$log(\frac{n}{k})$次，每次的排序都是$O(n)$的，因此整个快排的过程是$nlog\frac{n}{k}$的。然后长度为$k$的插入排序是$O(k^2)$的，有$\frac{n}{k}$坨，因此是$O(k^2\frac{n}{k})=O(nk)$
所以整个排序时间是$:O(nk+nlog\frac{n}{k})$

（3）假设快速排序算法总是从输入数组的第一个、最后一个、和中间位置这三个元素中选择中位数作为基准。证明该快速排序算法最坏情况下完成排序需作不超过$\frac{n^2}{4}+O(n^2)$次元素间的比较。（8 分）
汪同学的解答：