朋友,看过《决胜21点》没有?
讲麻省理工大学一华裔学生,拉了几个朋友去拉斯维加斯赌场,凭借对赌场的雕琢和研发的数牌体系,几年功夫赚了600万美元。(20世纪90年代哦!)
想象一下,你跟朋友一块儿喝酒,那小地方平时连100块都很少见,结果他一掏钱包,好家伙,一叠百元大钞。
俗话说知识就是力量,法国就是培根(hhh),学霸赚钱的方式就是清新脱俗,能不能带带咱!
还真能!
学霸大手一挥说,你们别来问哥了,哥出本书还不行?
然后他就出书了,就是下面这本——《大概率思维》,副标题也吸引人,叫“人生赢家都是概率赢家”。
《大概率思维》的作者叫马凯文,英文名Jeffrey Ma,是一位华裔天才。
我们都爱听“人生赢家”们讲话。看看马云跟他的朋友们,动不动身价几百亿,那就是金口玉言了呀,你听到耳朵里的那不是普通话,是人民币呀。
但很多时候,一件事成不成、一个人成不成,看人,也看天。
形势好了,鸭子下海都能穿越马六甲,形势不好,只能想着吉人自有天相。
但这位麻省学霸的书,就极吸引人了。
就算不能复制他驰骋赌场的光辉历史,咱朋友间打牌赢个百八十的,一礼拜的早餐钱不就有着落了?
要是出息点,把这套数牌体系用在投资理财、商业决策、人生规划上,也能赚上一大笔。毕竟当年,马凯文就是这么干的。
(而我基金定投都能亏,这就是传说中的马太效应吗!)
课代表划重点时间到了,看看在《大概率思维》中,马凯文都说了什么。
1. 像科学家一样理性思考
马凯文引用了《实习医生格蕾》中的一段话——
“伊兹,你是医生,是科学家,请像科学家一样思考。”
他提到,由于他们团队是靠概率赢得赌局的,会有很多人问他,要是同一张牌桌上有个“傻瓜”,不按套路出牌,那岂不是会扰乱正常的概率,让这种方法失效吗?
马凯文说,这就是所谓的“证实性偏差”——
“他只记得那个傻瓜及其决策伤害到他的个案,忘记了他从中受益的个案。”
证实性偏差在赌场外也会发生。
比如有假设说,911事件是布什政府内部所为,或者我们从未真正登上月球。
而那些证据确实“天衣无缝”,似乎都找不出破绽,但正因如此,才让我们看清其缺陷——为了证实一个假说,对其有利的数据和信息都被收集去了,但不利的呢,pia,直接剔除。
这让我想到高中的时候做物理实验,大家都是在追求“完美”的实验结果。咦?这个结果跟书本上的有点不一样,那绝对不能写到实验报告上去,要扣分哒!重新来过重新来过。
所以,你看到的答案都是别人想让你看到的,而不是真实的答案。
经济学上有“理性人”假说,就是假设每个人都是足够理性的。
这当然是不可能达到的啦。
只是我们在做决策,或者说理解事物的时候,可以更客观理性一些,便更有可能看到事件的全貌。
2. 数字真正的力量在于表示信息
马凯文说,数字真正的力量在于,它可以简洁地表示各种信息。量化能力是统计信息最有用的基本信息之一。
对此,我深表认同。
据说上海人民公园相亲角很有趣,那里如同求职中心一样,贴着各种各样的“启示”。不过,怎么写这启示,也是门学问。
你看着吧,光说“特别好看,身材好,学历高,收入尚可”的,肯定门前冷落鞍马稀。
但要是写了“颜值8分,170cm/55kg,美国伊利诺依大学毕业,年收入xxx万”,换我肯定停下来抄电话号码... ... 然后介绍给我那被催着找对象的表哥。
别觉得数字冷酷无情,相比模棱两可的形容词,准确的数字更加真实,更加落地。
马凯文将数字这种工具运用到了决策中。
他拿买车举例。
比方你决定买一辆车,如果只关心成本问题,那事情很简单,什么牌子、什么型号的车最便宜,百度一下就能知道。
但如果你说,除了价格,汽油里程数也很重要,环保和省油也是绝对不能忽略的... ... 那就复杂了。
对于选择困难症患者来说,需要权衡的变量一多,就容易想不清楚。
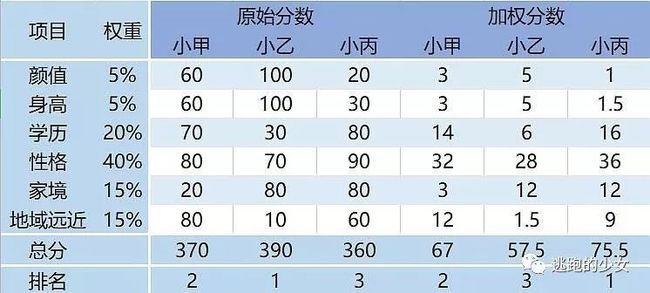
马凯文提出的解决方案是,一个问题如果有许多影响变量,且它们之间会有相互作用,那么你需要通过加权系统确认加入每个变量的方式。
这种方法,在其他方面也能得到应用,比如你家人为你安排了三个相亲对象,要思考与哪个多交流发展——
3. 不必苛求数据的完美,做实用的决策
前面我们讲的都是关于数学、概率、严谨和理性,但这一小节会有点不一样。
假设你现在开始赌博了,有个机器人在那边抛硬币,你可以押正面或者反面。
已知:已经连续11次都是正面了。问:下一场押正面赢的概率大,还是反面的概率大?再抛1000次,正面和反面出现的次数比会是多少?
我们在初中就学过概率问题,可以很快给出正确答案。
但是,人类真的是有人性的弱点的。
换作是我,就算再明白抛硬币正反面概率总是1/2,还是觉得押正面才稳得一匹。
我们的世界不同于21点世界这个完美的世界,不是所有事件都可能通过数学和统计学得到解释和预测。
马凯文提出“火热球手”这一概念,假设投手在投篮,如果一名投手上次投篮命中,那么他下次投篮的命中率会提高。
这在统计学上是显著性证伪的,但结合实际生活,好像的确会有这种情况。
不管是因为更自信了,发挥便更好,还是别的什么原因,有统计学算法没有衡量进去的算法,在悄然改变着事件背后的规律。
以前做概率的题,经常做到枪手射击命中率怎样怎样,还俩人比来比去。要我说,100次之后命中率通通往0算,因为枪手要被累死啦!
再复习下标题:不必苛求数据的完美,做实用的决策。
▲
Finally (finally to Finally!)
我们来总结一下《大概率思维》告诉我们的三个点——
1. 像科学家一样理性思考
2. 数字真正的力量在于表示信息
3. 不必苛求数据的完美,做实用的决策
在最后,说点私人的评价吧。
由于我对美国人玩的21点游戏比较陌生(兴趣也不高),而文中大篇幅谈论玩21点的方法论,让人有些接受无能,可能篇幅砍掉一点会更适合阅读。
另外,从书名“大概率思维”,和“人生赢家都是概率赢家”就能看出来,作者(或编辑)很努力想让这本书成为“大众的书”,但对我们而言,还是需要更多接地气的案例,来让书中的理论更为实用。
那么问题来了,你遇到过哪些有趣的概率问题?