2020年C题认证杯SEIR模型参数拟合
今年在参加认证杯的时候做到了传染病参数拟合,但是没有记录下来。这几天在做我们学校数学建模的校内赛的时候,也是有需要对SEIR模型进行函数的拟合。因此就发这个文章进行记录。
SEIR模型
- SEIR模型简介
- SEIR模型拟合
-
- 数据部分
- 求解过程
- 代码实现
- 总结
SEIR模型简介
首先就稍微介绍以下SEIR模型。
• S 为易感状态 (Susceptible),表示潜在的可感染人群,个体在感染之前是处于易感状态 的,即该个体有可能被邻居个体感染。
• E 为潜伏状态 (Exposed),表示已经被感染但没有表现出感染症状来的群体。
• I 为感染状态 (Infected),表示表现出感染症状的人,该个体还会以一定的概率感染其 能接触到的易感个体。
• R 为移除状态 (Removed),即个体或康复, 或因被隔离或死亡等原因而处于一种无传染性的净置状态.
画出状态转移图:

SEIR模型拟合
数据部分
首先就是为了验证模型的正确性,本篇文章不使用真实数据呈现结果,而采用Anylogic这个软件里面仿真数据,并且把它们存在data.xlsx下面。使用这个数据来进行参数拟合。在本次的模型中的参数有感染率 β=0.1,接触人数 r=10, 潜伏率 σ=0.2,康复率 γ=0.5 。总人口为5000。
仿真部分数据如下:
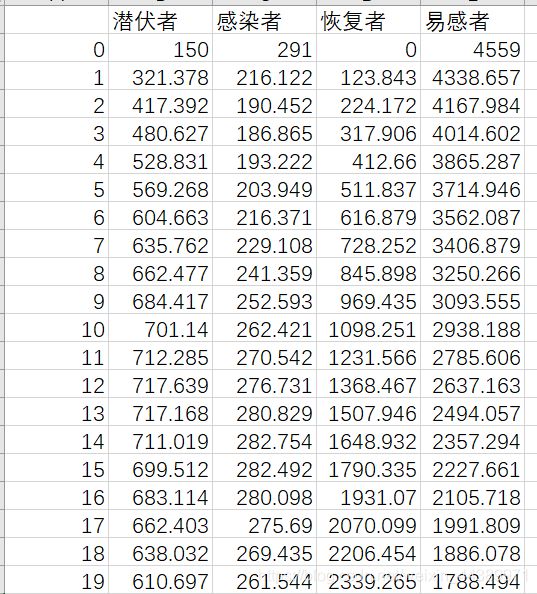
并且可以看到要流行就先要设置初始的潜伏者和感染者做为整个模型的动力。
求解过程
本题的求解思路,是根据上述的微分方程,通过最小二乘法找到误差的最小值即可。但是可能会陷入局部最优解而与实际值不同。
对于本问所选用的优化算法,我试了两个,一个是粒子群的函数,还有一个是fmincom函数,然后比较结果,我就展示后者。
后者的结果是:
可以看出来后面两个参数是准确的,前面的就比较大的偏差了,而且说函数的误差也还行。

但是在不知道实际参数的情况下,图像所呈现出来的结果是很不错的。而对于实际真实的SEIR模型而言,情形会变得复杂,包括数据的获取等等在这篇文章里面就不做演示。
代码实现
首先是第一个SEIR方程
function dp = seir_fun(t,p,beta,lamda,thta,gamma)
N = 5000;%总人口
dp = [5000-150-291,150,291,0]';%第一天的初始化人数
S = p(1);
E = p(2);
I = p(3);
R = p(4);
dp(1) = -beta*lamda*S * I / N;
dp(2) = beta*lamda* S * I / N - thta * E;
dp(3) = thta * E - gamma * I;
dp(4) = gamma * I;
end
接下来就是优化函数
function f = seir_Obj_fun(x)
global true_s true_e true_i true_r; % 在子函数中使用全局变量前也需要声明下
beta = x(1);
lamda = x(2);
thta = x(3);
gamma = x(4);
[~,p]=ode45(@(t,p) seir_fun(t,p,beta,lamda,thta,gamma), [1:1:76],[true_s(1) true_e(1) true_i(1) true_r(1)]);
f = sum(((true_s - p(:,1)).^2 + true_e - p(:,2)).^2 + (true_i - p(:,3)).^2 + (true_r - p(:,4)).^2);
end
主程序
clear;clc
d = xlsread('data.xlsx');
global true_s true_e true_i true_r
true_s = d(:,1);
true_e = d(:,2);
true_i = d(:,3);
true_r = d(:,4);
plot(1:76,true_s,'r-',1:76,true_e,'g-',1:76,true_i,'b-',1:76,true_r,'k-')
legend('S','E','I','R')
hold on
lb = [0.01 1 0.01 0.01]; ub = [1 20 1 1]; %设置拟合参数的取值范围以加快运行和取值合理
% fmincom函数
x0 = [0.01 1 0.01 0.01]
[x, fval] = fmincon(@seir_Obj_fun,x0,[],[],[],[],lb,ub)
T = 76;
beta = 0.3997;
lamda = 2.5018;
thta = 0.2;
gamma = 0.5;
[~,p]=ode45(@(t,p) seir_fun(t,p,beta,lamda,thta,gamma), [1:1:T],[true_s(1) true_e(1) true_i(1) true_r(1)]); %用拟合的参数进行参数估计
plot(1:T,p(:,1),'r*',1:T,p(:,2),'g*',1:T,p(:,3),'b*',1:T,p(:,4),'k*')%画出图像
总结
对于SEIR模型而言,今年就是一个很热门的模型。对于这个模型而言还是较为复杂,显然就算是完全拟合了数据,得到的参数也不是很符合实际。
上面的代码也是我琢磨了比较久的时间才得以运行,一开始是从清风老师对于SIR的直播课的代码的延伸再加上自己对于这个模型的琢磨,就得到了比较令人满意的拟合图像。但是由于自己现在的精力有限,无法对实际的中国参数进行拟合,大家在考虑实际问题的时候,可以去尝试深入地了解模型,简化和丰富模型。
对于优化函数的了解也是在听了恩达老师的机器学习课程才了解到具体使用。所以就还是想告诉大家,当你在学习的时候,眼前遇到困难没有办法解决的时候,你不用太纠结,可以先放一放,然后keep studying,当你回过头来再看问题的时候可能就会解决。
有什么问题和疑问可以交流和讨论,希望这篇文章能够确实地帮到你!那就感谢你看我的罗里吧嗦啦!

