先定个小目标:把1~9的全排列映射到0~9!-1上,并与其形成一一对应关系。
我从一个故事引入吧:
老王走到一个荒郊野岭,看到前面有九扇门,从左到右对应门牌号1~9,门前的空地上还有个液晶显示屏,上面有九个数字显示位。他把这个液晶显示屏捡了起来,然后随便选了一扇门(比方说7)进去,然后他看到液晶显示屏上第一位就变成了7。进去之后,又有门牌号从小到大排列的八扇门(1,2,3,4,5,6,8,9),他又选了第七扇门(也就是门牌号为8的门),然后液晶显示屏上面第二位又变成了7,再然后,里面又有七扇门(1,2,3,4,5,6,9),他选了第三个门进去(门牌号为3),然后液晶显示屏上第三位出现了数字3。最后老王的液晶显示屏上面显示了773122111(换句话说,他选的门牌号序列为783145269),同时,他在最里面的房间里面找到了一个箱子,打开一看,有张纸条,上面写着273630。
那么问题来了,液晶显示屏上面的数字是什么意思?根据老王开门的方式就知道,其实这个数字就表示了老王打开门的方式(先打开第七扇门,然后再打开剩下的门里面的第七扇门,然后是第三扇,以此类推),并且已经打开过的门的门牌号不会在后面再出现,最后老王一共开了九扇门,对应的门牌号序列是783145269,实际上这个过程就是对1~9的整数进行全排列的一个过程,773122111是选择次序,783145269是实际排列,很容易想象,只要次序确定,那么排列就一定是唯一确定的,并且次序数列中第一位有1~9九种可能,第二位有1~8八种可能,第三位为1~7七种,换句话说,从左到右数的第n位An的取值范围是{
An | 1≤An≤n, An∈Z}, 而且这个取值范围是不受前面选数方式干扰的。
到这里,我们就把1~9的9!个不同种排列方式与这9!个次序数列一一对应了,最小的次序数列为111111111,最大的为987654321。这种次序数列有很多优势,我这里说两点:
1)次序数列中每一位数的取值范围是相对连续的(如1~3,1~4,1~n)
2) 次序数列中每一位数的取值范围是相对独立的,不会因为其他位上数字的选取方式而发生改变
再来看看我们的小目标:把1~9的全排列映射到0~9!-1上,并与其行成一一对应关系。
现在我们已经可以把1~9的全排列与这9!个次序数列一一对应了,那么接下来的工作就是找到次序数列和0~9!-1的整数的一一对应关系。
在这之前,我们需要对次序数列做一些处理:因为最小的次序数列是111111111,而0~9!-1的整数中最小的是0,形式上
有些出入,我们就把这个次序数列的每一位都减去1,得到新的一个数列,其取值范围为000000000~876543210,其中从左到右数第i位Ai取值范围为{Ai
| 0≤Ai≤n-1,
Ai∈Z}。如果还用刚才老王的例子去理解,我们可以说,这个数字对应的是每次选择的门的时候此门左边门的个数(也即门牌号比该门小的门的扇数,如第一次选择了第七扇门,那么它左侧有6扇门,或者说比第七扇门门牌号小的门的个数为6)。
可以想象,000000000~876543210可以从小到大分别对应0~9!-1,这样
000000000对应的就是0,876543210对应的就是0~9!-1。那中间的数怎么办?别急,我们先来看看数组的工作方式(这里说的数组和C语言中的数组有些相似,但是不完全一样):
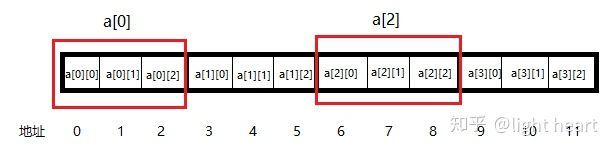
这是一个二维数组,其中最小单元所占长度为1,这样a[0]占3个长度,而a[0][0]就只占1个长度。我们为每个最小单元都编一个地址 (从0~11),这样你看到a[1][1]就知道它的地址为4,看到地址6就知道它对应的单元为a[2][0]。那么我们再问一下自己,我们到底是如何算出某一单元的地址的呢?其实,我们是先通过第一个参数1得到这个基本单元是在a[1]内的,也就是说其地址至少为3,然后我们看到第二个参数1,就知道它的地址其实是4了。这个地址可以理解为0+1*3+1+1, 其中,加粗的0表示第一个基本单元的地址,加粗的3表示一个一级单元所占的长度,加粗的1表示一个二级单元(这里是基本单元) 所占的长度。这种算法其实就是一个逐渐细化的过程,就好比是在一棵树上寻找某片叶子时,先确定它在哪个大的分支上,然后再在这个分支上继续确定更小的分支,这样最终就能找到这片叶子。
我相信你已经发现了数组的下标00~32与我们之前说的000000000~876543210是有些相似之处的,我们不妨就创立一个九维的数组,从左到右第一个是a[0][0][0][0][0][0][0][0][0](其地址为0),最后一个是a[8][7][6][5][4][3][2][1][0](其地址为9!-1),一共有九级单元,其中第九级的单元为基本单元,所占长度为1,第八级单元包含一个第九级单元,所占长度也为1,第七级单元包含2个八级单元,长度为2,第六级单元包含3个七级单元,长度为6,同理,第n级单元长度为(9-n)!
那么,问题来了,a[6][6][2][0][1][1][0][0][0]的地址是多少呢?这个简单,就是6*8!+6*7!+2*6!+0*5!+1*4!+1*3!+0*2!+0*1!+0*0!=273630,实际上,到这里我们就已经成功地将次序数列与这些整数一一对应起来了。
刚才我们说到过,在新的次序数列中,每一个数字确定了选门时门牌号剩下的数字中比它小的数字的个数,又因为剩下的每一个数字最后都会被使用,我们可以直观地将这个数列中的每一位数字理解为排列中对应数字右侧比其小的数字的个数。如783145269中7右侧比其小的数字有3,1,4,5,2,6,一共六个,8右侧也有六个比其小的数字,最终得到783145269对应的次序排列为662011000,同理,我们也可以根据次序数列662011000得到排列783145269(这个很好理解,这里我就不赘述了),然后根据上述方法,又将662011000与整数273630对应起来,并且这种对应也是唯一的。总的来看,我们就把排列783145269对应到了数字273630。
我们再引入一些术语:
在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。
如果初始的标准排序方式是从小到大,即123456789,那么783145269的逆序数就是6+6+2+1+1=16。
康托展开式的各项系数就是每个数位对应的逆序的个数(因为左小右大为正序,所以左大右小就是逆序)。现在再来看看康托展开式:
这个公式就构建了一个全排列与自然数的双射。