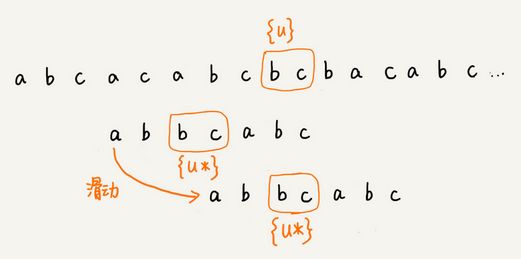1.基础数据结构类型
(1)线性结构
数组、链表、栈、队列
(2)非线性结构
树、图
2.数据结构变体
数组扩展:散列表(散列表用的是数组支持按照下标随机访问数据的特性)
链表扩展:跳表
树扩展:二叉树(二叉查找树、平衡二叉树、红黑树、堆)、Trie树
3.各种数据结构适用场景或算法应用
(1)数组
数组需要分配连续的内存空间,对内存有较大要求,但是可以利用CPU的缓存机制,查询执行速度快于链表。
(2)链表
不需要分配连续的内存空间,但需要保存指针。和数组相比,链表更适合插入、删除操作频繁的场景,查询的时间复杂度较高。
链表加多级索引的结构,就是跳表。跳表可以支持快速的插入、删除、查找。单链表插入、删除、查找一个数据时间复杂度是O(N),跳表能做到O(logN),相当于基于单链表实现了二分查找。
但比起链表要多O(N)的空间复杂度,不过索引结点只需要存储关键值和几个指针,并不需要存储对象。所以当存储对象比索引结点大很多时,索引占用的额外空间就可以忽略了。
(3)栈
特性
栈是后进先出、先进后出的。常见应用于函数调用。
实现方式
栈既可以用数组来实现,也可以用链表来实现。用数组实现的栈叫作顺序栈,用链表实现的栈叫作链式栈。
(4)队列
队列是“先进先出”的。
队列有基于链表(链式队列)和基于数组(顺序队列)这两种实现方式。
队列可以应用在线程池请求排队的场景,还可以应用在任何有限资源池中,用于排队请求,比如数据库连接池等。对于大部分资源有限的场景,当没有空闲资源时,基本上都可以通过“队列”这种数据结构来实现请求排队。
(5)树
①二叉树
二叉树重要的操作是前、中、后序遍历操作。二叉树中比较特殊的树是完全二叉树和满二叉树,满二叉树是完全二叉树的一种特殊情况。二叉树存储可以使用链式存储或者数组存储,完全二叉树适合使用数组存储。
二叉查找树是二叉树最常用的一种类型,支持快速查找。右子节点>树中的任意一个结点值>左子结点。极端情况下二叉查找树可能会退化成链表,时间复杂度会退化到 O(n)。
平衡二叉查找树可以解决复杂度退化问题。
AVL树符合平衡二叉查找树的严格定义,即任何节点的左右子树高度相差不超过 1,但AVL树维持平衡的成本很高。
红黑树是近似平衡,是一种不严格的平衡二叉查找树,在维护平衡的成本相对较低。在工程中更喜欢用红黑树而不是平衡二叉树。红黑树实现复杂,可以用跳表替代。
堆是完全二叉树,堆的重要应用有:优先级队列、求 Top K 和求中位数。
②Trie树
主要应用于多模式串匹配(在一个串中同时查找多个串),如搜索引擎。
扩展:AC自动机
(6)图
图的存储方式有邻接矩阵和邻接表。邻接矩阵存储比较浪费空间,特别是存储是稀疏图(顶点多,边少),但查询效率高,而且方便矩阵运算(如弗洛伊德算法)。邻接表的存储方式比较节省存储空间,但链表不方便查找,可以通过跳表、红黑树、散列表等提高查询效率。
可以应用于存储社交网络的好友关系。
图基本的搜索算法是广度优先搜索算法和深度优先搜索算法。
其他算法:拓扑排序
(7)散列表
①散列函数
散列函数可以算出数据存放对应的数组下标,当出现散列冲突可以通过开放寻址法(适合数据量比较小、装载因子小的时候)、链表法(适合存储大对象、大数据量的散列表。可以用红黑树代替链表来优化)来解决。
当散列表中空闲位置不多的时候,散列冲突的概率就会大大提高。为了保证散列表的操作效率,一般情况下会保证散列表有一定比例的空闲槽位。
②哈希算法
将任意长度的二进制值串映射为固定长度的二进制值串,这个映射的规则就是哈希算法,而通过原始数据映射之后得到的二进制值串就是哈希值。
哈希算法常见应用:
安全加密(MD5、SHA等)
唯一标识
对大数据做信息摘要,通过一个较短的二进制编码来表示很大的数据。数据校验
校验数据的完整性和正确性。如HTTPS中通过摘要算法保证数据的完整性散列函数
散列函数中用到的散列算法更加看重的是散列的平均性和哈希算法的执行效率负载均衡
通过哈希算法,对客户端 IP 地址或者会话 ID 计算哈希值,将取得的哈希值与服务器列表的大小进行取模运算,最终得到应该被路由到的服务器编号。
这样就可以把同一个 IP 过来的所有请求,都路由到同一个后端服务器上,实现会话粘滞(session sticky)。数据分片
通过哈希算法对数据分片,以实现采用多机分布式处理海量数据分布式存储
针对海量数据的缓存,可以通过哈希算法对数据取哈希值,然后对机器个数取模,得到应该存储的缓存机器编号。
这种方法有个缺点就是当扩容或缩容,所有的数据都要重新计算哈希值,然后重新搬移到正确的机器上。相当于缓存中的数据都失效了,可能发生雪崩效应,压垮数据库。可以采用一致性哈希算法来解决。
③散列表和二叉查找树比较
- 散列表插入、删除、查找的时间复杂度是O(1),而二叉查找树在比较平衡的基础上才能做到O(logN)。
- 但是散列表的数据是无序的,二叉查找树可以通过中序遍历在O(N)的时间复杂度内获得有序的数据。
- 散列表扩容耗时多,遇到散列冲突时,性能不稳定。平衡二叉树性能稳定,时间复杂度稳定在 O(logn)。
④为什么散列表经常和链表一起使用(如LinkedHashMap)?
- 散列表数据存储是无序的,无法支持按照某种顺序快速地遍历数据。如果希望按照顺序遍历散列表中的数据,需要将散列表中的数据拷贝到数组中,然后排序,再遍历。可以通过维护一个链表维持顺序,实现LRU淘汰算法。
- 借助散列表和双向链表可以实现O(1)的查询、删除操作
4.排序算法
(1)非线性排序算法
| 算法 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 是否原地排序 | 是否稳定 | 适用场景 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n) | O(n2) | O(n2) | 是 | 是 | 小规模数据排序 |
| 插入排序 | O(n) | O(n2) | O(n2) | 是 | 是 | 小规模数据排序 |
| 选择排序 | O(n2) | O(n2) | O(n2) | 是 | 否 | 小规模数据排序 |
| 快速排序 | O(nlogn) | O(n2) | O(nlogn) | 是 | 否 | 大规模数据排序 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | 否 | 是 | 大规模数据排序 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | 是 | 否 | 优先级队列、 Top K 、求中位数 |
ps:为了兼顾任意规模数据的排序,一般都会首选时间复杂度是 O(nlogn) 的排序算法来实现排序函数。
(2)线性排序算法
| 算法 | 时间复杂度 | 是否原地排序 | 是否稳定 | 排序数据要求 | 适用场景 |
|---|---|---|---|---|---|
| 桶排序 | O(n)(选择快排) | 否 | 是 | ①要排序的数据需要很容易就能划分成 m 个桶②数据在各个桶之间的分布是比较均匀的 | 外部排序 |
| 计数排序 | O(n+k) k是数据范围 | 否 | 是 | 非负整数 | 数据范围不大 |
| 基数排序 | O(dn) d是维度 | 否 | 是 | ①需要可以分割出独立的“位”来比较,而且位之间有递进的关系 ②位之间有递进的关系 ③每一位的数据范围不能太大,要可以用线性排序算法来排序 | 数据范围较大 |
ps:桶排序中时间复杂度、是否原地排序、是否稳定取决于桶内选取的排序算法;桶排序其实是一种算法思想;计数排序是一种特殊的桶排序
5.字符串匹配算法
(1)单模式串匹配(在一个主串中查找一个模式串)
①BF(Brute Force)算法
暴力匹配/朴素匹配算法。
思路:把主串的长度记作 n,模式串的长度记作 m。在主串中,检查起始位置分别是 0、1、2…n-m 且长度为 m 的 n-m+1 个子串,看有没有跟模式串匹配的。
时间复杂度:
最坏情况时间复杂度是 O(n*m)。
适用场景:
适合主串和模式串都不太长的情况。在实际的软件开发中,绝大部分情况下,朴素的字符串匹配算法就够用了。
②RK算法
RK 算法是借助哈希算法对 BF 算法进行改造。
思路:对主串中每个子串分别求哈希值,然后拿子串的哈希值与模式串的哈希值比较,减少了比较的时间。
时间复杂度:
O(n)。极端情况下,如果哈希算法存在大量的冲突,每次都要再对比子串和模式串本身,那时间复杂度就会退化成 O(n*m)。
适用场景:
字符集范围不要太大且模式串不要太长, 否则hash值可能冲突。但设计一个良好的哈希算法会比较困难。
③BM算法
借助“坏字符规则”和“好后缀规则”,在每一轮比较时,让模式串尽可能多移动几位,减少无谓的比较。
a.坏字符规则
从模式串的末尾往前倒着匹配,当发现某个字符没法匹配的时候。把这个没有匹配的字符叫作坏字符(主串中的字符)。
ps:坏字符的位置越靠右,下一轮模式串的挪动跨度就可能越长,节省的比较次数也就越多。这就是BM算法从右向左检测的好处。
把坏字符对应的模式串中的字符下标记作 si。如果坏字符在模式串中存在,把这个坏字符在模式串中的下标记作xi。如果不存在, xi 记作 -1。模式串往后移动的位数就等于 si-xi。如果坏字符在模式串里多处出现,选择最靠后的那个作为xi 。
时间复杂度:
利用坏字符规则,BM 算法最好时间复杂度是 O(n/m)。【 n是主串长度,m是模式串长度 】
单纯使用坏字符规则还是不够的。因为根据 si-xi 计算出来的移动位数,有可能是负数,比如主串是 aaaaaaaaaaaaaaaa,模式串是 baaa。不但不会向后滑动模式串,还有可能倒退。
b.好后缀规则
遇到无法匹配的坏字符后,看好后缀在模式串中,是否有另一个匹配的子串。如果有,则按如下滑动:
如果没有则从好后缀的后缀子串中,找一个最长的并且能跟模式串的前缀子串匹配的。
时间复杂度:
好后缀预处理最坏时间复杂度O(m * m),匹配O(n)【m是模式串长度,n是主串长度】
如何运用坏字符和好后缀规则?
分别计算好后缀和坏字符往后滑动的位数,然后取两个数中最大的,作为模式串往后滑动的位数。这种处理方法可以避免根据坏字符规则计算得到的往后滑动的位数有可能是负数的情况。
好后缀规则可以独立于坏字符规则使用。因为坏字符规则的实现比较耗内存,为了节省内存,可以只用好后缀规则来实现 BM 算法,但算法效率就会下降一些。
适用场景:
坏字符规则需要占用较多的空间,适合字符集不是很大的情况。
坏字符和好后缀都需要对模式串进行预处理,所以模式串最好不要太长。
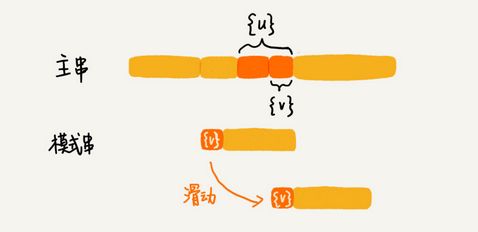
④KMP算法
KMP算法与BM算法类似,也是让模式串尽可能多移动几位,减少无谓的比较,KMP算法重点放在已匹配前缀上。
思路:在模式串和主串匹配的过程中,当遇到坏字符后,对于已经比对过的好前缀,在好前缀的后缀子串中,查找最长的那个可以跟好前缀的前缀子串匹配的。假设最长的可匹配的那部分前缀子串是{v},长度是 k。把模式串一次性往后滑动 j-k 位,相当于,每次遇到坏字符的时候,就把 j 更新为 k,i 不变,然后继续比较。
时间复杂度:
O(m+n)(其中构建next数组是O(m),借助next数组匹配是O(n))【m是模式串长度,n是主串长度】。
可结合小灰大牛这篇来食用:
漫画:什么是KMP算法?
(2)多模式串匹配(在一个主串中查找多个模式串)
①Trie 树
Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。
其中,根节点不包含任何信息。每个节点表示一个字符串中的字符,从根节点到红色节点的一条路径表示一个字符串(注意:红色节点并不都是叶子节点)。
时间复杂度:
构建 Trie 树的过程,需要扫描所有的字符串,时间复杂度是 O(n)【n 表示所有字符串的长度和 】。
构建好 Trie 树后,在其中查找字符串的时间复杂度是 O(k)【k 表示要查找的字符串的长度】。
空间复杂度:
空间复杂度取决于子节点存储大小。Trie 树有可能很浪费内存,为了解决内存问题,可以稍微牺牲一点查询的效率,将每个节点中的数组换成其他数据结构,来存储一个节点的子节点指针。比如有序数组、跳表、散列表、红黑树等。
适用场景:
精确匹配查找更适合用散列表或者红黑树来解决,Trie 树比较适合的是查找前缀匹配的字符串,适合多模式串公共前缀较多的匹配,如实现搜索关键词的提示功能。
②AC 自动机
AC 自动机实际上就是在 Trie 树之上,加了类似 KMP 的 next 数组,只不过此处的 next 数组是构建在树上。
时间复杂度:
构建Trie 树的时间复杂度是 O(m * len)【 len 表示敏感词的平均长度,m 表示敏感词的个数】。
失败指针的构建过程就是 O(k * len)【 k是 Trie 树中总的节点个数】。
AC 自动机做匹配的时间复杂度O(n * len),因为敏感词并不会很长,实际情况下,可能近似于 O(n)。【n是主串长度】
适用场景:
适合大量文本中多模式串的精确匹配查找,如敏感词过滤
6.二分查找
(1)特点
二分查找依赖的是顺序表结构,也就是数组,并且针对的是有序数据。时间复杂度为O(logN)。
(2)使用场景
①二分查找只能用在插入、删除操作不频繁,一次排序多次查找的场景中
②数据量太小不适合,此时使用顺序查找就足够了。数据量太大也不适合,二分查找的底层需要依赖数组这种数据结构,而数组为了支持随机访问的特性,要求内存空间连续,对内存的要求比较苛刻。
③如果数据之间的比较操作非常耗时,不管数据量大小,推荐使用二分查找。比如对于大字符串间的比较,可以尽量减少比较次数
7.其他算法思想
(1)贪心算法
贪心算法实际上是动态规划算法的一种特殊情况。针对一组数据,定义了限制值和期望值,希望从中选出几个数据,在满足限制值的情况下,期望值最大。
适用场景:
指导设计基础算法。比如Prim 和 Kruskal 最小生成树算法 、Dijkstra 单源最短路径算法、霍夫曼编码(Huffman Coding)(一种十分有效的编码方法,广泛用于数据压缩中)。
(2)分治算法
分治算法(divide and conquer)的核心思想是分而治之 ,也就是将原问题划分成 n 个规模较小,并且结构与原问题相似的子问题,递归地解决这些子问题,然后再合并其结果,就得到原问题的解。
分治算法一般都比较适合用递归来实现。
适用场景:
用来指导编码,降低问题求解的时间复杂度(如归并排序求逆序对)
解决海量数据处理问题。比如 MapReduce 本质上就是利用了分治思想。
(3)回溯算法
回溯相当于穷举搜索。穷举所有的解,找到满足期望的解。通过把问题求解的过程分为多个阶段。每个阶段,我们都会面对一个岔路口,我们先随意选一条路走,当发现这条路走不通的时候(不符合期望的解),就回退到上一个岔路口,另选一种走法继续走。
时间复杂度非常高,是指数级别的。
适用场景:
用来解决广义的搜索问题:从一组可能的解中,选择出一个满足要求的解。(如八皇后、0-1背包问题、正则表达式匹配等)
时间复杂度高,只能用来解决小规模数据的问题。
适合用递归来实现,在实现的过程中,剪枝操作是提高回溯效率的一种技巧。利用剪枝,我们并不需要穷举搜索所有的情况,从而提高搜索效率。
(4)动态规划
把问题分解为多个阶段,每个阶段对应一个决策。我们记录每一个阶段可达的状态集合(去掉重复的),然后通过当前阶段的状态集合,来推导下一个阶段的状态集合,动态地往前推进。
动态规划是一种空间换时间的算法思想。执行效率较回溯高,但是空间复杂度也高。
能解决的问题
符合一个模型,三个特征的问题。
- 一个模型
多阶段决策最优解模型。解决问题的过程,需要经历多个决策阶段。每个决策阶段都对应着一组状态。然后我们寻找一组决策序列,经过这组决策序列,能够产生最终期望求解的最优值。 - 三个特征
最优子结构:可以通过子问题的最优解,推导出问题的最优解。后面阶段的状态可以通过前面阶段的状态推导出来。
无后效性:在推导后面阶段的状态的时候,只关心前面阶段的状态值,不关心这个状态是怎么一步一步推导出来的;某阶段状态一旦确定,就不受之后阶段的决策影响。
重复子问题:不同的决策序列,到达某个相同的阶段时,可能会产生重复的状态
解题思路
- 状态转移表法:回溯算法实现 - 定义状态 - 画递归树 - 找重复子问题 - 画状态转移表 - 根据递推关系填表 - 将填表过程翻译成代码
- 状态转移方程法:找最优子结构 - 写状态转移方程 - 将状态转移方程翻译成代码
适用场景:
用来求解最优问题,比如求最大值、最小值等等。