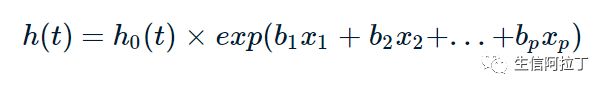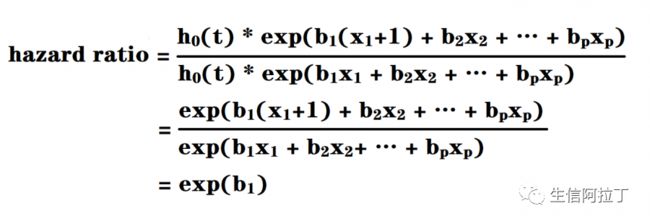作者:Resther
审稿:童蒙
编辑:angelica
在生物医学研究中,生存分析是非常重要和常见的分析方法。本文对生存分析中的Kaplan–Meier模型、Cox比例风险模型进行简要的介绍,帮助大家更好地理解生存分析等相关概念。
简介生存分析使用场景
生存分析经常用在癌症等疾病的研究中,例如在对某种抗癌药物做临床试验时,会首先筛选一部分癌症患者随机分为两组,一组服用该试验药物,一组服用对照药物,服药后开始统计每个患者从服药一直到死亡的生存时间,通过考察两组之间的病人在生存时间上是否有统计学差异来判断试验药物是否有效。
在这里,死亡是整个实验中重点观测的事件,即event。对于每个病人,需要记录他们发生该事件的具体时间。因此,生存分析可以抽象概述为,研究在不同条件下,特定事件发生与时间的关系是否存在差异。
这些具体事件可以是死亡,也可以是肿瘤转移、复发、病人出院、重新入院等任何可以明确识别的事件,而不同条件即为不同的分组依据,可以是年龄、性别、地域、某个基因表达量的高低、某个突变的携带与否等等。
Kaplan–Meier方法
一、方法介绍
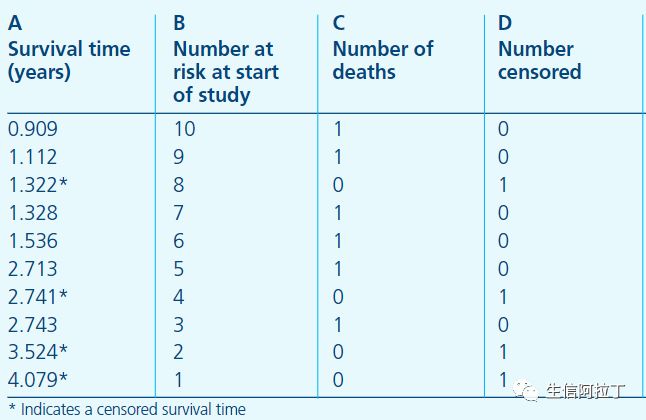
该方法是由Kaplan和Meier于1958年共同提出的。我们首先通过一个例子对该方法进行理解:A列是从试验开始起,持续的观测时间,星号代表在该时间有删失数据发生;
B列是指在A列对应的时间开始之前所有存活的研究对象个数,也可以叫做at risk的人数,表示当前具有死亡风险的有效人群,是排除了已经死亡和删失的数据之后剩余的人数;
C列为恰好在A列对应的时间死亡的人数;
D列是在该时间点删失的个数,即在实验过程中丢失的、失去跟踪的数据。
在引入Kaplan–Meier公式之前,大家可以先尝试自己去思考下如何计算每个时间节点的生存概率,即研究对象从试验开始直到某个特定时间点仍然存活的概率S(t)。比如在1.536年这个时间点,即表中的第五行,病人在该点的生存概率是多少呢?
很容易可以想到,要想在1.536这个时间点存活,他/她必须在1.536之前的所有时间点存活才行,也就是说在0.909、1.112、1.322、1.328这几个时间点,病人都必须存活。那么在1.536这个时间点的生存概率实际上就等于在包括1.536 在内的所有之前的时间点都不死亡的概率乘积,即:P(存活至1.536) = P(0.909时不死亡) * P(1.112时不死亡) * P(1.322时不死亡) * P(1.328时不死亡) * P(1.536时不死亡)
对于某个特定时间点不死亡的概率,可以用 1 – 死亡概率 来估算,举个例子:P(0.909时不死亡) = 1 – P(0.909时死亡) = 1 – (0.909时死亡的人数)/(0.909之前的所有人数) = 1 – 1/10 = 0.9
当我们计算出每个时间点不死亡的概率之后,我们就可以通过连续乘积算出每个时间点的生存概率,即存活至该时间点的概率。如下表所示:
该表中E列即不死亡概率,F列则表示累积的生存概率,可以看到随着时间增加,死亡人数增多,越到后期,生存概率越低。
二、方法思路
上面这个例子的思路就是Kaplan–Meier方法的主要思路,我们也可以用数学公式来表示。一共有m个时间点,每个时间点用下标 i 来表示, i 为从 1 到 m 的整数, 生存概率 S(ti) 可以表示为:
其中,ti 表示第 i 个时间点,ni 表示在 ti 之前的有效人数,di 表示在 ti 死亡的人数,S(ti-1) 表示在上一个时间点 i-1 的生存概率。
根据这一公式,我们可以画图来展示生存率的变化情况,即Kaplan-Meier生存曲线,如下图所示:
图中横轴即时间轴,纵轴是累积存活比例,也就是生存概率,加号表示删失数据。
三、差异检验
一般来说,生存分析是要比较不同组之间的一个生存情况,因此Kaplan-Meier生存曲线一般不止一条曲线。如果想比较整体生存时间分布是否存在统计学差异,一般我们可以采用Logrank统计方法来对生存数据进行统计分析。Logrank统计方法假设两组的生存时间分布一致,去检验是否能拒绝该假设。
除了Logrank检验之外,常用的检验包括Breslow检验,即Wilcoxon检验。该方法加入了权重因子,即每个时刻的总人数,使得试验前期的权重较大,贡献更大,所以Breslow检验对试验前期的差异更加敏感。
Cox模型
一、方法说明
Kaplan-Meier方法只能针对单一的变量进行分析,无法同时考察多个因素。当需要同时考察多个因素的影响时,这时我们可以使用Cox比例风险回归模型。
Cox比例风险回归模型(Cox's proportional hazards regression model),简称Cox模型,Cox来自提出者英国统计学家D.R.Cox的名字,主要用于肿瘤和其他疾病的预后分析。这个模型是一种半参数回归模型,因为它的公式中既包含参数模型又包含非参数模型。
其中
t是生存时间,
x1, x2到xp指的是具有预测效应的多个变量,
b1,b2到bp则是每个变量对应的effect size,即效应量,可以理解为结果的影响程度。
h(t)就是不同时间t的 hazard,即风险值,例如在观测死亡事件时,指的是研究对象从试验开始到某个特定时间t之前存活,但在t时间点发生死亡的概率。
h0(t)是基准风险函数,也就是说在其他协变量x1, x2到xp都为0时,即不起作用时,衡量风险值的函数。
根据公式我们可以看到指数部分是参数模型,因为其参数个数有限,即b1,b2到bp,而基准风险函数h0(t)由于于其未确定性,可根据不同数据来使用不同的分布模型,因此是非参数模型。所以说, Cox模型是一种半参数模型。
从公式中我们可以看到,Cox模型能够把诸多可能影响生存率的因素都当作协变量引入到公式中去,在该公式中即x1, x2到xp,所以可以同时考察多个因素的影响。
我们的主要目标是通过一定方法来找到合适的h0(t),以及所有协变量的系数b1,b2到bp。实际上cox模型是需要用到极大似然估计等计算方法,首先构建特定的似然函数,通过梯度下降等方法来求解模型的参数,使得函数求解值最大,这里不对细节进行解读。
假设我们已经通过计算得到了合适的h0(t)和协变量系数,如何去解读结果呢?我们可以比较某个协变量x1 在不同值时对应的不同风险比(hazard ratio),这里 x1和x1+1,即若增加1个单位,增加前后的风险比实际上等于 exp(b1)。
假如x1指的是年龄,那么对于年龄 51岁 (x+1) 和年龄 50 岁 (x) 的人,可能死亡的风险比为 exp(b1)。如果b1>0,则 exp(b1)>1,意味着年龄+1,死亡风险增加;如果b1<0, 则 exp(b1)<1,意味着年龄+1,死亡风险降低;如果b1=0,exp(b1)=1,意味着年龄变化对死亡风险不起作用。从hazard ratio推导的结果看到,它是不包括时间t的。这是Cox模型可用的一个基本假设,即任意两人的风险比例是不随时间变化的。
二、计算与解读
研究者开发了方便进行生存分析的R包,survival和survminer。首先安装并加载这两个包:
install.packages(c("survival","survminer"))
library("survival")
library("survminer")
在survival包中提供了coxph()函数可以用来计算cox模型:
coxph(formula, data, method)
method默认为 “efron”,也可以是 “breslow”和“exact” 。以示例数据为例:
data("lung")
res.cox <- coxph(Surv(time, status) ~ sex, data = lung)
summary(res.cox)
Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)
n= 228, number of events= 165
coef exp(coef) se(coef) z Pr(>|z|)
sex -0.5310 0.5880 0.1672 -3.176 0.00149 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
exp(coef) exp(-coef) lower .95 upper .95
sex 0.588 1.701 0.4237 0.816
Concordance= 0.579 (se = 0.022 )
Rsquare= 0.046 (max possible= 0.999 )
Likelihood ratio test= 10.63 on 1 df, p=0.001111
Wald test = 10.09 on 1 df, p=0.001491
Score (logrank) test = 10.33 on 1 df, p=0.001312
从结果中看到:sex对应的系数(coef)为-0.5310,小于0表示sex增加会降低风险,风险比(hazard ratio)为exp(coef) =0.588,该数值小于1,同样表明sex增加会导致风险增加,即女性比男性预后更好。
除了关注系数外,同时需要关注的是p value,即该参数估计是否具有统计学显著性,这里给出三种方法的结果,分别是Likelihood ratio test,Wald test和Score logrank test。
分析多个因素的影响:
res.cox <- coxph(Surv(time, status) ~ age+sex+ph.ecog, data = lung)
summary(res.cox)
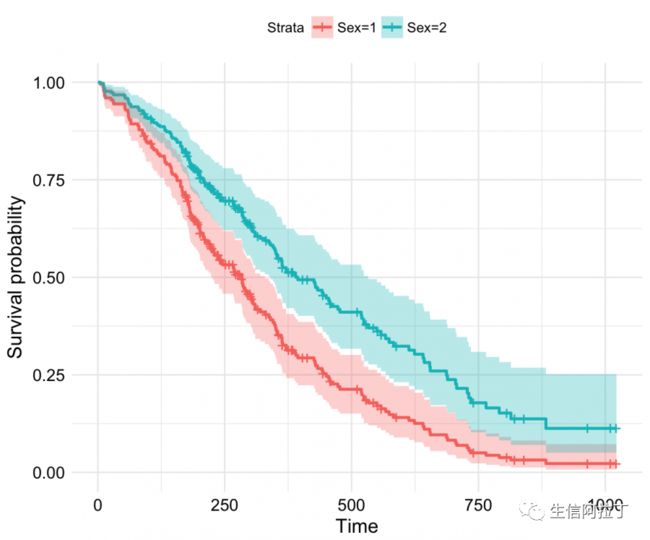
最后是结果的可视化:
fit <- survfit(res.cox, data = lung)
ggsurvplot(fit, conf.int = TRUE, legend.labs=c("Sex=1", "Sex=2"),
ggtheme = theme_minimal())
以上是对生存分析中主要知识的一个整理,希望梳理清楚生存分析中的大多数概念,有助于大家在自己的工作中使用相关方法进行分析。