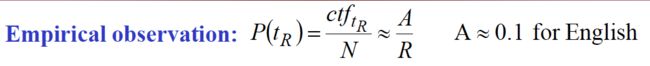Bag of Words
解释:
搜素引擎用词袋模型这种shallow form理解语言。词袋模型的特征有:
1)忽略word order;
2)忽略stopwords(像the,a这种频率高又没什么实际意义的词);
3)把words变成terms,将root相同的words变成一个term,比如cats->cat
优缺点:
pros:简单;有效
cons:有损的,无法从词袋还原到原文档;忽略了词句篇的语义信息
Language-independent properties
def: 与词汇特征、词形、语法等无关的特性。(? not sure)
example
以华尔街日报为例:
term frequency的分布非常skewed:频繁出现的terms很少,很多都是罕见的terms。
这个分布的样式与人类使用语言的习惯有关,不同的语言和corpus中,曲线的斜率和具体词汇的排名和频率会发生变化。
Heaps' Law
描述vocabulary大小(total number of terms)和总词数(total number of word occurrences)的关系。
根据Heapf‘s Law,vocabulary的大小会一直随着word occurrences总数的增长而增长,虽然越来越慢,但不会饱和。
Zipf’s Law
描述collection term frequency和term‘s rank的关系。
ctf: collection term frequency -- how often term t occurs in C
N: total word occurrences in corpus C
A: constant, usually 0.1 for English
R: rank of term t
不需要知道collection里含有多少文章,文章的具体内容就能得到ctf和rank的关系。
由Zipf‘s Law可知:
1)few term频繁出现:
rank 1的term占总word occurrence的10%;
排名前5的terms占有23%的occurrences;
排名前100的terms占有52%的occurrences
2)大多数terms非常罕见:
50%的terms出现1次;
91%的terms的occurrence小于10次
Heapf's Law 和Zipf's Law的作用
1)帮助系统设计者预计重要data structure(term dictionary,inverted list 的大小的分布情况)需要占用的内存大小。这些预计无需了解corpus中具体的内容和语言,非常的方便。
2)根据这些统计特性,帮助设计者更好得设计data structure(比如把doc-term矩阵换成了inverted list)。
3)不同inverted lists之间,大小变化很大:
rank 1的term的inverted list含有10%的总term occurrences;
vocabulary中,50%的term的inverted list只有一个occurrence;
83%的term的inverted list记录的出现次数小于5;
所以软件应该能hold住对不同大小的inverted list的处理。
![[笔记] Introduction to Shallow Language Processing_第1张图片](http://img.e-com-net.com/image/info10/7f8f331232ab4c52ba653bb9c5615feb.jpg)
![[笔记] Introduction to Shallow Language Processing_第2张图片](http://img.e-com-net.com/image/info10/9eedfb9b51d74feba7b5a500bd124417.jpg)