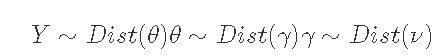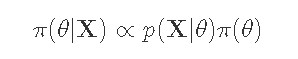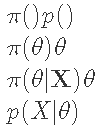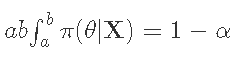原文链接:http://tecdat.cn/?p=23236
什么是频率学派?
在频率学派中,观察样本是随机的,而参数是固定的、未知的数量。
概率被解释为一个随机过程的许多观测的预期频率。
有一种想法是 "真实的",例如,在预测鱼的生活环境时,盐度和温度之间的相互作用有一个回归系数?
什么是贝叶斯学派?
在贝叶斯方法中,概率被解释为对信念的主观衡量。
所有的变量--因变量、参数和假设都是随机变量。我们用数据来确定一个估计的确定性(可信度)。
这种盐度X温度的相互作用反映的不是绝对的,而是我们对鱼的生活环境所了解的东西(本质上是草率的)。
目标
频率学派
保证正确的误差概率,同时考虑到抽样、样本大小和模型。
- 缺点:需要对置信区间、第一类和第二类错误进行复杂的解释。
- 优点:更具有内在的 "客观性 "和逻辑上的一致性。
贝叶斯学派
分析更多的信息能在多大程度上提高我们对一个系统的认识。
- 缺点:这都是关于信仰的问题! ...有重大影响。
- 优点: 更直观的解释和实施,例如,这是这个假设的概率,这是这个参数等于这个值的概率。可能更接近于人类自然地解释世界的方式。
实际应用中:为什么用贝叶斯
- 具有有限数据的复杂模型,例如层次模型,其中
- 实际的先验知识非常少
贝叶斯法则:
一些典型的贝叶斯速记法。
注意:
- 贝叶斯的最大问题在于确定先验分布。先验应该是什么?它有什么影响?
目标:
计算参数的后验分布:π(θ|X)。
点估计是后验的平均值。
一个可信的区间是
你可以把它解释为一个参数在这个区间内的概率 。
计算
皮埃尔-西蒙-拉普拉斯(1749-1827)(见:Sharon Bertsch McGrayne: The Theory That Would Not Die)
- 有些问题是可分析的,例如二项式似然-贝塔先验。
- 但如果你有很多参数,这是不可能完成的操作
- 如果你有几个参数,而且是奇数分布,你可以用数值乘以/整合先验和似然(又称网格近似)。
- 尽管该理论可以追溯到1700年,甚至它对推理的解释也可以追溯到19世纪初,但它一直难以更广泛地实施,直到马尔科夫链蒙特卡洛技术的发展。
MCMC
MCMC的思想是对参数值θi进行 "抽样"。
回顾一下,马尔科夫链是一个随机过程,它只取决于它的前一个状态,而且(如果是遍历的),会生成一个平稳的分布。
技巧 "是找到渐进地接近正确分布的抽样规则(MCMC算法)。
有几种这样的(相关)算法。
- Metropolis-Hastings抽样
- Gibbs 抽样
- No U-Turn Sampling (NUTS)
- Reversible Jump
一个不断发展的文献和工作体系!
Metropolis-Hastings 算法
Metropolis-Hastings: 硬币例子
你抛出了5个正面。你对θ的最初 "猜测 "是
MCMC:
p.old <- prior *likelihood
while(length(thetas) <= n){
theta.new <- theta + rnorm(1,0,0.05)
p.new <- prior *likelihood
if(p.new > p.old | runif(1) < p.new/p.old){
theta <- theta.new
p.old <- p.new
}画图:
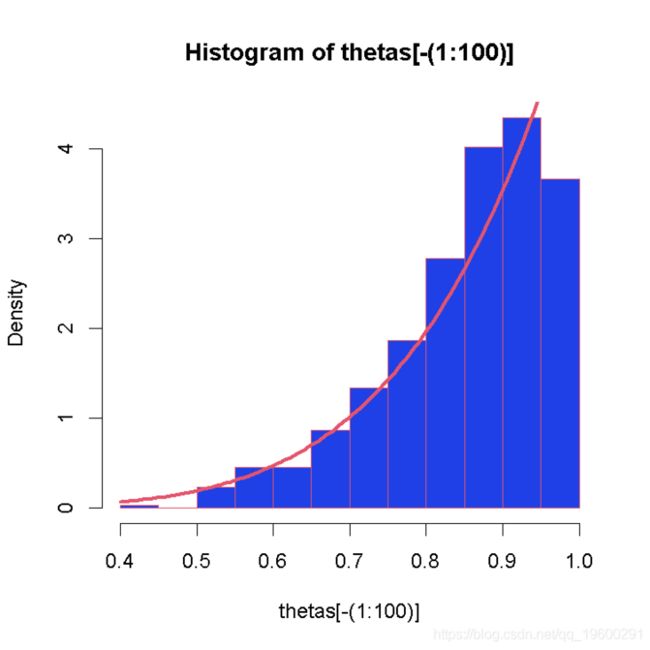
hist(thetas\[-(1:100)\] )
curve(6*x^5 )采样链:调整、细化、多链
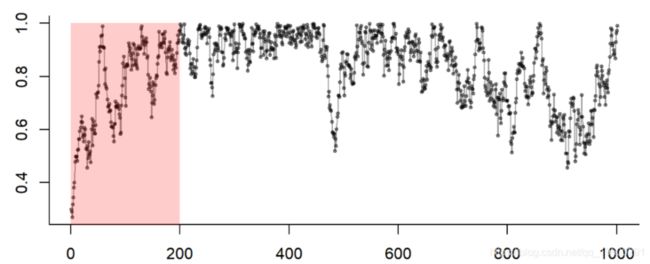
- 那个 "朝向 "平稳的初始过渡被称为 "预烧期",必须加以修整。
- 怎么做?用眼睛看
- 采样过程(显然)是自相关的。
- 如何做?通常是用眼看,用acf()作为指导。
- 为了保证你收敛到正确的分布,你通常会从不同的位置获得多条链(例如4条)。
- 有效样本量
MCMC 诊断法
R软件包帮助分析MCMC链。一个例子是线性回归的贝叶斯拟合(α,β,σ
plot(line)预烧部分:
plot(line\[\[1\]\], start=10)MCMC诊断法
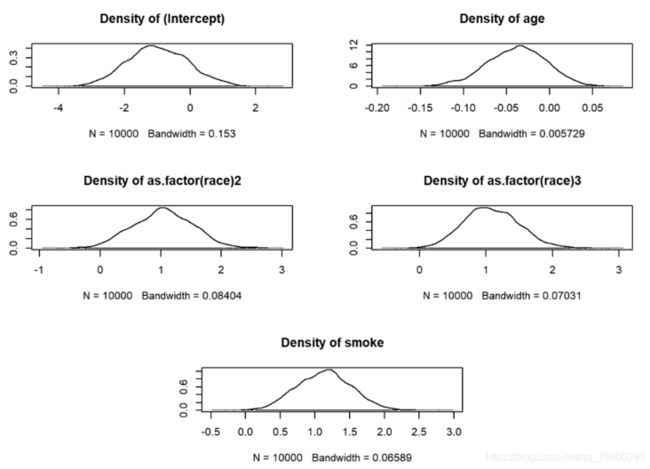
查看后验分布(同时评估收敛性)。
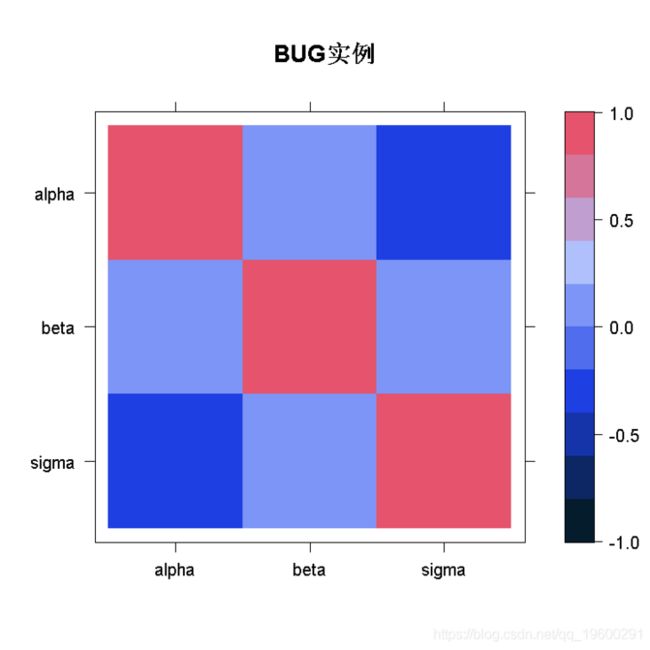
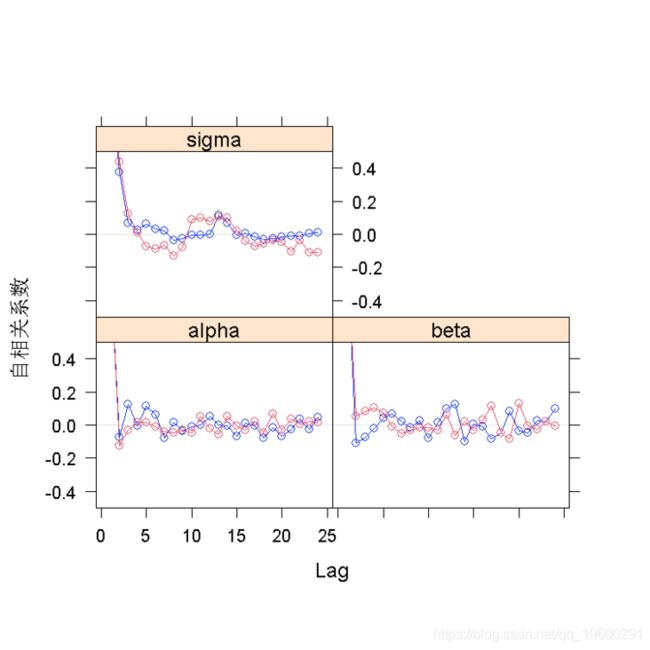
density(line)参数之间的关联性,以及链内的自相关关系
levelplot(line\[\[2\]\])
acfplot(line)统计摘要
运行MCMC的工具(在R内部)
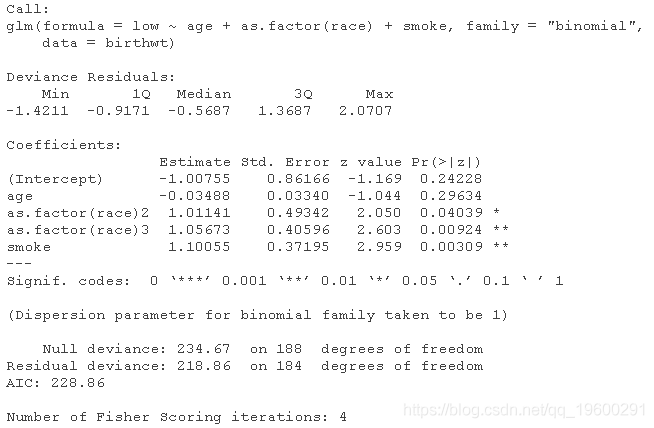
逻辑Logistic回归:婴儿出生体重低
logitmcmc(low~age+as.factor(race)+smoke )plot(mcmc)MCMC与GLM逻辑回归的比较
MCMC与GLM逻辑回归的比较
对于这个应用,没有很好的理由使用贝叶斯建模,除非--你是 "贝叶斯主义者"。 你有关于回归系数的真正先验信息(这基本上是不太可能的)。
一个主要的缺点是 先验分布棘手的调整参数。
但是,MCMC可以拟合的一些更复杂的模型(例如,层次的logit MCMChlogit)。
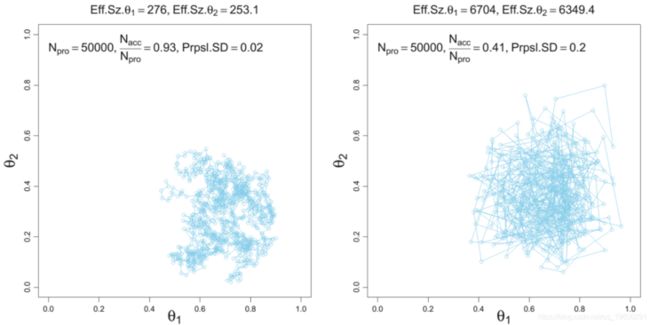
Metropolis-Hastings
Metropolis-Hastings很好,很简单,很普遍。但是对循环次数很敏感。而且可能太慢,因为它最终会拒绝大量的循环。
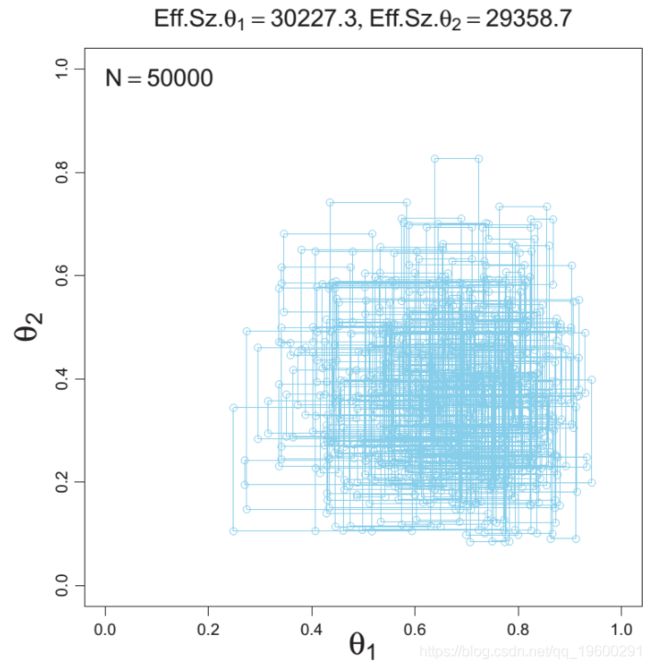
Gibbs 采样
在Gibbs吉布斯抽样中,你不是用适当的概率接受/拒绝,而是用适当的条件概率在参数空间中行进。 并从该分布中抽取一次。
然后你从新的条件分布中抽取下一个参数。
比Metropolis-Hastings快得多。有效样本量要高得多!
BUGS(OpenBUGS,WinBUGS)是使用吉布斯采样器的贝叶斯推理。
JAGS是 "吉布斯采样器"
其他采样器
汉密尔顿蒙特卡洛(HMC)--是一种梯度的Metropolis-Hastings,因此速度更快,对参数之间的关联性更好。
No-U Turn Sampler(NUTS)--由于不需要固定的长度,它的速度更快。这是STAN使用的方法(见http://arxiv.org/pdf/1111.424...)。
(Hoffman and Gelman 2011)
其他工具
你可能想创建你自己的模型,使用贝叶斯MC进行拟合,而不是依赖现有的模型。为此,有几个工具可以选择。
- BUGS / WinBUGS / OpenBUGS (Bayesian inference Using Gibbs Sampling) - 贝叶斯抽样工具的鼻祖(自1989年起)。WinBUGS是专有的。OpenBUGS的支持率很低。
- JAGS(Just Another Gibbs Sampler)接受一个用类似于R语言的语法编写的模型字符串,并使用吉布斯抽样从这个模型中编译和生成MCMC样本。可以在R中使用rjags包。
- Stan(以Stanislaw Ulam命名)是一个类似于JAGS的相当新的程序--速度更快,更强大,发展迅速。从伪R/C语法生成C++代码。安装:http://mc-stan.org/rstan.html**
- Laplace’s Demon 所有的贝叶斯工具都在R中: http://www.bayesian-inference...
STAN
要用STAN拟合一个模型,步骤是:
- 为模型生成一个STAN语法伪代码(在JAGS和BUGS中相同
- 运行一个R命令,用C++语言编译该模型
- 使用生成的函数来拟合你的数据
STAN示例--线性回归
STAN代码是R(例如,具有分布函数)和C(即你必须声明你的变量)之间的一种混合。每个模型定义都有三个块。
_1_.数据块:
int n; //
vector\[n\] y; // Y 向量这指定了你要输入的原始数据。在本例中,只有Y和X,它们都是长度为n的(数字)向量,是一个不能小于0的整数。
_2_. 参数块
real beta1; // slope这些列出了你要估计的参数:截距、斜率和方差。
_3_. 模型块
sigma ~ inv_gamma(0.001, 0.001);
yhat\[i\] <- beta0 + beta1 * (x\[i\] - mean(x));}
y ~ normal(yhat, sigma);注意:
- 你可以矢量化,但循环也同样快
- 有许多分布(和 "平均值 "等函数)可用
请经常参阅手册! https://github.com/stan-dev/stan/releases/download/v2.9.0/stan-reference-2.9.0.pdf
2. 在R中编译模型
你把你的模型保存在一个单独的文件中, 然后用stan_model()命令编译这个模型。
这个命令是把你描述的模型,用C++编码和编译一个NUTS采样器。相信我,自己编写C++代码是一件非常非常痛苦的事情(如果没有很多经验的话),而且它保证比R中的同等代码快得多。
注意:这一步可能会很慢。
3. 在R中运行该模型
这里的关键函数是sampling()。还要注意的是,为了给你的模型提供数据,它必须是列表的形式
模拟一些数据。
X <- runif(100,0,20)
Y <- rnorm(100, beta0+beta1*X, sigma)进行取样!
sampling(stan, Data)这里有大量的输出,因为它计算了
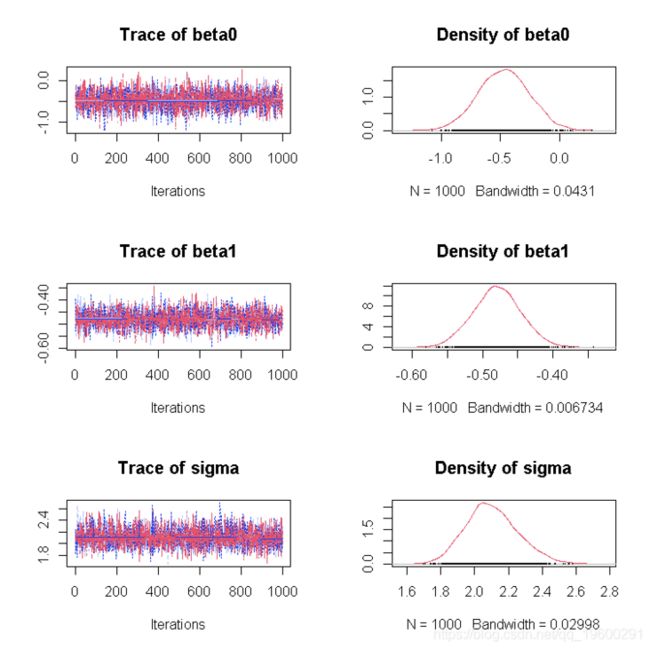
print(fit, digits = 2)MCMC诊断法
为了应用coda系列的诊断工具,你需要从STAN拟合对象中提取链,并将其重新创建为mcmc.list。
extract(stan.fit
alply(chains, 2, mcmc)最受欢迎的见解
4.R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归