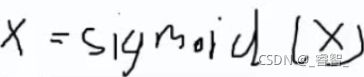深度学习(5)构造简单的神经网络
目录
一、激励函数
二、创建数组(初始输入和输出)
三、更新权重
1、创建权重(w0和w1)
2、限值(-1~1)
3、正向传播
4、反向传播
4-1、求l2差错
4-2、求l1差错
五、更新权重
总代码
一、激励函数
# 激励函数
def Sigmoid(x, deriv = False):
# 反向传播
if deriv == True:
return x*(x-1) #求导
# 正向传播
else:
return 1/(1+np.exp(-x)) #1/[1+e^(-x)]二、创建数组(初始输入和输出)
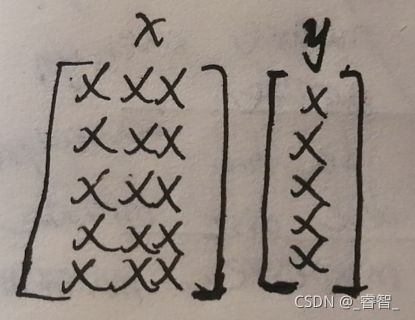
# 创建数组(输入参数、标签)
x, y = Create_Array()# 创建数组(输入和标签)
def Create_Array():
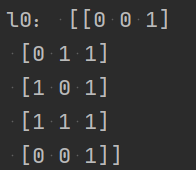
# 输入
# (这里有5个数据,3个特征)
x = np.array([
[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1],
[0, 0, 1]
])
print(x.shape)
# 标签(类别标签)
# 这里有5个标签(对应5个数据),共2种标签
y = np.array([
[0],
[1],
[1],
[0],
[0]
])
print(y.shape)
return x,y三、更新权重
1、创建权重(w0和w1)
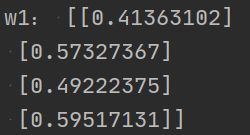
# 1、创建w0和w1
w0 = np.random.random((3, 4)) #3:输入特征有3个 4:神经元数量
w1 = np.random.random((4, 1)) #4:输入特征4个 1:神经元数量(输出特征)可以看出来它的取值在0~1,我们想把它限制在-1~1。
2、限值(-1~1)
# 2、限值在-1~1(本来是0~1)
w0 = w0 * 2 - 1
w1 = w1 * 2 - 13、正向传播
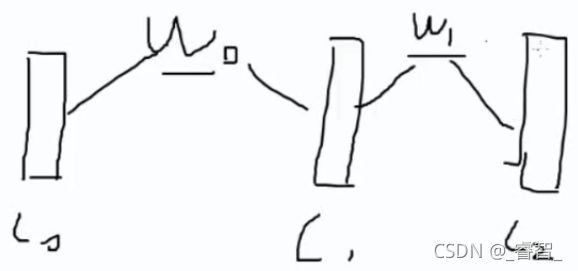
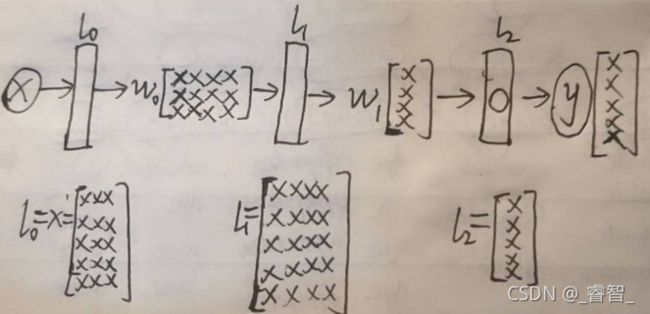
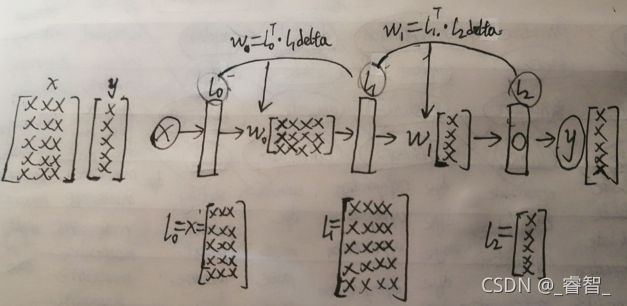
矩阵:例如w0[3,4],可以理解为:前面输入为3,后面输出为4。
# 3、正向传播
l0 = x #输入层(第一层)
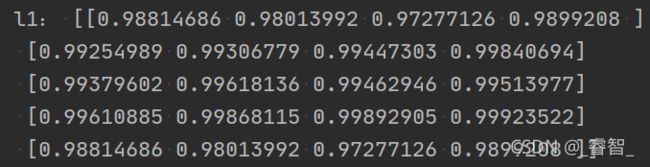
l1 = Sigmoid(np.dot(l0, w0)) #中间层(第二层)
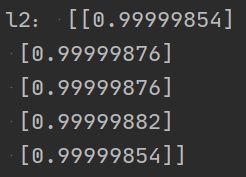
l2 = Sigmoid(np.dot(l1, w1)) #输出层(第三层)4、反向传播
矩阵:例如w0[3,4],可以理解为:前面输入为3,后面输出为4。
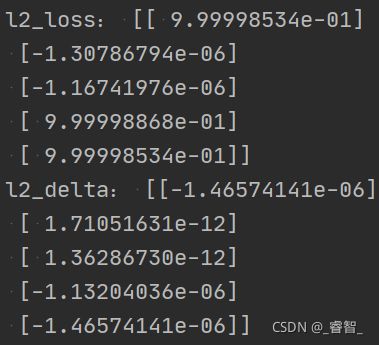
4-1、求l2差错
l2误差 = l2值 - 预期值
# l2
l2_loss = l2 - y # l2误差(损失)(预测值和真实值的差)
l2_delta = l2_loss * Sigmoid(l2, deriv=True) # l2每个样本错了多少4-2、求l1差错
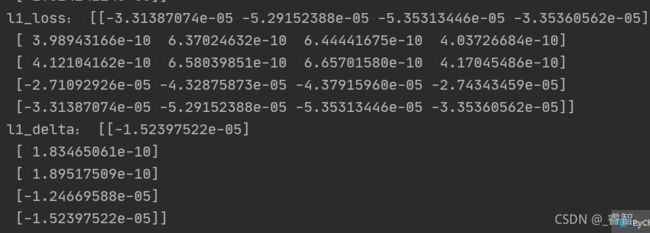
l1误差 = l2误差 * w1转置
# l1
l1_loss = l2_delta.dot(w1.T) # l1误差(损失)(l2差错矩阵*w1转置)
l1_delta = l2_loss * Sigmoid(l2, deriv=True) # l1每个样本错了多少五、更新权重
w1 -= l1转置 * l2差错
w0 -= l0转置 * l1差错
# 5、更新权重:w1和w0
w1 -= l1.T.dot(l2_delta)
w0 -= l0.T.dot(l1_delta)#每10000次打印一次(观察优化效果)
if i%10000 == 0:
print('w1:', w1)
print('w0', w0)
print('---------------------------------------------')观察优化效果:
误差: [[ 0.32966685]
[-0.67656896]
[-0.66531841]
[ 0.32919543]
[ 0.32966685]]
w1: [[ 0.12175521]
[-0.31912182]
[-0.25200495]
[-0.81755089]]
w0 [[-0.92863401 0.44797085 -0.13338118 -0.47594584]
[ 0.18454401 0.58964472 0.20720542 -0.15294761]
[-0.75583748 -0.05354275 0.88698458 0.44581214]]
---------------------------------------------
误差: [[ 9.99991933e-01]
[-7.32072362e-06]
[-9.10900613e-06]
[ 9.99991930e-01]
[ 9.99991933e-01]]
w1: [[2.69487986]
[2.64026488]
[3.62495426]
[3.06034898]]
w0 [[-0.74974059 0.62686427 0.04551225 -0.29705242]
[ 0.40014002 0.80524073 0.42280143 0.0626484 ]
[ 2.92079498 3.62308971 4.56361704 4.1224446 ]]
---------------------------------------------
误差: [[ 9.99995932e-01]
[-3.69171529e-06]
[-4.46189795e-06]
[ 9.99996035e-01]
[ 9.99995932e-01]]
w1: [[2.85382632]
[2.80498355]
[3.79129229]
[3.22544424]]
w0 [[-0.69432892 0.68227594 0.10092392 -0.24164074]
[ 0.45555183 0.86065254 0.47821324 0.11806021]
[ 3.08851435 3.79080908 4.73133641 4.29016397]]
---------------------------------------------
误差: [[ 9.99997276e-01]
[-2.47455531e-06]
[-2.94423290e-06]
[ 9.99997376e-01]
[ 9.99997276e-01]]
w1: [[2.94760072]
[2.90159829]
[3.88874508]
[3.3222891 ]]
w0 [[-0.66229777 0.71430709 0.13295506 -0.2096096 ]
[ 0.48758301 0.89268372 0.51024442 0.15009139]
[ 3.18666302 3.88895776 4.82948508 4.38831264]]
---------------------------------------------
误差: [[ 9.99997951e-01]
[-1.86322517e-06]
[-2.19361346e-06]
[ 9.99998039e-01]
[ 9.99997951e-01]]
w1: [[3.01447732]
[2.97028531]
[3.95798219]
[3.39113988]]
w0 [[-0.63969395 0.73691091 0.15555889 -0.18700578]
[ 0.51018686 0.91528756 0.53284826 0.17269523]
[ 3.25635009 3.95864483 4.89917215 4.45799971]]
---------------------------------------------
误差: [[ 9.99998358e-01]
[-1.49514816e-06]
[-1.74651365e-06]
[ 9.99998435e-01]
[ 9.99998358e-01]]
w1: [[3.06653951]
[3.02364596]
[4.01174561]
[3.44462675]]
w0 [[-0.62221616 0.7543887 0.17303668 -0.16952798]
[ 0.52766466 0.93276537 0.55032607 0.19017304]
[ 3.31043959 4.01273433 4.95326165 4.51208921]]可以发现误差在不断减小,说明我们的神经网络优化起了效果。
总代码
# 简单的神经网络
import numpy as np
# 激励函数
def Sigmoid(x, deriv = False):
# 反向传播
if deriv == True:
return x*(x-1) #求导
# 正向传播
else:
return 1/(1+np.exp(-x)) #1/[1+e^(-x)]
# 创建数组(输入和标签)
def Create_Array():
# 输入
# (这里有5个数据,3个特征)
x = np.array([
[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1],
[0, 0, 1]
])
print(x.shape)
# 标签(类别标签)
# 这里有5个标签(对应5个数据),共2种标签
y = np.array([
[0],
[1],
[1],
[0],
[0]
])
print(y.shape)
return x,y
# 更新权重
def Update_Weight(x, y):
# 1、创建w0和w1
w0 = np.random.random((3, 4)) #3:输入特征有3个 4:神经元数量
w1 = np.random.random((4, 1)) #4:输入特征4个 1:神经元数量(输出特征)
# 2、限值在-1~1(本来是0~1)
w0 = w0 * 2 - 1
w1 = w1 * 2 - 1
# 遍历
for i in range(60000):
# 3、正向传播
l0 = x #输入层(第一层)
l1 = Sigmoid(np.dot(l0, w0)) #中间层(第二层)
l2 = Sigmoid(np.dot(l1, w1)) #输出层(第三层)
# 4、反向传播
# l2
l2_loss = l2 - y # l2误差(损失)(预测值和真实值的差)
l2_delta = l2_loss * Sigmoid(l2, deriv=True) # l2每个样本错了多少
# l1
l1_loss = l2_delta.dot(w1.T) # l1误差(损失)(l2差错矩阵*w1转置)
l1_delta = l2_loss * Sigmoid(l2, deriv=True) # l1每个样本错了多少
# 5、更新权重:w1和w0
w1 -= l1.T.dot(l2_delta)
w0 -= l0.T.dot(l1_delta)
#每10000次打印一次(观察优化效果)
if i%10000 == 0:
print('误差:', l2_loss)
print('w1:', w1)
print('w0', w0)
print('---------------------------------------------')
if __name__ == '__main__':
# 创建数组(输入参数、标签)
x, y = Create_Array()
# 更新权重
Update_Weight(x, y)以后深度学习,一般不会自己写,一般都是用别人写好的框架,比如caffe、tensorflow等等框架。