树状数组和线段树快速应用

树状数组

树状数组的下标要从1开始

树状数组(Olog(n))

• 单点修改(修改原数组A的某一个值，对应的前缀和数组C也会快速更新)
• 区间查询(查询任意区间之和)

本文针对树状数组以单点修改和区间查询展开应用

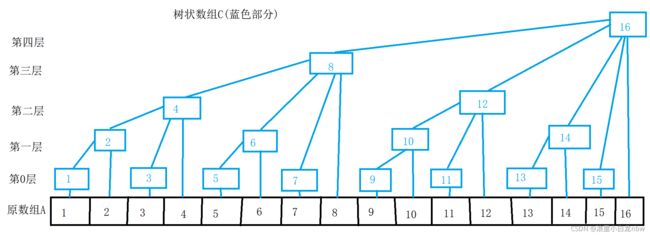
什么是树状数组？(图片举例)

相关解释：

1. 数组A的值为1-16（下标从1开始）
2. C[x]表示数组c的第x个元素
3. 如图所示C[x]中下标x为奇数时，全在第0层，如C[1]、C[3]…
4. C[x]所在层数为x二进制末尾有几个0，有几个0就在第几层
5. x的父节点下标是x+lowbit(x)，lowbit(x)= x & -x,即lowbit(x)=2的k次方,k为x二进制末尾0的个数。
6. c[x]的值为原数组a(x-2的k次方(lowbit(x)),x]之间的和（k为x的二进制末尾0的个数)

快速应用

模板题

动态求连续区间和
给定 n 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 [a,b] 的连续和。

输入格式
第一行包含两个整数 n 和 m，分别表示数的个数和操作次数。

第二行包含 n 个整数，表示完整数列。

接下来 m 行，每行包含三个整数 k,a,b （k=0，表示求子数列[a,b]的和；k=1，表示第 a 个数加 b）。

数列从 1 开始计数。

输出格式
输出若干行数字，表示 k=0 时，对应的子数列 [a,b] 的连续和。

数据范围
1≤n≤100000,
1≤m≤100000，
1≤a≤b≤n,
数据保证在任何时候，数列中所有元素之和均在 int 范围内。

输入样例：

10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8

输出样例：

11
30
35

代码如下：

#include 
#include 
#include 
#include 

using namespace std;

const int N = 100010;

int n, m;
int a[N], tr[N];//定义原数组和树状数组

int lowbit(int x)
{
     
    return x & -x;
}

void add(int x, int v)//单点修改
{
     
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}

int query(int x)//查询
{
     
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
     
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++ ) add(i, a[i]);//构建树状数组

    while (m -- )
    {
     
        int k, x, y;
        scanf("%d%d%d", &k, &x, &y);
        if (k == 0) printf("%d\n", query(y) - query(x - 1));
        else add(x, y);
    }

    return 0;
}

如果出的题都像模板题那样就好了
世界并不是如此简单

实战题

数星星

天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。

如果一个星星的左下方（包含正左和正下）有 k 颗星星，就说这颗星星是 k 级的。

例如，上图中星星 5 是 3 级的（1,2,4 在它左下），星星 2,4 是 1 级的。

例图中有 1 个 0 级，2 个 1 级，1 个 2 级，1 个 3 级的星星。

给定星星的位置，输出各级星星的数目。

换句话说，给定 N 个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。

输入格式
第一行一个整数 N，表示星星的数目；

接下来 N 行给出每颗星星的坐标，坐标用两个整数 x,y 表示；

不会有星星重叠。星星按 y 坐标增序给出，y 坐标相同的按 x 坐标增序给出。

输出格式
N 行，每行一个整数，分别是 0 级，1 级，2 级，……，N−1 级的星星的数目。

数据范围
1≤N≤15000,
0≤x,y≤32000
输入样例：

5
1 1
5 1
7 1
3 3
5 5

输出样例：

1
2
1
1
0

题目分析：
若坐标为(x,y)则求坐标小于等于x，小于等于y的星星数量
看似是一个二维前缀和计算，可是仔细分析可知，按照每一层从左到右，层数从下向上给出星星作标，易知当给出当前坐标时，y>=之前的星星y坐标，所以只用看x坐标即可，看看比当前坐标的x小于等于的之前的星星x坐标数量即可求出当前坐标星星的等级,跟y值无关

代码：

#include 
#include 
#include 
#include 

using namespace std;

const int N = 32010;

int n;
int tr[N], level[N];

int lowbit(int x)
{
     
    return x & -x;
}

void add(int x)
{
     
    for (int i = x; i < N; i += lowbit(i)) tr[i] ++ ;
}

int sum(int x)
{
     
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
     
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ )
    {
     
        int x, y;
        scanf("%d%d", &x, &y);
        x ++ ;//树状数组下标从1开始
        level[sum(x)] ++ ;//确定当前星星的等级
        add(x);//将当前星星的放入树状数组
    }

    for (int i = 0; i < n; i ++ ) printf("%d\n", level[i]);

    return 0;
}

线段树

形如完全二叉树
线段树和树状数组的关系

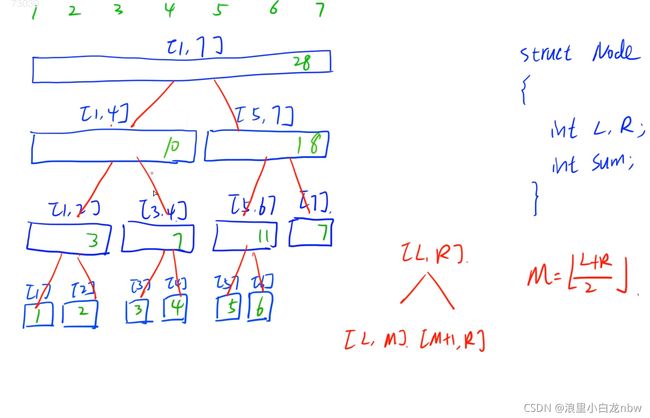
线段树图形描述

相关操作

• 单点修改
• 区间查询
• 区间最大值
• …

1.对于单点修改，会先递归的找到需要修改的叶节点，修改后进行回溯，边回溯边更新与此叶节点有关的数据
2. 对于区间查询也是递归进行，如果当前区间被完全包括在查询区间内则返回，否则继续递归查询与查询区间有关的区间
若查询区间2-5

对于节点x

• 父节点：x/2向下取整 （x>>1）
• 左节点: 2*x （x<<1）
• 右节点:2*x+1 （x<<1 | 1）

基本操作

1. pushup:用子节点信息更新当前节点信息
2. build在一段区间上初始化线段树
3. modify修改
4. query查询

注意事项：

• 线段树和堆是一种存储方式
• 线段树个数一般开4*n
• 下标从1开始

快速上手

模板题

动态求连续区间和
给定 n 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 [a,b] 的连续和。

输入格式
第一行包含两个整数 n 和 m，分别表示数的个数和操作次数。

第二行包含 n 个整数，表示完整数列。

接下来 m 行，每行包含三个整数 k,a,b （k=0，表示求子数列[a,b]的和；k=1，表示第 a 个数加 b）。

数列从 1 开始计数。

输出格式
输出若干行数字，表示 k=0 时，对应的子数列 [a,b] 的连续和。

数据范围
1≤n≤100000,
1≤m≤100000，
1≤a≤b≤n,
数据保证在任何时候，数列中所有元素之和均在 int 范围内。

输入样例：

10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8

输出样例：

11
30
35

代码如下：

#include 
#include 
#include 
#include 

using namespace std;

const int N = 100010;

int n, m;
int w[N];//相当于原始数组A
struct Node
{
     
    int l, r;
    int sum;
}tr[N * 4];//线段树的每一个节点

void pushup(int u)
{
     
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum; //根据子节点跟新当父节点
}

void build(int u, int l, int r)//u为当前节点编号
{
     
    if (l == r) tr[u] = {
     l, r, w[r]}; //如果当前节点是子节点就直接复制
    else
    {
     
        tr[u] = {
     l, r};//当前节点左右范围确定
        int mid = l + r >> 1;//我们以mid进行划分
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);//左右子树构建好之后，对当前节点更新
    }
}

int query(int u, int l, int r)
{
     	//如果查询区间完全包含当前节点则返回
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
    //否则寻找与查询区间相关的区间
    int mid = tr[u].l + tr[u].r >> 1;
    int sum = 0;
    if (l <= mid) sum = query(u << 1, l, r);
    if (r > mid) sum += query(u << 1 | 1, l, r);
    return sum;
}

void modify(int u, int x, int v)
{
     
    if (tr[u].l == tr[u].r) tr[u].sum += v;//修改子节点
    else//根据子节点更新父节点
    {
     
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

int main()
{
     
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
    build(1, 1, n);

    int k, a, b;
    while (m -- )
    {
     
        scanf("%d%d%d", &k, &a, &b);
        if (k == 0) printf("%d\n", query(1, a, b));
        else modify(1, a, b);
    }

    return 0;
}

快速上手实战题

数列区间最大值
输入一串数字，给你 M 个询问，每次询问就给你两个数字 X,Y，要求你说出 X 到 Y 这段区间内的最大数。

输入格式
第一行两个整数 N,M 表示数字的个数和要询问的次数；

接下来一行为 N 个数；

接下来 M 行，每行都有两个整数 X,Y。

输出格式
输出共 M 行，每行输出一个数。

数据范围
1≤N≤105,
1≤M≤106,
1≤X≤Y≤N,
数列中的数字均不超过231−1
输入样例：

10 2
3 2 4 5 6 8 1 2 9 7
1 4
3 8

输出样例：

5
8

代码

#include 
#include 
#include 
#include 
#include 

using namespace std;

const int N = 100010;

int n, m;
int w[N];
struct Node
{
     
    int l, r;
    int maxv;
}tr[N * 4];

void build(int u, int l, int r)
{
     
    if (l == r) tr[u] = {
     l, r, w[r]};
    else
    {
     
        tr[u] = {
     l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        tr[u].maxv = max(tr[u << 1].maxv, tr[u << 1 | 1].maxv);
    }
}

int query(int u, int l, int r)
{
     
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].maxv;
    int mid = tr[u].l + tr[u].r >> 1;
    int maxv = INT_MIN;
    if (l <= mid) maxv = query(u << 1, l, r);
    if (r > mid) maxv = max(maxv, query(u << 1 | 1, l, r));
    return maxv;
}

int main()
{
     
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);

    build(1, 1, n);

    int l, r;
    while (m -- )
    {
     
        scanf("%d%d", &l, &r);
        printf("%d\n", query(1, l, r));
    }

    return 0;
}

总结

本文主要以快速实战为主，原理可查阅相关资料，这里不再展开相关内容讲解