全国计算机等级考试二级Python(2021年9月)备考笔记 第三天
文章目录
- Python语言程序设计-嵩天老师(MOOC)听课笔记 第3周
-
- 知识点一
-
- 整数类型
- 浮点数类型
- 复数类型
- 数值运算操作符
- 数字类型的关系
- 数值运算函数
- 实例 天天向上的力量
-
- 问题3:工作日的力量
- 问题4:工作日的努力
- 知识点二
-
- 字符串
- 字符串切片高级用法
- 字符串的特殊字符
- 字符串操作符
- 字符串处理函数
- Unicode编码
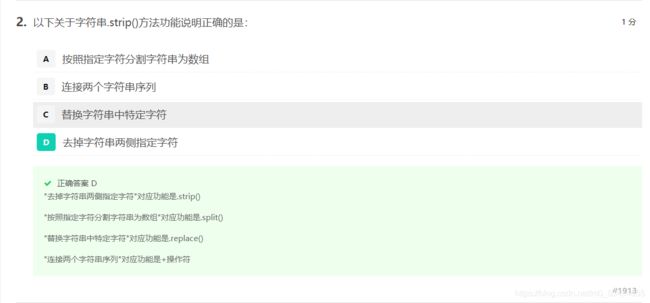
- 字符串处理方法
- 字符串类型的格式化
- format()方法的格式控制
- 知识点三
-
- time库的使用
- 时间格式化
- 程序计时
- 实例 文本进度条
-
- 需求分析
- 问题分析
- 简单的开始
- 单行动态刷新
- 完整效果
- 举一反三
- 课后练习题
-
- 实例一 天天向上的力量
- 实例二 文本进度条
- 实例三 三次方格式化
- 实例四 星号三角形
- 实例五 凯撒密码
- 第三周测验题目
-
- 单项选择题
- 程序设计题
-
- 第一题 平方根格式化
- 第二题 字符串分段组合
Python语言程序设计-嵩天老师(MOOC)听课笔记 第3周
知识点一
整数类型
- 与数学中整数的概念一致
- 可正可负,没有取值范围限制
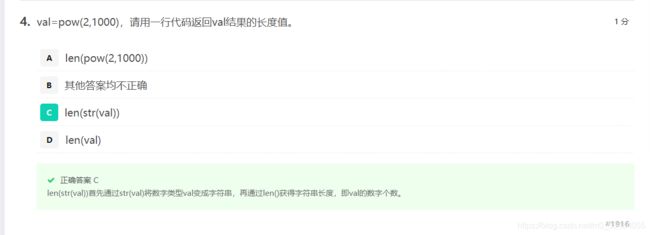
- p o w ( x , y ) pow(x,y) pow(x,y)函数:计算 x y , x^y, xy,想算多大算多大
>>> pow(2,100) 1267650600228229401496703205376
>>> pow(2,pow(2,15)) 1415461031044954789001553027744......
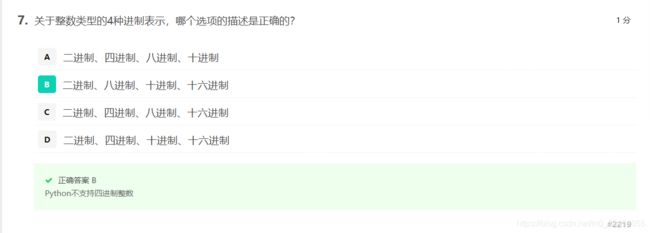
- 4种进制表示形式
- 十进制:1010,99,-217
- 二进制,以0b或0B开头:0b010,-0B101
- 八进制,以0o或0O开头:0o123,-0O456
- 十六进制,以0x或0X开头:0x9a,-0X89
浮点数类型
- 与数学中实数的概念一致
- 带有小数点及小数的数字
- 浮点数取值范围和小数精度都存在限制,但常规计算可忽略
- 取值范围数量级约 − 1 0 308 -10^{308} −10308至 1 0 308 10^{308} 10308,精度数量级 1 0 − 16 10^{-16} 10−16
- 浮点数间运算存在不确定尾数,不是bug
>>> 0.1+0.3
0.4
>>> 0.1+0.2
0.30000000000000004
>>>0.1+0.2==0.3
False
- 可使用 r o u n d round round函数解决该问题
>>>round(0.1+0.2,1)==0.3
True- r o u n d ( x , d ) round(x,d) round(x,d):对 x x x四舍五入, d d d是小数截取位数
浮点数间运算及比较 用 r o u n d ( ) round() round()函数辅助
不确定尾数一般发生在 1 0 − 16 10^{-16} 10−16左右, r o u n d ( ) round() round()十分有效
- 浮点数可以采用科学计数法表示
- 使用字母 e e e或 E E E作为幂的符号,以10为基数,格式如下:
< a > e < b > < a >e< b> <a>e<b> 表示 a ∗ 1 0 b a*10^b a∗10b
例如: 4.3 e − 3 值 为 0.0043 4.3e-3值为0.0043 4.3e−3值为0.0043 9.6 E 5 值 为 960000.0 9.6E5 值为960000.0 9.6E5值为960000.0
复数类型
- 与数学中复数的概念一致
如果 x 2 = − 1 x^2=-1 x2=−1,那么x的值是什么?
定义 j = ( − 1 ) j=\sqrt{(-1)} j=(−1),以此为基础,构建数学体系
a + b j a+bj a+bj被称为复数,其中, a a a是实部,b是虚部
- 复数实例
z = 1.23 e − 4 + 5.6 e + 89 j z=1.23e-4+5.6e+89j z=1.23e−4+5.6e+89j
实部是什么? z . r e a l z.real z.real获得实部
虚部是什么? z . i m a g z.imag z.imag获得虚部
数值运算操作符
- 操作符是完成运算的一种符号体系
| 操作符及使用 | 描述 |
|---|---|
| + x +x +x | x x x本身 |
| − y -y −y | y y y的负值 |
| x x x % y y y | 余数,模运算 10%3结果是1 |
| x ∗ ∗ y x**y x∗∗y | 幂运算, x x x的 y y y次幂, x y x^y xy;当 y y y是小数时,开方运算10**0.5结果是 10 \sqrt{10} 10 |
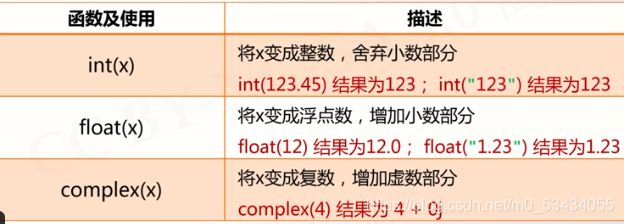
数字类型的关系
三种类型存在一种逐渐"扩展"或"变宽"的关系:
整数 → \rarr → 浮点数 → \rarr → 复数
例如:123+4.0=127.0 (整数+浮点数=浮点数)
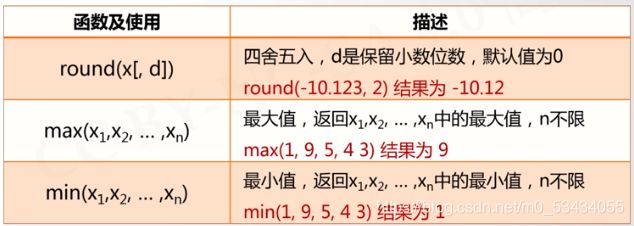
数值运算函数
- 一些以函数形式提供的数值运算功能
实例 天天向上的力量
问题3:工作日的力量
题目描述:
- 一年365天,一周5个工作日,每天进步1%
- 一年365天,一周2个休息日,每天退步1%
- 这种工作日的力量,如何呢?
代码如下:
dayup=1.0
dayfactor=0.01
for i in range(365): #采用循环模拟365天的过程
if i % 7 in [6,0]:
dayup=dayup*(1-dayfactor)
else:
dayup=dayup*(1+dayfactor)
print("工作日的力量:{:.2f}".format(dayup))
问题4:工作日的努力
题目描述:
- 工作日模式要努力到什么水平,才能与每天努力1%的效果一样?
- A君:一年365天,每天进步1%,不停歇
- B君:一年365天,每周工作5天休息2天,休息日下降1%,要多努力呢?
f o r . . . i n . . . ( 计 算 思 维 ) for...in...(计算思维) for...in...(计算思维) → \rightarrow → d e f . . . w h i l e . . . ( " 笨 方 法 " 试 错 ) def...while...("笨方法"试错) def...while...("笨方法"试错)
代码如下:
def dayUP(df): #def保留字用于定义函数,根据df参数计算工作日力量的函数,参数不同代码可共用
dayup=1
for i in range(365)
if i % 7 in [6,0]:
dayup=dayup*(1-0.01)
else:
dayup=dayup*(1+df)
return dayup
dayfactor=0.01
while dayUP(dayfactor)<37.78 #while保留字判断条件是否成立,条件成立时循环执行
daydactor+=0.001
print("工作日的努力参数是:{:.3f}".format(dayfactor))
#代码运行结果:工作日的努力参数是:0.019
知识点二
字符串
- 由0个或多个字符组成的有序字符序列
- 字符串由一对单引号或一对双引号表示
"请输入带有符号的温度值:"或者'C'- 字符串是字符的有序序列,可以对其中的字符进行索引
"请"是"请输入带有符号的温度值:"的第0个字符
- 字符串有2类共4种表示方法
- 由一对单引号或双引号表示,仅表示单行字符串
"请输入带有符号的温度值:"或者'C'- 由一对单三引号或三双引号表示,可表示多行字符串
'''Python
语言'''- 如果希望在字符串中包含双引号或单引号呢?
'这里有个双引号(")'或者"这里有个单引号(')"- 如果希望在字符串中既包括单引号又包含双引号
'''这里既有单引号(')又有双引号(")'''
字符串切片高级用法
- 使用[M:N:K]根据步长对字符串切片
- <字符串>[M:N],M缺失表示至开头,N缺失表示至结尾
"〇一二三四五六七八九十"[:3]结果是"〇一二"- <字符串>[M:N:K],根据步长K对字符串切片
"〇一二三四五六七八九十"[1:8:2]结果是"一三五七"
"〇一二三四五六七八九十"[::-1]结果是"十九八七六五四三二一〇"
字符串的特殊字符
- 转义符\
- 转义符表达特定字符的本意
"这里有个双引号(\")" 结果为 这里有个双引号(")- 转义符形成一些组合,表达一些不可打印的含义
"\b"回退 "\n"换行(光标移动到下行首) "\r"回车(光标移动到本行首)
字符串操作符
- 由0个或多个字符组成的有序字符序列
| 操作符及使用 | 描述 |
|---|---|
| x + y x+y x+y | 连接两个字符串 x 和 y x和y x和y |
| n ∗ x 或 x ∗ n n*x 或 x*n n∗x或x∗n | 复制 n n n次字符串 x x x |
| x x x i n in in s s s | 如果 x x x是 s s s的子串,返回 T r u e True True,否则返回 F a l s e False False |
- 获取星期字符串
代码一:
weekStr="星期一星期二星期三星期四星期五星期六星期日"
weekId=eval(input("请输入星期数字(1-7):"))
pos=(weekId-1)*3
print(weekStr[pos:pos+3])
代码二:
weekStr="一二三四五六日"
weekId=eval(input("请输入星期数字(1-7):"))
print("星期"+weekStr[weekId-1])
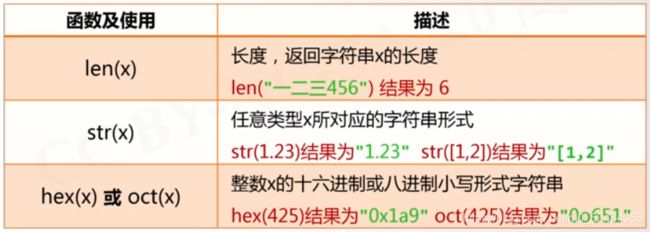
字符串处理函数
- 一些以函数形式提供的字符串处理功能
Unicode编码
- Python字符串的编码方式
- 统一字符编码,即覆盖几乎所有字符的编码方式
- 从0到1114111(0x10FFFF)空间,每个编码对应一个字符
- Python字符串中每个字符都是Unicode编码字符
- 一些有趣的例子
>>>"1+1=2"+chr(10004)
'1+1=2✔'
>>> "这个字符♉的Unicode值是:"+str(ord("♉"))
'这个字符♉的Unicode值是:9801'
>>> for i in range(12):
print(chr(9800+i),end="")
♈♉♊♋♌♍♎♏♐♑♒♓
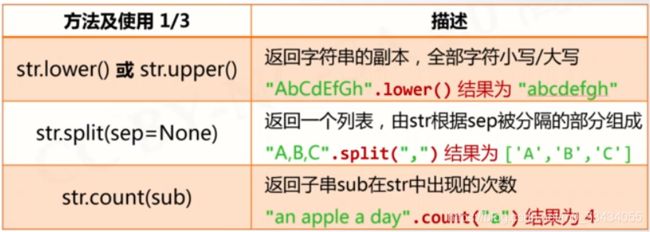
字符串处理方法
- "方法"在编程中是一个专有名词
- "方法"特指< a >.< b >()风格中的函数< b >()
- 方法本身也是函数,但与< a >有关,< a >.< b >()风格使用
- 字符串及变量也是< a >,存在一些方法
- 一些以方法形式提供的字符串处理功能
字符串类型的格式化
- 格式化是对字符串进行格式表达的方式
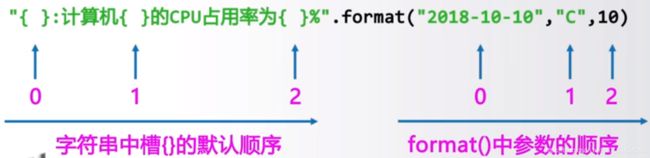
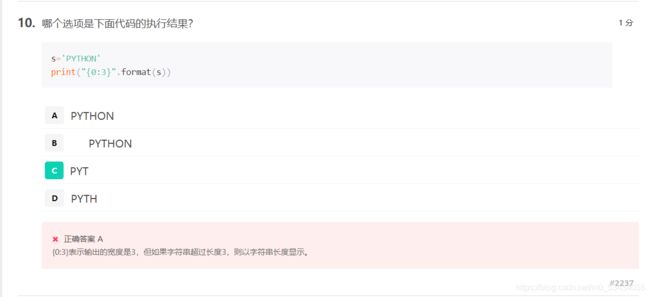
format()方法的格式控制
':','填充','对齐','宽度'示例:
>>> "{0:=^20}".format("PYTHON") # '='为填充符号,'^'表示居中,'20'表示字符串宽度
'=======PYTHON======='
>>> "{0:*>20}".format("BIT") # '*'为填充符号,'>'表示右对齐,'20'表示字符串宽度
'*****************BIT'
>>> "{:10}".format("BIT") #默认以' '(空格)填充、左对齐,'10'表示字符串宽度
'BIT '
',','.精度','类型'示例:
>>> "{0:,.2f}".format(12345.6789)
'12,345.68'
>>> "{0:b},{0:c},{0:d},{0:o},{0:x},{0:X}".format(425) #:b 二进制形式;:c 字符形式;:d 十进制表示形式;:0 八进制表示形式;:x 十六进制表示形式;:X 大写的十六进制表示形式
'110101001,Ʃ,425,651,1a9,1A9'
>>> "{0:e},{0:E},{0:f},{0:%}".format(3.14) #:e 表示以科学计数法e形式表示浮点数;:E 表示以科学计数法E形式表示浮点数;:f 表示以非科学计数法形式表示浮点数;:% 表示以百分数形式表示浮点数
'3.140000e+00,3.140000E+00,3.140000,314.000000%'
知识点三
time库的使用
- time库是Python中处理时间的标准库
- 计算机时间的表达
- 提供获取系统时间并格式化输出功能
- 提供系统级精确计时功能,用于程序性能分析
import time
time.()
- time库包含三类函数
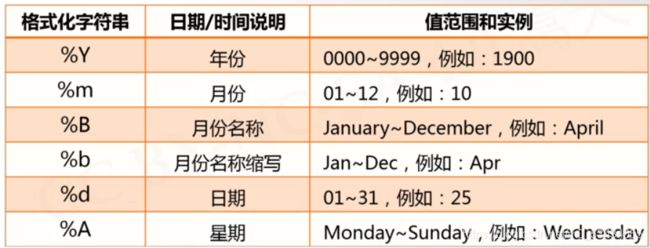
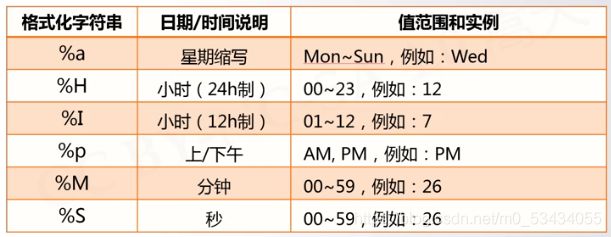
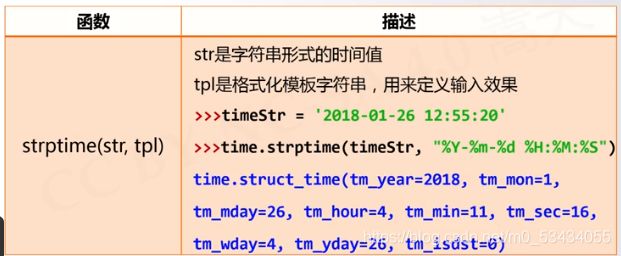
时间格式化
- 将时间以合理的方式展示出来
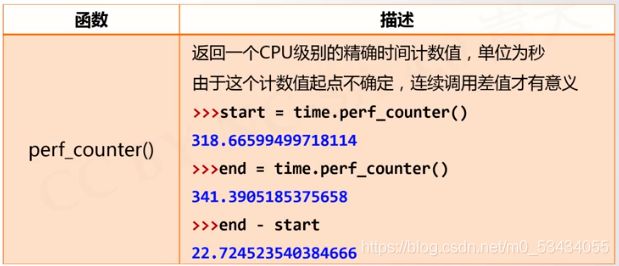
程序计时
- 程序计时应用广泛
实例 文本进度条
需求分析
- 文本进度条
- 采用字符串方式打印可以动态变化的文本进度条
- 进度条需要能在一行中逐渐变化
问题分析
- 如何获得文本进度条的变化时间
- 采用sleep()模拟一个持续的进度
- 似乎不那么难
简单的开始
import time
scale=10
print("------执行开始------")
for i in range(scale+1):
a='*'*i #'*'被复制i次后赋给a
b='.'*(scale-i) #'.'被复制(scale-i)次后赋给b
c=(i/scale)*100 #当前进度与scale的百分比
print("{:^3.0f}%[{}->{}]".format(c,a,b))
time.sleep(0.1)
print("------执行结束------")
'''输出结果:
------执行开始------
0 %[->..........]
10 %[*->.........]
20 %[**->........]
30 %[***->.......]
40 %[****->......]
50 %[*****->.....]
60 %[******->....]
70 %[*******->...]
80 %[********->..]
90 %[*********->.]
100%[**********->]
------执行结束------'''
单行动态刷新
- 刷新的关键是\r
- 刷新的本质是:用后打印的字符覆盖之前的字符
- 不能换行:print()需要被控制
- 要能回退:打印后光标退回到之前的位置\r
import time
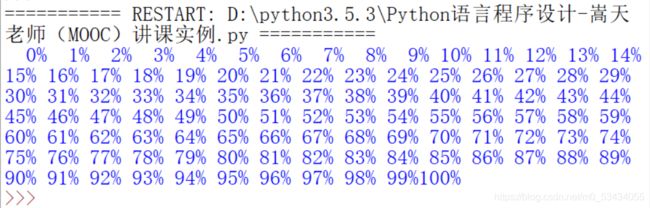
for i in range(101):
print("\r{:3}%".format(i),end="") #end="" 使print输出后不再换行;idle为开发环境,自动屏蔽\r功能,会产生图示效果,全部展示,并不表现为刷新效果,可通过双击.py文件,就可以正常运行程序
time.sleep(0.1)
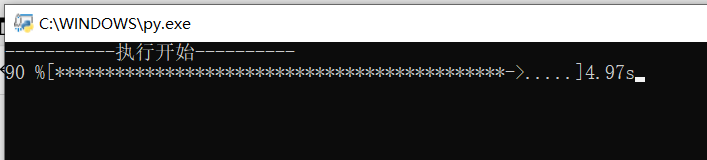
完整效果
import time
scale=50
print("执行开始".center(scale//2,"-"))
start=time.perf_counter()
for i in range(scale+1):
a='*'*i #'*'被复制i次后赋给a
b='.'*(scale-i) #'.'被复制(scale-i)次后赋给b
c=(i/scale)*100 #当前进度与scale的百分比
dur=time.perf_counter() - start
print("\r{:^3.0f}%[{}->{}]{:.2f}s".format(c,a,b,dur),end='')
time.sleep(0.1)
print("\n"+"执行结束".center(scale//2,'-'))
举一反三
- 计算问题扩展
- 文本进度条程序使用了perf_counter()计时
- 计时方法适合各类需要统计时间的计算问题
- 例如:比较不同算法时间、统计部分程序运行时间
- 进度条扩展
- 在任何运行时间需要较长的程序中增加进度条
- 在任何希望提高用户体验的应用中增加进度条
- 进度条是人机交互的纽带之一
课后练习题
实例一 天天向上的力量
题目描述:每周工作5天休息2天,计算工作日的努力参数是多少才能与每天努力1%一样?
- A君: 一年365天,每天进步1%,不停歇
- B君: 一年365天,每周工作5天休息2天,休息日下降1% ,要多努力呢?
题目要求:
(1) 一年365天,以第0天的能力值为基数,记为1.0;
(2) 当好好学习时,能力值相比前一天提高1%;当没有学习时,由于遗忘等原因能力值相比前一天下降1%;
输出示例:
工作日的努力参数是: 0.019
代码如下:
def dayUP(df):
dayup = 1
for i in range(365):
if i % 7 in [6,0]:
dayup = dayup*(1 - 0.01)
else:
dayup = dayup*(1 + df)
return dayup
dayfactor = 0.01
while dayUP(dayfactor) < 37.78:
dayfactor += 0.001
print("工作日的努力参数是: {:.3f}".format(dayfactor))
实例二 文本进度条
题目描述:采用字符串方式打印可以动态变化的文本进度条,进度条需要能在一行中逐渐变化
题目要求:
- (1) 采用sleep()模拟一个持续的进度,获得文本进度条的变化时间;
- (2) 通过print()函数实现单行动态刷新,在print()函数中更换参数end的默认值为’’,每次使用print()函数输出时不能换行;
- (3) 要能回退:打印后光标到之前的位置\r。
代码如下:
import time
scale = 50
print("执行开始".center(scale//2,'-'))
start = time.perf_counter()
for i in range(scale+1):
a = '*' * i
b = '.' * (scale - i)
c = (i/scale)*100
dur = time.perf_counter() - start
print("\r{:^3.0f}%[{}->{}]{:.2f}s".format(c,a,b,dur),end='')
time.sleep(0.1)
print("\n"+"执行结束".center(scale//2,'-'))
实例三 三次方格式化
题目描述:获得用户输入的一个数字,可能是整数或浮点数,a,计算a的三次方值,并打印输出。
输出结果采用宽度20个字符、居中输出、多余字符采用减号(-)填充。
如果结果超过20个字符,则以结果宽度为准。
输出示例:
--------1000--------
代码如下:
a = eval(input())
print("{:-^20}".format(pow(a, 3)))
实例四 星号三角形
题目描述:读入一个整数N,N是奇数,输出由星号字符组成的等边三角形
题目要求:第1行1个星号,第2行3个星号,第3行5个星号,依次类推,最后一行共N个星号
代码如下:
n = eval(input())
for i in range(1,n+1,2):
print("{0:^{1}}".format('*'*i, n))
实例五 凯撒密码
题目描述:恺撒密码是古罗马恺撒大帝用来对军事情报进行加解密的算法,它采用了替换方法对信息中的每一个英文字符循环替换为字母表序列中该字符后面的第三个字符,即,字母表的对应关系如下:
原文:A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
密文:D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
对于原文字符P,其密文字符C满足如下条件:C=(P+3) mod 26
上述是凯撒密码的加密方法,解密方法反之,即:P=(C-3) mod 26
假设用户可能使用的输入包含大小写字母a~ z,A~Z、空格和特殊符号,请编写一个程序,对输入字符串进行恺撒密码加密,直接输出结果,其中空格不用进行加密处理。使用input()获得输入。
输入示例
python is good
输出示例
sbwkrq lv jrrg
代码如下:
s = input()
t = ""
for c in s:
if 'a' <= c <= 'z':
t += chr( ord('a') + ((ord(c)-ord('a')) + 3 )%26 )
elif 'A' <= c <= 'Z':
t += chr( ord('A') + ((ord(c)-ord('A')) + 3 )%26 )
else:
t += c
print(t)
第三周测验题目
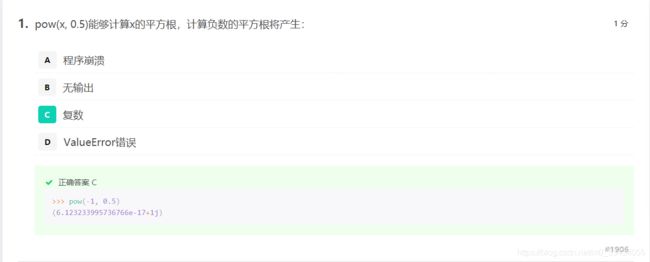
单项选择题
程序设计题
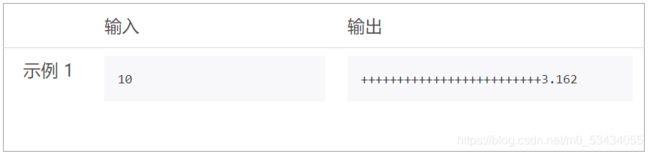
第一题 平方根格式化
题目描述:获得用户输入的一个整数a,计算a的平方根,保留小数点后3位,并打印输出。
输出结果采用宽度30个字符、右对齐输出、多余字符采用加号(+)填充。
如果结果超过30个字符,则以结果宽度为准。
输入输出示例:
代码如下:
a=input()
b=pow(eval(a),0.5)
print("{0:+>30.3f}".format(b))
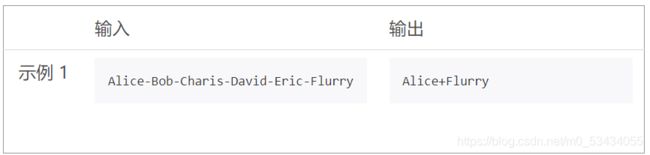
第二题 字符串分段组合
代码如下:
a=input()
b=a.split("-")
print(b[0]+"+"+b[-1])