机器学习之k-近邻算法(KNN)
机器学习之k-近邻算法(KNN)
- k-近邻算法的概念
- k-近邻算法流程及实现详解
-
- 算法概述
- 问题描述
- k-近邻算法
- 将文本记录转换为NumPy的解析程序
- 归一化特征值
- 分类器针对约会网站的测试代码
- 约会网站测试函数
k-近邻算法的概念

简单地说,k-近邻算法采用测量不同特征值之间的距离方法进行分类。
它的工作原理是:存在一个样本数
据集合,也称作训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一数据
与所属分类的对应关系。输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的
特征进行比较,然后算法提取样本集中特征最相似数据(最近邻)的分类标签。一般来说,我们
只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。
最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
优点:精度高、对异常值不敏感、无数据输入假定。
缺点:计算复杂度高、空间复杂度高。
适用数据范围:数值型和标称型。
让我们从一个简单的例子开始看起
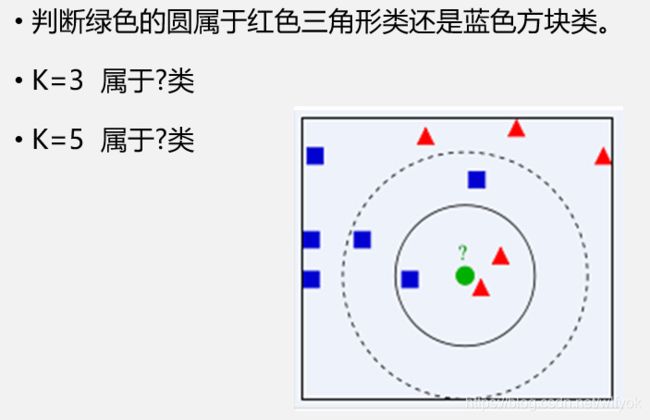
图中绿色的带判定的圆形到底是属于红色三角形还是蓝色方块呢?如果在第一个圆圈内(k=3),很明显可以看出,圆里三角形最近,因此我们将其判断为三角形;如果k=5,即在第二个圆圈内,和绿色圆形最近的蓝色方形大于红色三角形的个数,因此我们将圆形归类为蓝色的方形。可以看出,圆形的分类很大一部分取决于k的取值。

让我们继续看另一个例子:

我们是否可以根据上图所给出的数据来判断《?》的电影类型呢?
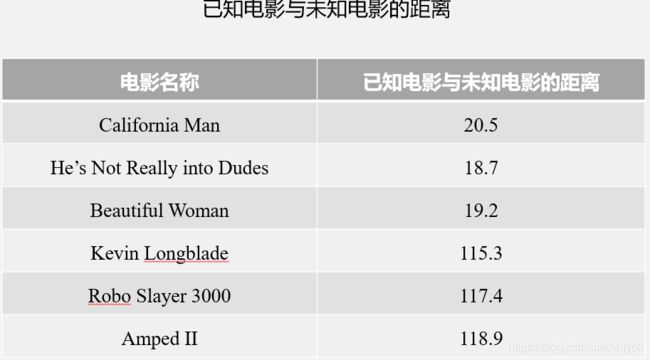
根据上面将圆形划分为方形或三角形的例子中,我们仿照距离的定义,可以将电影的类型进行分类。将未知电影与已知电影的距离进行比较,比较距离最终得出电影的类型。那么问题来了,这里的距离是一个什么概念呢?

在《数值分析》或《实变函数与泛函分析》中有对各种距离的定义,我们引出其中比较经典的集中距离。通常,我们使用的k-近邻算法中采用的欧氏距离。
k-近邻算法流程及实现详解
算法概述
在已经大致了解了k-近邻算法的概念和其工作原理之后,我们就开始进行算法的讲解和实现。首先,我们给出k-近邻算法的一般流程。
(1) 收集数据:可以使用任何方法。
(2) 准备数据:距离计算所需要的数值,最好是结构化的数据格式。
(3) 分析数据:可以使用任何方法。
(4) 训练算法:此步骤不适用于k-近邻算法。
(5) 测试算法:计算错误率。
(6) 使用算法:首先需要输入样本数据和结构化的输出结果,然后运行k-近邻算法判定输
入数据分别属于哪个分类,最后应用对计算出的分类执行后续的处理。

问题描述
我们使用算法来实现一个实例,依次来进行实战——使用 k-近邻算法改进约会网站的配对效果。
实例:我的朋友海伦一直使用在线约会网站寻找适合自己的约会对象。尽管约会网站会推荐不同的
人选,但她没有从中找到喜欢的人。经过一番总结,她发现曾交往过三种类型的人:
不喜欢的人
魅力一般的人
极具魅力的人
尽管发现了上述规律,但海伦依然无法将约会网站推荐的匹配对象归入恰当的分类。她觉得
可以在周一到周五约会那些魅力一般的人,而周末则更喜欢与那些极具魅力的人为伴。海伦希望
我们的分类软件可以更好地帮助她将匹配对象划分到确切的分类中。此外海伦还收集了一些约会
网站未曾记录的数据信息,她认为这些数据更有助于匹配对象的归类

问题的数据集(在blog上不方便载入)在评论区获取,源码已经在下面给出
海伦收集约会数据已经有了一段时间,她把这些数据存放在文本文件datingTestSet.txt中,每
个样本数据占据一行,总共有1000行。海伦的样本主要包含以下3种特征:
每年获得的飞行常客里程数
玩视频游戏所耗时间百分比
每周消费的冰淇淋公升数
在将上述特征数据输入到分类器之前,必须将待处理数据的格式改变为分类器可以接受的格
式。在kNN.py中创建名为file2matrix的函数,以此来处理输入格式问题。该函数的输入为文
件名字符串,输出为训练样本矩阵和类标签向量。
接下来是算法实现函数的解析,解释都附在代码的注释里了。
k-近邻算法
def classify0(inX, dataSet, labels, k):
dataSetSize = dataSet.shape[0] # 获得属性格式
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet # 把inX按照(dataSetSize,1)的格式构造成矩阵
sqDiffMat = diffMat**2 # 元素的平方
sqDistances = sqDiffMat.sum(axis=1) # 按行求和
distances = sqDistances**0.5
sortedDistIndicies = distances.argsort() # 返回排序成功后元素从大到小的排列的下标
classCount = {
} # 字典
for i in range(k): # 选择最先的k个点,这里的k是我们输出的参数
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) # 排序
return sortedClassCount[0][0]
将文本记录转换为NumPy的解析程序
def file2matrix(filename):
love_dictionary = {
'largeDoses':3, 'smallDoses':2, 'didntLike':1}
fr = open(filename)
arrayOLines = fr.readlines()
numberOfLines = len(arrayOLines) #get the number of lines in the file
returnMat = np.zeros((numberOfLines, 3)) #prepare matrix to return 最后一列是标签,所以没有取
classLabelVector = [] #prepare labels return
index = 0
for line in arrayOLines:
line = line.strip() # 去掉开头和结尾的空格
listFromLine = line.split('\t') # 按'\t'分割数据
returnMat[index, :] = listFromLine[0:3]
if(listFromLine[-1].isdigit()):
classLabelVector.append(int(listFromLine[-1]))
else:
classLabelVector.append(love_dictionary.get(listFromLine[-1]))
index += 1
return returnMat, classLabelVector
归一化特征值
def autoNorm(dataSet):
minVals = dataSet.min(0) # 按列获得最小值
maxVals = dataSet.max(0) # 按行获得最大值
ranges = maxVals - minVals
normDataSet = np.zeros(np.shape(dataSet))
m = dataSet.shape[0] # 获得记录数
normDataSet = dataSet - np.tile(minVals, (m, 1))
normDataSet = normDataSet/np.tile(ranges, (m, 1)) #element wise divide
return normDataSet, ranges, minVals
分类器针对约会网站的测试代码
def datingClassTest():
hoRatio = 0.50 #hold out 10% 将10%作为测试集,90%作为训练集
datingDataMat, datingLabels = file2matrix('datingTestSet2.txt') #load data setfrom file
normMat, ranges, minVals = autoNorm(datingDataMat)
m = normMat.shape[0] # 样本个数
numTestVecs = int(m*hoRatio) # 测试样本的个数
errorCount = 0.0 # 初始误差
for i in range(numTestVecs):
classifierResult = classify0(normMat[i, :], normMat[numTestVecs:m, :], datingLabels[numTestVecs:m], 3)
print("the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]))
if (classifierResult != datingLabels[i]): errorCount += 1.0
print("the total error rate is: %f" % (errorCount / float(numTestVecs))) # 计算并输出误差率
print(errorCount)
机器学习算法一个很
重要的工作就是评估算法的正确率,通常我们只提供已有数据的90%作为训练样本来训练分类
器,而使用其余的10%数据去测试分类器,检测分类器的正确率。本书后续章节还会介绍一些高
级方法完成同样的任务,这里我们还是采用最原始的做法。

分类器处理约会数据集的错误率是2.4%,这是一个相当不错的结果。我们可以改变函数
datingClassTest内变量hoRatio和变量k的值,检测错误率是否随着变量值的变化而增加。依
赖于分类算法、数据集和程序设置,分类器的输出结果可能有很大的不同。
这个例子表明我们可以正确地预测分类,错误率仅仅是2.4%。海伦完全可以输入未知对象的
属性信息,由分类软件来帮助她判定某一对象的可交往程度:讨厌、一般喜欢、非常喜欢。
说明算法的准确度是很高的,下面我们就使用实例来进行对k-近邻算法的测试:
约会网站测试函数
def classifyPerson():
resultList = ['not at all', 'in small doses', 'in large doses']
percentTats = float(input(\
"percentage of time spent playing video games?"))
ffMiles = float(input("frequent flier miles earned per year?"))
iceCream = float(input("liters of ice cream consumed per year?"))
datingDataMat, datingLabels = file2matrix('datingTestSet2.txt')
normMat, ranges, minVals = autoNorm(datingDataMat)
inArr = np.array([ffMiles, percentTats, iceCream, ])
classifierResult = classify0((inArr - \
minVals)/ranges, normMat, datingLabels, 3)
print("You will probably like this person: %s" % resultList[classifierResult - 1])
