性感荷官在线发牌，真的靠谱吗？

前言

性感荷官在线发牌…真的不靠谱！

你是否有同样的经历，被眼前的利益蒙蔽了双眼，到头来却是一场空？那些年我们遇到过的网赌套路，跟着kimol君一起来看看叭。

一、十赌九骗

所谓赌博，严格来说，应该是建立在双方公平的基础上进行的博弈。然而，坊间流传着这么一句话：网络上的赌博十赌九骗。既然为骗，岂有不输之理？
而其诈骗流程，大抵如下：

很显然，无论过程再怎么曲折复杂，如果上了网骗的当，最终的结局都将是被骗，猝！
因此，还是珍爱健康，远离网赌为妙~

二、不公平的赔率

抛开网骗的情况不说，在各种所谓的“正规平台”，我们会发现这样一个规则：下注1元，中了返1.98元。这也意味着我们的赔率仅为0.92，这于1相差了仅0.02。而您可别小看了这0.02，就是它便可能让你输得精光。接下来，我们通过python做一个简单的模拟：

# -*- coding: utf-8 -*-
"""
Created on Sun Nov 22 10:07:39 2020

@author: kimol_love
"""
import random
import matplotlib.pyplot as plt

# 定义本金、赔率等参数
benjin = 1000   # 本金
peilv = 0.98    # 赔率
n = 10          # 每次下注金额
N = 1000000     # 模拟次数
money = benjin  # 余额（赔率为0.98）
money_n = benjin     # 余额（赔率为1.00）
money_list = [money] # 余额列表
money_list_n = [money_n] # 余额列表

# 模拟下注
for i in range(N):
    if random.random() < 0.5:
        money += n*peilv
        money_n += n*1.0
    else:
        money -= n*1.0
        money_n -= n*1.0
    if money < n or money_n < n: # 如果余额小于下注金额
        print('%d次破产!'%i)
        break
    money_list.append(money)
    money_list_n.append(money_n)

# 结果可视化
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.title('不公平的赔率')
plt.xlabel('下注次数')
plt.ylabel('余额')
plt.plot(money_list,label='赔率:0.98')
plt.plot(money_list_n,label='赔率:1.00')
plt.legend()

我们通过模拟来看赔率为1.00和0.98时余额的变化，结果如下：

显然，不同的赔率决定了不同的解决，一个“天上”，一个地上~
特别说明：这里假设输赢的概率是相等的，而如果输赢概率不一样的话，结果就更加可想而知了。

因此，简单地讲，从概率上你就输了。

三、所谓的倍投

想必大家应该听过倍投策略，也就是说：赢了就继续投，输了就按照当前下注额翻倍投，一直到赢了为止，这样一来之前所有输的都会回本，并且还会赢。当第n次赢时，其公式为：
$$\begin{gathered} lose=1+2+2^2+...+2^{n-1}=2^n-1 \\ win=2^n \\ profit=win-lose=1 \end{gathered}$$
显然，理论上讲这是稳赚的买卖，然而事实真的如此吗？

首先，在许多平台都限制了最高的倍率，因此你不可能无限倍投。
其次，想要一直倍投下去的前提是拥有足够的资本，而资本越多你能够抵御的风险就越高（即倍投的次数就越多），这便是所谓的资本抵御风险。我们有如下模拟：

# -*- coding: utf-8 -*-
"""
Created on Sun Nov 22 10:07:39 2020

@author: kimol_love
"""
import random
import matplotlib.pyplot as plt

benjins = range(1,11)
jieguo = [] # 本金数和对应的平均破产次数
# 模拟本金
for benjin in benjins:
    pochan = []
    ## 模拟轮数
    for k in range(1000000):
        ### 定义参数
        n = 1           # 每次下注金额
        N = 1000000     # 模拟次数
        money = benjin  # 余额
        money_list = [money] # 余额列表
        
        ### 模拟下注
        for i in range(N):
            if random.random() < 0.5:
                money += n
                n = 1 # 恢复正常
            else:
                money -= n
                n *= 2 # 倍投
            if money < n: # 如果余额小于下注金额
                pochan.append(i)
                break
            money_list.append(money)
    
    # 结果可视化
    jieguo.append(sum(pochan)/len(pochan))
    print('本金为：%d；平均破产次数：%d'%(benjin,sum(pochan)/len(pochan)))

# 可视化
plt.title('资产与风险的关系')
plt.xlabel('本金')
plt.ylabel('平均破产次数')
plt.plot(benjins,jieguo)

结果如下：

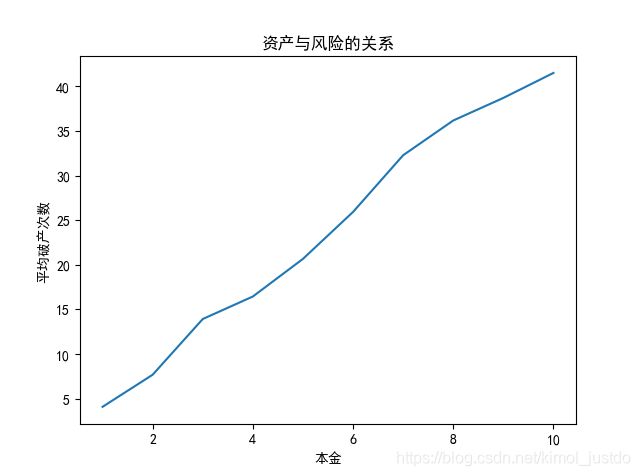
可以看出，在倍投的情况下，本金越多，破产所需要的次数也就越多。可以预想到：当你拥有无限的本金时，你将不会破产，稳赚不赔！
可是，你都有那么多钱了，还去赌博干嘛呢？

所以，倍投只是意味着理论上的不败，实际却…

四、赌徒谬论

在“赌界”，有许多人也许会这么认为：当骰子的点数连续出现了8、9次乃至更多次的大，那么，下一次出现得就很有可能是小，而这就是所谓的赌徒谬论。

受过九年义务的教育的我们，想必应该知道每次事件的出现是相互独立的，并不会受到先验结果的影响，而所谓的概率也仅适用于大数情况。
然而，即便道理如此简单，即便我们深知于心，那又如何？

当输时，有人总觉得“概率是均等的，再坚持坚持，没准马上便可翻盘！” 而结局，有可能便是千金散尽…（很显然，此时他是信奉赌徒谬论的）

当赢时，有人又觉得“运气大好，要乘胜追击，迎娶白富美便看今朝！”而解决，也许便是清洁溜溜…（很显然，此时赌徒谬论早已被他抛之脑后）

且不论这个谬论的正确与否，他们的做法就很矛盾。所以，问题来了：“赌徒们究竟是信还是不信赌徒谬论呢？” 我想只有贪欲能够回答这个问题叭~ 在贪婪面前，一切的理论、一切的技巧终究还是显得那么微不足道。

于是乎，我以为只有真正地修其心，养其性才是真正战胜赌的诀窍！

写在最后

以上仅代表kimol君个人的一些观点，如有不足还望大大们批评指正。另，实验模拟部分仍存在一些不严谨的地方，还望海涵~

愿各位小伙伴都能在这纷纷扰扰的世间坚守自己的那份光明，别被晦暗遮蔽了双眼，保护好自己的口袋，远离网赌！
最后，感谢各位大大的耐心阅读，咋们下次再会~

创作不易，大侠请留步… 动起可爱的双手，来个赞再走呗 (๑◕ܫ￩๑)