对SNAP图数据进行度分布统计
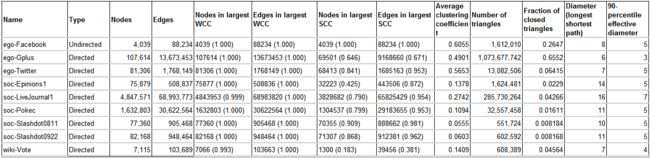
统计度分布的数据集
| Name | Type | Nodes | Edges | Description |
|---|---|---|---|---|
| ego-Facebook | Undirected | 4,039 | 88,234 | Social circles from Facebook (anonymized) |
| ego-Gplus | Directed | 107,614 | 13,673,453 | Social circles from Google+ |
| ego-Twitter | Directed | 81,306 | 1,768,149 | Social circles from Twitter |
| soc-Epinions1 | Directed | 75,879 | 508,837 | Who-trusts-whom network of Epinions.com |
| soc-LiveJournal1 | Directed | 4,847,571 | 68,993,773 | LiveJournal online social network |
| soc-Pokec | Directed | 1,632,803 | 30,622,564 | Pokec online social network |
| soc-Slashdot0811 | Directed | 77,360 | 905,468 | Slashdot social network from November 2008 |
| soc-Slashdot0922 | Directed | 82,168 | 948,464 | Slashdot social network from February 2009 |
| wiki-Vote | Directed | 7,115 | 103,689 | Wikipedia who-votes-on-whom network |
数据格式
数据集格式大多为A->B格式,部分数据集的数据注释:
wiki-Vote
# Directed graph (each unordered pair of nodes is saved once): Wiki-Vote.txt
# 有向图,每个节点的无序对只存在一次,即无重复
# Wikipedia voting on promotion to administratorship (till January 2008). Directed edge A->B means user A voted on B becoming Wikipedia administrator.
# 维基百科投票晋升到管理人的职位(直到2008年1月)。定向边缘A-B意味着用户A给用户B投票
# Nodes: 7115 Edges: 103689
# FromNodeId ToNodeId
30 1412
30 3352
...
soc-xx,eg:soc-Epinions1
# Directed graph (each unordered pair of nodes is saved once): soc-Epinions1.txt
# 有向图,每个节点的无序对只存在一次,即无重复
# Directed Epinions social network
# Nodes: 75879 Edges: 508837
# FromNodeId ToNodeId
0 4
0 5
...
ogo-xxx
数据文件较复杂,一般分为xxx,xxx-combined,readme三个文件;
xxx文件一般格式很复杂,具体意义待研究,这里体现网络的使用的是xxx-combined文件,
xxx-combind数据格式即A->B格式
数据集统计
相关的数据集统计都在SNAP对应的数据集页面有详细显示
节点度分布的计算
从小规模数据集ego-Facebook和wiki-Vote开始计算
A->B
A->C
A->D
B->D
B->A
ind(A)=1,outd(A)=3, d(A)=4
ind(B)=1,outd(B)=2, d(B)=3
ind(C)=1,outd(C)=0, d(C)=1
ind(D)=2,outd(D)=0, d(D)=2第一阶段:统计全部节点的度
构造思想
**map阶段:**
A->B拆分成'A-'+'-B',转换为KeyValuePair:和<-B,1>
即结果为:,<-B,1>,,<-C,1>,,<-D,1>,,<-D,1>,,<-A,1>
**reduce阶段:**
规约为,<-B,1>... 任务流程
- 启动集群(三虚拟机),start-all.sh开启hadoop(hdfs)
- 将源数据加载到hdfs
- 使用IDEA进行远程作业(mapreduce)提交
- 返回结果
实际操作:1.上传数据导hdfs
[hadoop@hadoop01 DATA0001]$ ls
facebook_combined.txt Slashdot0811.txt soc-Epinions1.txt soc-pokec-relationships.txt Wiki-Vote.txt gplus_combined.txt Slashdot0902.txt soc-LiveJournal1.txt twitter_combined.txt
[hadoop@hadoop01 ~]$ hadoop fs -mkdir /TVCG/SNAP
[hadoop@hadoop01 ~]$ hadoop fs -put DATA0001 /TVCG/SNAP/
#此过程可能会比较慢,会卡几分钟的时间(副本复制,分块等等)
上述意义是:该文件(400多M)被划分成了四个block,400/3=3.x 应该是4个block,正确无误
另外,当前块的所在节点为hadoop01,02,04,即此处是容错的三副本,这里可以优化一下,虚拟机小集群其实可以改为1,即取消副本,减少存储开销。
# 修改hdfs-site.xml的配置项,修改完需要重启hdfs!
dfs.replication
1
修改完后发现所在节点只剩下hadoop01了,因为关闭了三副本策略,所以四个节点只有hadoop01存有数据,同时作为namenode的01节点负担会很重,而且计算时会有网络传输开销,但是:
由于是虚拟机集群,存储是很宝贵的,网络传输开销显得不重要,所以这样没毛病(节省两倍空间)。
实际操作:2.构建mapreduce
先前的思路在实施起来有一定的复杂性,那么如果需求是计算节点的度,而且不分出度入度,那么可以简化成WordCount问题!
A->B
A->C
A->D
B->D
B->A
d(A)=4, d(B)=3, d(C)=1, d(D)=2第二阶段:对上述度数结果进行计数
构造思想
mapreduce结果:
A 4
B 3
C 2
D 2
度分布为:零次度1、两次度2、一次度3、一次度4实际操作
- 将mapred结果的key丢弃,只留下value,即度数
- 对度数进行统计计数
- 本步骤结果为
操作结果
mapreduce结果中的values再统计的结果:
<4,1>
<3,1>
<2,2>
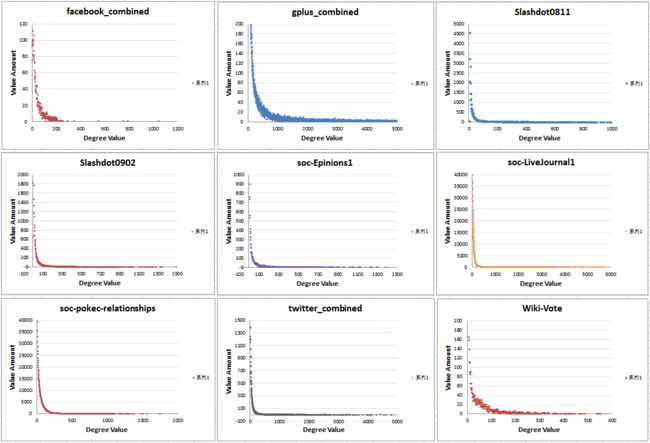
将上述结果画图即整个图的度分布为了验证度分布符合幂律的特点,可以分别将XY轴取ln底,那么图像会呈现一条斜率为负的倾斜直线,此斜率的大小正是(Y=cX^(-r))中的幂r的大小,由上面的叙述可知,可以通过对数底坐标轴的呈现图像是否为一条直线来判断度分布是不是符合幂律分布的特性。下面三组是上述九个数据集中度分布十分符合幂律分布的图像。
另外,由于数据及场景的特殊性,度分布并不一定完全符合幂律分布,或者说不可能完全符合,只是接近幂律的程度有大有小,下面三组就是九中数据集中符合幂律分布程度较差的图像。
度分布的统计学特性
(以下转自网络)
泊松分布和幂律分布
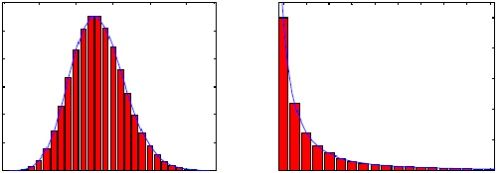
自然界与社会生活中,许多科学家感兴趣的事件往往都有一个典型的规模,个体的尺度在这一特征尺度附近变化很小。比如说人的身高,中国成年男子的身高绝大多数都在平均值1.70米左右,当然地域不同,这一数值会有一定的变化,但无论怎样,我们从未在大街上见过身高低于10厘米的“小矮人”,或高于10米的“巨人”。如果我们以身高为横坐标,以取得此身高的人数或概率为纵坐标,可绘出一条钟形分布曲线,这种曲线两边衰减地极快;类似这样以一个平均值就能表征出整个群体特性的分布,我们称之为泊松分布。
对于另一些分布,像国家GDP或个人收入的分布,情况就大不一样了,个体的尺度可以在很宽的范围内变化,这种波动往往可以跨越多个数量级。幂律分布的示意图如图1右图所示,其通式可写成y=cx^(−r),其中x,y是正的随机变量,c,r均为大于零的常数。这种分布(幂律分布)的共性是绝大多数事件的规模很小,而只有少数事件的规模相当大。对上式两边取对数,可知lny与lnx满足线性关系lny=lnc-rlnx,也即在双对数坐标下,幂律分布表现为一条斜率为幂指数的负数的直线,这一线性关系是判断给定的实例中随机变量是否满足幂律的依据。泊松分布(左)与“长尾”/幂律分布(右)。
从统计物理学来看,网络是一个包含了大量个体及个体之间相互作用的系统。近年来在对复杂网络的研究过程中,科学家们亦发现了众多的幂律分布,虽然这些网络在结构及功能上是如此的千变万化,相差迥异。复杂网络中 节点的度值k相对于 它的概率P(k)满足幂律关系,且幂指数多在大于2小于3的范围内;这一现象是如此的普遍,如此地令人惊叹不已,以至于人们给具有这种性质的网络起了一个特别的名字—— 无标度网络。这里的无标度是指网络 缺乏一个特征度值(或平均度值),即节点度值的波动范围相当大。
在过去的40多年里,科学家们一直想当然地认为现实中的网络都是随机的,随机图论就是专门为了研究随机网络而发展起来的一门数学学科,但无标度特性的发现打破了这种构想。随机网络的度分布是泊松分布,度值比平均值高许多或低许多的节点,都十分罕见,是一种高度 “民主”的网络,而无标度网络的度分布则是幂律分布,节点度值相差悬殊,往往可以跨越几个数量级,是一种极端 “专制”的网络,二者之间有本质的区别。这两种网络的一个形象化的比较如图所示。具有相同节点数和边数的随机网络(左)和无标度网络(右)。
度分布满足幂律的无标度网络还有一个奇特的性质—— “小世界”特性,虽然WWW中的页面数已超过80亿,但平均来说,在WWW上只需点击19次超链接,就可从一个网页到达任一其它页面。“小世界”现象在社会学上也称为 “六度分离”,它来源于1967年,美国哈佛大学的社会心理学家Milgram的一个实验,这个实验证实,世界上任何两个人,不论他(她)是中国的藏民,非洲的难民,还是美国的政界高层,好莱坞的明星,甚至北极的爱斯基摩人,美洲的土著印第安人,都可通过熟人找熟人的方式建立联系,而两者之间的平均最少“中介”数是6,如此看来,整个地球确实是一个小小的世界。
幂律分布于的判定
Zipf定律与Pareto定律都是简单的幂函数,我们称之为幂律分布;还有其它形式的幂律分布,像名次——规模分布、规模——概率分布,这四种形式在数学上是等价的,幂律分布的示意图如图1右图所示,其通式可写成y=c*x^(-r),其中x,y是正的随机变量,c,r均为大于零的常数。这种分布的共性是绝大多数事件的规模很小,而只有少数事件的规模相当大。对上式两边取对数,可知lny与lnx满足线性关系,也即在双对数坐标下,幂律分布表现为一条斜率为幂指数的负数的直线,这一线性关系是判断给定的实例中随机变量是否满足幂律的依据。判断两个随机变量是否满足线性关系,可以求解两者之间的相关系数;利用一元线性回归模型和最小二乘法可得lny对lnx的经验回归直线方程,从而得到y与x之间的幂律关系式。下图显示的是一般幂律分布(上一节第一幅图中的右图)在双对数坐标下的图形,由于某些因素的影响,下图前半部分的线性特性并不是很强,而在后半部分(对应于原图的尾部),则近乎为一直线,其斜率的负数就是幂指数。
幂律分布的形成机制
Barabási与Albert针对复杂网络中普遍存在的幂律分布现象,提出了网络动态演化的BA模型,他们解释,成长性和优先连接性是无标度网络度分布呈现幂律的两个最根本的原因。所谓成长性是指网络节点数的增加,像Internet中自治系统或路由器的添加,以及WWW中网站或网页的增加等,优先连接性是指新加入的节点总是优先选择与度值较高的节点相连,比如,新网站总是优先选择人们经常访问的网站作为超链接。随着时间的演进,网络会逐渐呈现出一种“富者愈富,贫者愈贫”的现象。社会学家所说的“马太效应”,《新约》圣经所说的“凡有的,还要加给他,叫他有余”,同优先连接也有某种相通之处。
“优先连接”并不适用于所有出现幂律分布的情况,即便是对于某些无标度网络,用它解释幂律的成因也显得很不合理(其他略)。
幂律分布的动力学影响
幂律特性的度分布对无标度网络的动力学性质有着极其深刻的影响。以疾病或病毒在网络中的传播这一物理过程为例,以前的基于规则网络及随机网络的研究表明,疾病的传染强度存在一个阈值,只有传染强度大于这个阈值时,疾病才能在网络中长期存在,否则感染人数会呈指数衰减。但对无标度网络上传染病模型的研究结果表明,不存在类似的阈值,只要传染病发生,就将长时间存在下去,这一特性表明,要想在Internet这样的无标度网络上彻底消灭病毒,即使是已知的病毒,也是不可能的。//区别规则网络、小世界网络、随机网络和无标度网络
另外,度分布的幂律特性对网络的容错性和抗攻击能力也有很大的影响,对网络的攻击分为随机攻击和选择性攻击两种类型,分别称为网络的容错能力与抗攻击能力。研究表明,无标度网络具有很强的容错性,但是对基于节点度值的选择性攻击抗攻击能力相当差。比如对万维网或因特网中集散节点的攻击,有可能造成整个网络的瘫痪,对于某些微生物来说,它们体内度值很高的蛋白质通常掌握着细胞的生死。度分布满足泊松分布的随机网络,其容错性和抗攻击能力则是基本相当的。可见,网络的结构稳定性是与网络的度分布特性紧密联系在一起的。
留下您对该文章的评价