学习笔记:数据结构(C语言版)线性表顺序结构
第二章 线性表
2.1 线性表的基本概念
线性结构是一种最简单且最常用的数据结构。
线性结构的基本特点是节点之间满足线性关系。
1.存在唯一的一个“第一元素”;
2.存在唯一的一个**“最后元素”** ;
3.除最后元素之外,均有唯一的后继;
4.除第一个元素之外,均有唯一的前驱。
动态数组,链表,栈,队列都属于线性结构。其共同之处,是节点中有且只有一个开始节点和终端节点。按照这种关系,可以把它们的所有节点排列成一个线性序列。(他们分别属于几种不同的抽象数据类型实现)。
线性表是零个或者多个数据元素的有限数列,
数据结构之间是有顺序的,数据元素个数是有限的,数据元素的类型必须相同。
线性表的实现
- 1. 顺序存储结构
- 2. 链式存储结构
2.2 线性表顺序存储(动态数组)的设计与实现
基本操作:
1. 线性表的定义
#define LTST_INIT_SIZE 100 //线性表存储空间的初始分配量
#define LISTINCREMENT 10 //线性表存储空间的分配增量
typedef struct
{
int *elem; // 存储空间的基址(注意:数组是一块连续的内存空间)
int length; //当前长度
int listsize; //当前分配的存储容量
} SqList;
//对typedef的理解: typedef 是C语言关键字,可以使用它来为数据类型取一个新的名字。
typedef unsigned int u32;
typedef struct _PERSON{
char name[64];
int age;
}Person;
void test(){
u32 val; //相当于 unsigned int val;
Person person; //相当于 struct PERSON person;
}
注意:(来源于菜鸟教程)
#define 是 C 指令,用于为各种数据类型定义别名,与 typedef 类似,但是它们有以下几点不同:
- typedef 仅限于为类型定义符号名称,#define 不仅可以为类型定义别名,也能为数值定义别名,比如您可以定义 1 为 ONE。
- typedef 是由编译器执行解释的,#define 语句是由预编译器进行处理的。
2. 线性表的初始化
//初始化
//C 库函数 void *malloc(size_t size) 分配所需的内存空间,并返回一个指向它的指针
//参数:size -- 内存块的大小,以字节为单位。
//返回值:该函数返回一个指针(void*) ,指向已分配大小的内存。如果请求失败,则返回 NULL
//在 C 语言中,sizeof() 是一个判断数据类型或者表达式长度的运算符,以字节为单位。
Status InitList_Sq(SqList &L)
{
//构造一个空的线性表
L.elem = (int*)malloc(LTST_INIT_SIZE*sizeof(int));
if (!L.elem) //判断空间是否分配成功 相当于 if(L.elem==NULL) NULL在C语言宏定义为 0/(void*)0
exit(OVERFLOW);
L.length = 0;
L.listsize = LTST_INIT_SIZE; //当前分配的存储容量 = 线性表存储空间的初始分配量
return OK;
}
结构销毁操作
3. 线性表的销毁
void DestroyList_Sq(SqList &L){
if (L.elem){ //相当于if(L.elem != NULL)
delete [] L.elem;
L.length = 0;
L.elem = NULL;
}
}
//拓展知识:
//C++释放堆区数组时:delete [] 数组名
person* pArray = new person[10];
delete [] pArray;
//如果不加[],则只释放第一个。
4. 线性表的清空
void ClearList(SqList &L){
L.length = 0;
printf("顺序表清空成功");
}
//拓展知识:
//C++引用:引用变量是一个别名,也就是说,它是某个已存在变量的另一个名字。一旦把引用初始化为某个变量,就可以使用该引用名称或变量名称来指向变量。
5. 判断线性表是否为空
//判断顺序表是否为空表
//在C89 (ANSI C)标准中没有定义与布尔类型相关的内容
//但在C99标准中新定义了一个新的关键字_Bool ,以及新增了一个头文件 规范了布尔类型的操作,方便程序员进行调用!
//但有些编译器中不支持C99类型
bool IsEmpty(SqList L){
if(L.length==0)
return true;
else
return false;
}
6. 返回数据元素的个数
typedef int Status;
//求顺序表的长度
Status GetLength(SqList L){
return L.length;
}
7. 给线性表元素赋值
//赋值
Status AssignList_Sq(SqList &L)
{
int n,m; //输入个数
printf("请输入集合元素个数:");
scanf("%d",&n);
for(int i = 0;i < n;i++){
printf("请输入第%d个元素:",i+1);
scanf("%d",&m);
L.elem[i] = m;
L.length++;
}
printf("赋值成功");
}
8. 线性表的打印
//打印
void printf_Sq(SqList L)
{
if(L.elem == NULL){
printf("该顺序表已被销毁");
}
for(int i = 0; i < GetLength(L); i++){
printf("%d ",L.elem[i]);
}
printf("\n");
}
9. 用e返回线性表中第i个元素
//用e返回L中第i个元素
Status GetElem(SqList L,int i, int &e)
{
if(i < 1||i > GetLength(L))
return ERROR;
e = L.elem[i-1];
return OK;
}
10. 在表中查找第一个值与e满足compare()元素的位序
Status equal_e(int a,int b)
{
if(a==b)
return OK;
else
return ERROR;
}
//在表中查找第一个值与e满足compare()元素的位序
Status LocateElem(SqList L, int e,int (*compare)(int,int)){
int i = 1;
//int *p = L.elem;
while(i<=GetLength(L)&&!(*compare)(L.elem[i-1],e)){ //*p++
++i;
}
if(i<=GetLength(L))
return i;
else
return 0;
}
//拓展知识:函数指针
//函数指针做函数参数(回调函数)
拓展知识:函数指针(指向函数的指针)
函数指针定义方式(先定义函数类型,根据类型定义指针变量);
先定义函数指针类型,根据类型定义指针变量;
直接定义函数指针变量;
int my_func(int a,int b){
printf("ret:%d\n", a + b);
return 0;
}
//1. 先定义函数类型,通过类型定义指针
void test01(){
typedef int(FUNC_TYPE)(int, int);
FUNC_TYPE* f = my_func;
//如何调用?
(*f)(10, 20);
f(10, 20);
}
//2. 定义函数指针类型
void test02(){
typedef int(*FUNC_POINTER)(int, int);
FUNC_POINTER f = my_func;
//如何调用?
(*f)(10, 20);
f(10, 20);
}
//3. 直接定义函数指针变量
void test03(){
int(*f)(int, int) = my_func;
//如何调用
(*f)(10, 20);
f(10, 20);
}
函数指针做函数参数(回调函数)
函数参数除了是普通变量,还可以是函数指针变量。
//形参为普通变量
void fun(int x ){}
//形参为函数指针变量
void fun(int(*p)(int a)){}
函数指针变量常见的用途之一是把指针作为参数传递到其他函数,指向函数的指针也可以作为参数,以实现函数地址的传递。
11. 获取顺序表指定元素的后继
//获取顺序表指定元素的后继
Status Next_elem(SqList L,int i,int &e){
if(i<1||i>L.length){
return ERROR;
}
if(i==GetLength(L)){
printf("最后一个元素没有后继");
return ERROR;
}
e = L.elem[i];
}
12. 获取顺序表指定元素的前驱
//获取顺序表指定元素的前驱
Status Prior_elem(SqList L,int i,int &e){
if(i<1||i>L.length){
return ERROR;
}
if(i==1){
printf("第一个元素没有前驱");
return ERROR;
}
e = L.elem[i-2];
}
13. 插入算法实现
//在顺序表中插入指定的元素
Status ListInsert_Sq(SqList &L,int i,int e){
if(i<1||i>GetLength(L)+1)
return ERROR;
if(GetLength(L)>=L.listsize){
int *newspace = (int*)realloc(L.elem,(L.listsize+LISTINCREMENT)*sizeof(int)); //重新分配内存空间
if(!newspace){
exit(OVERFLOW);
}
L.elem = newspace;
L.listsize+=LISTINCREMENT;
}
//书上的
// int *q,*p;
// q = &(L.elem[i-1]);
// for(p=&(L.elem[L.length-1]);p>=q;p--)
// *(p+1)=*p;
// *q=e;
// ++L.length;
// return OK;
int k,j;
for(k = 0,j=L.length-1;j>=k;k++,j--){
L.elem[j+1] = L.elem[j];
}
L.elem[k] = e;
++L.length;
return OK;
}
考虑移动元素的平均情况:
假设在第 i 个元素之前插入的概率为,则在长度为n 的线性表中插入一个元素所需移动元素次数的期望值为:
在这里插入代码片
若假定在线性表中任何一个位置上进行插入的概率都是相等的,则移动元素的期望值为:
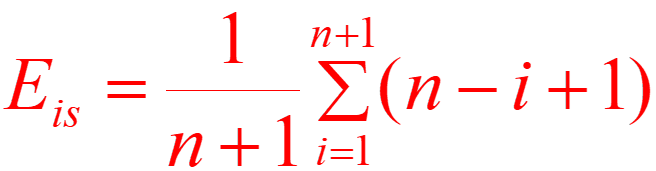
14. 删除算法实现
//删除顺序表指定位置元素
Status DeleteList_Sq(SqList &L,int i,int &e)
{
int j=0;
if(i<1||i>L.length)
{
return ERROR;;
}
else
{
e = L.elem[i-1];
for(j=i; j<=L.length-1; j++)
{
L.elem[j-1]=L.elem[j];
}
--L.length;
}
}
考虑移动元素的平均情况:
假设删除第 i 个元素的概率为, 则在长度为n 的线性表中删除一个元素所需移动元素次数的期望值为:

若假定在线性表中任何一个位置上进行删除的概率都是相等的,则移动元素的期望值为:


15. 并集
//并集A+B
Status union_set(SqList La,SqList Lb,SqList &Lc){
int La_Len = GetLength(La);
int Lb_Len = GetLength(Lb);
int e;
for(int i=1;i<=Lb_Len;i++){
GetElem(Lb,i,e);
if(!LocateElem(La,e,equal_e))
ListInsert_Sq(La,++La_Len,e);
}
for(int i =0;i<=La_Len;i++){
GetElem(La,i,e);
ListInsert_Sq(Lc,i,e);
}
}
16. 交集
//交集AB
Status mixture_set(SqList La,SqList Lb,SqList &Lc){
int La_Len = GetLength(La);
int Lb_Len = GetLength(Lb);
int e;
int index = 0;
SqList p,q;
if(La_Len >= Lb_Len){
p = Lb;
q = La;
}
else{
p = La;
q = Lb;
}
//p = La_len <= Lb_len ? La:Lb;
//q = La_len > Lb_len ? La:Lb;
for(int i=1;i<=GetLength(p);i++){
GetElem(p,i,e);
if(LocateElem(q,e,equal_e))
ListInsert_Sq(Lc,++index,e);
}
if(GetLength(Lc))
return OK;
else
return ERROR;
}
17. 差集
//差集A-B
Status different(SqList La,SqList Lb,SqList &Lc)
{
int La_len=GetLength(La);
int e;
int index=0;
for(int i=1; i<=La_len; i++)
{
GetElem(La,i,e);
if(!LocateElem(Lb,e,equal_e))
ListInsert_Sq(Lc,++index,e);
}
if(GetLength(Lc))
return OK;
else
return ERROR;
}
18. 逆转
//逆转
Status ReverseList_Sq(SqList &L){
int mid = (L.length-1)/2;
for(int i=0; i<=mid; i++){
int tmp = L.elem[i];
L.elem[i] = L.elem[L.length-1-i];
L.elem[L.length-1-i] = tmp;
}
}
