基本介绍
选择排序(select sorting)也属于内部排序法,是从欲排序的数据中,按指定的规则选出来某个元素,再依规定交换位置后达到排序的目的。
它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
基本思想
选择排序(select sorting)也是一种简单直观的排序方法。
基本思想为:
注:n 是数组大小
- 第一次从
arr[0]~arr[n-1]中选取最小值,与 arr[0] 交换 - 第二次从
arr[1]~arr[n-1]中选取最小值,与 arr[1] 交换 - 第 i 次从
arr[i-1]~arr[n-1]中选取最小值,与 arr[i-1] 交换 - 依次类推,总共通过
n - 1次,得到一个按排序码从小到大排列的有序序列
思路分析
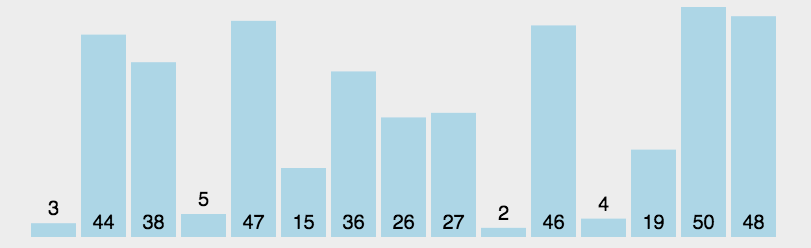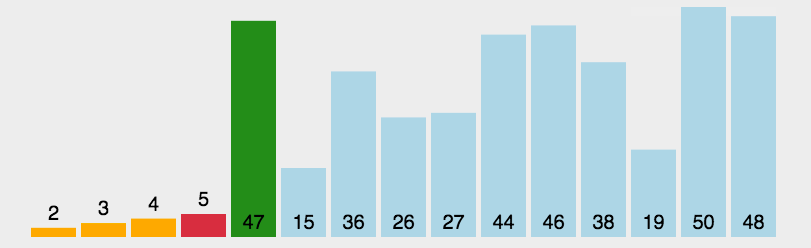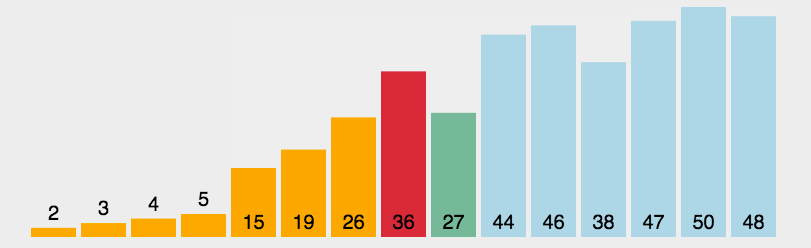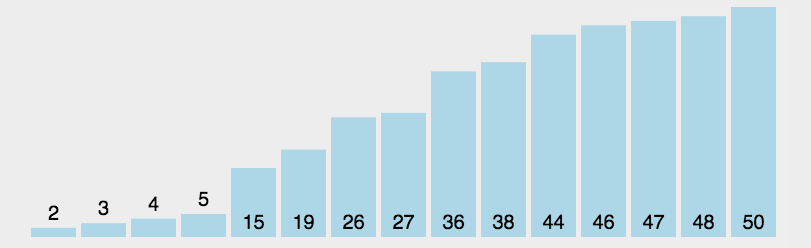
动图:
说明:
1.选择排序一共有数组大小 - 1 轮排序
2.每 1 轮排序,又是一个循环,循环的规则
①先假定当前这轮循环的第一个数是最小数
②然后和后面每个数进行比较,如果发现有比当前数更小的数,则重新确定最小数,并得到下标
③当遍历到数组的最后时,就得到本轮最小的数
④和当前循环的第一个数进行交换
代码实现
要求:假设有一群牛,颜值分别是 101,34,119,1 ,请使用选中排序从低到高进行排序
演变过程
使用逐步推导的方式,进行讲解排序,容易理解。
推导每一步的演变过程,便于理解。
这是一个很重要的思想:
一个算法:先简单 --> 做复杂:
就是可以把一个复杂的算法,拆分成简单的问题 -> 逐步解决
@Test
public void processDemo() {
int arr[] = {101, 34, 119, 1};
System.out.println("原始数组:" + Arrays.toString(arr));
processSelectSort(arr);
}
public void processSelectSort(int[] arr) {
// 第 1 轮:
// 原始数组:101, 34, 119, 1
// 排序后: 1, 34, 119, 101
int min = arr[0]; // 先假定第一个数为最小值
int minIndex = 0;
for (int j = 0 + 1; j < arr.length; j++) {
// 挨个与最小值对比,如果小于,则进行交换
if (min > arr[j]) {
// 如果后面的值比当前的 min 小,则重置min为这个数
min = arr[j];
minIndex = j;
}
}
// 第 1 轮结束后,得到了最小值
// 将这个最小值与 arr[0] 交换
arr[minIndex] = arr[0];
arr[0] = min;
System.out.println("第 1 轮排序后:" + Arrays.toString(arr));
// 第 2 轮
// 当前数组:1, 34, 119, 101
// 排序后: 1, 34, 119, 101
min = arr[1];
minIndex = 1;
// 第二轮,与第 3 个数开始比起
for (int j = 0 + 2; j < arr.length; j++) {
// 挨个与最小值对比,如果小于,则进行交换
if (min > arr[j]) {
// 如果后面的值比当前的 min 小,则重置min为这个数
min = arr[j];
minIndex = j;
}
}
// 第 2 轮结束后,得到了最小值
// 将这个最小值与 arr[1] 交换
arr[minIndex] = arr[1];
arr[1] = min;
System.out.println("第 2 轮排序后:" + Arrays.toString(arr));
// 第 3 轮
// 当前数组:1, 34, 119, 101
// 排序后: 1, 34, 101, 119
min = arr[2];
minIndex = 2;
// 第二轮,与第 4 个数开始比起
for (int j = 0 + 3; j < arr.length; j++) {
// 挨个与最小值对比,如果小于,则进行交换
if (min > arr[j]) {
// 如果后面的值比当前的 min 小,则重置min为这个数
min = arr[j];
minIndex = j;
}
}
// 第 3 轮结束后,得到了最小值
// 将这个最小值与 arr[2] 交换
arr[minIndex] = arr[2];
arr[2] = min;
System.out.println("第 3 轮排序后:" + Arrays.toString(arr));
}
测试输出
原始数组:[101, 34, 119, 1]
第 1 轮排序后:[1, 34, 119, 101]
第 2 轮排序后:[1, 34, 119, 101]
第 3 轮排序后:[1, 34, 101, 119]
从上述的演变过程来看,发现了规律:循环体都是相同的,只是每一轮排序所假定的最小值的下标在递增。因此可以改写成如下方式
@Test
public void processDemo2() {
int arr[] = {101, 34, 119, 1};
System.out.println("原始数组:" + Arrays.toString(arr));
processSelectSort2(arr);
}
public void processSelectSort2(int[] arr) {
// 把之前假定当前最小值的地方,使用变量 i 代替了
// 由于需要 arr.length -1 轮,所以使用外层一个循环,就完美的解决了这个需求
for (int i = 0; i < arr.length - 1; i++) {
int min = arr[i]; // 先假定第一个数为最小值
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
// 挨个与最小值对比,如果小于,则进行交换
if (min > arr[j]) {
// 如果后面的值比当前的 min 小,则重置min为这个数
min = arr[j];
minIndex = j;
}
}
// 第 i 轮结束后,得到了最小值
// 将这个最小值与 arr[i] 交换
arr[minIndex] = arr[i];
arr[i] = min;
System.out.println("第 " + (i + 1) + " 轮排序后:" + Arrays.toString(arr));
}
}
测试输出
原始数组:[101, 34, 119, 1]
第 1 轮排序后:[1, 34, 119, 101]
第 2 轮排序后:[1, 34, 119, 101]
第 3 轮排序后:[1, 34, 101, 119]
由此可以得到,选择排序的时间复杂度是 o(n²),因为是一个嵌套 for 循环
结果是一样的,但是你会发现,在第 1 轮和第 2 轮的序列是一样的,但是代码中目前也进行了交换,可以优化掉这一个点
优化
public void processSelectSort2(int[] arr) {
// 把之前假定当前最小值的地方,使用变量 i 代替了
// 由于需要 arr.length -1 轮,所以使用外层一个循环,就完美的解决了这个需求
for (int i = 0; i < arr.length - 1; i++) {
int min = arr[i]; // 先假定第一个数为最小值
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
// 挨个与最小值对比,如果小于,则进行交换
if (min > arr[j]) {
// 如果后面的值比当前的 min 小,则重置min为这个数
min = arr[j];
minIndex = j;
}
}
// 第 i 轮结束后,得到了最小值
// 将这个最小值与 arr[i] 交换
//但如果minIndex没有改变,也就是最小值未发生改变,则不需要执行后面的交换了
if (minIndex != i) {
arr[minIndex] = arr[i];
arr[i] = min;
}
System.out.println("第 " + (i + 1) + " 轮排序后:" + Arrays.toString(arr));
}
}
测试输出
原始数组:[101, 34, 119, 1]
第 1 轮排序后:[1, 34, 119, 101]
第 3 轮排序后:[1, 34, 101, 119]
则可以看到,第二轮就跳过了交换这一个步骤,从而优化了这个算法所要花费的时间。
算法函数封装
@Test
public void selectSortTest() {
int arr[] = {101, 34, 119, 1};
System.out.println("升序");
System.out.println("原始数组:" + Arrays.toString(arr));
selectSort(arr, true);
System.out.println("排序后:" + Arrays.toString(arr));
System.out.println("降序");
System.out.println("原始数组:" + Arrays.toString(arr));
selectSort(arr, false);
System.out.println("排序后:" + Arrays.toString(arr));
}
/**
* 选择排序算法封装
*
* @param arr 要排序的数组
* @param asc 升序排列,否则降序
*/
public void selectSort(int[] arr, boolean asc) {
// 把之前假定当前最小值的地方,使用变量 i 代替了
// 由于需要 arr.length -1 轮,所以使用外层一个循环,就完美的解决了这个需求
for (int i = 0; i < arr.length - 1; i++) {
int current = arr[i]; // 先假定第一个数为最小值
int currentIndex = i;
for (int j = i + 1; j < arr.length; j++) {
// 挨个与最小值对比,如果小于,则进行交换
if (asc) {
if (current > arr[j]) {
// 如果后面的值比当前的 min 小,则重置min为这个数
current = arr[j];
currentIndex = j;
}
} else {
if (current < arr[j]) {
// 如果后面的值比当前的 min 大,则重置为这个数
current = arr[j];
currentIndex = j;
}
}
}
// 第 i 轮结束后,得到了最小/大值
// 将这个值与 arr[i] 交换
//但如果minIndex没有改变,也就是最小值未发生改变,则不需要执行后面的交换了
if (currentIndex == i) {
arr[currentIndex] = arr[i];
arr[i] = current;
}
}
}
测试输出
升序
原始数组:[101, 34, 119, 1]
排序后:[1, 34, 101, 119]
降序
原始数组:[1, 34, 101, 119]
排序后:[119, 101, 34, 1]
大量数据耗时测试
排序随机生成的 8 万个数据
@Test
public void bulkDataSort() {
int max = 80_000;
int[] arr = new int[max];
for (int i = 0; i < max; i++) {
arr[i] = (int) (Math.random() * 80_000);
}
Instant startTime = Instant.now();
selectSort(arr, true);
// System.out.println(Arrays.toString(arr));
Instant endTime = Instant.now();
System.out.println("共耗时:" + Duration.between(startTime, endTime).toMillis() + " 毫秒");
}
多次运行测试输出
共耗时:2983 毫秒
共耗时:3022 毫秒
冒泡排序和选择排序的时间复杂度虽然都是 o(n²),但由于冒泡排序每一步有变化都要交换位置,导致了消耗了大量的时间,所以选择排序相对冒泡排序所花费的时间要更少。
关于冒泡排序请看java 排序算法之冒泡排序
到此这篇关于java 排序算法之选择排序的文章就介绍到这了,更多相关java 选择排序内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!