【苏州程序大白用2万字】解析数据结构和八大排序算法☀️《❤️记得收藏❤️》

️‍开讲啦！！！！️‍苏州程序大白️‍

1、算法的时间复杂度

1.2、评判程序优劣的方法

• 消耗计算机资源和执行效率

• 计算算法执行的耗时

• 时间复杂度（推荐）

1.3、时间复杂度

• 评判标准：量化算法执行的操作/执行步骤的数量

• 最重要的项：时间复杂度表达式最有意义的项

• 大O记法对时间复杂度进行表示：O(量化表达式中最有意义的项)

def sumofN(n):
    theSum = 0
    for i in range(1, n+1):
        theSum = thSum + i
    return theSum

print(sumofN(10))
# 1 + n + 1  =====>   n + 2  =====>  O(n)
a = 5
b = 6
c = 10
for i in range(n):
    for j in range(n):
    	x = i * i
    	y = j * j
    	z = i * j
for k in range(n):
    w = a * k + 45
    v = b * b
d = 33

# 3 + 3n**2 + 2n + 1 ====> 3n**2 + 2n ====> 3n**2 ====> n**2 ====> O(n**2)

1.4、常见的时间复杂度

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)

2、栈

• 特性：先进先出

• 应用：每个 web 浏览器都有一个返回按钮。当你浏览网页时，这些网页被放置在一个栈中（实际是网页的网址）。你现在查看的网页在顶部，你第一个查看的网页在底部。如果按‘返回’按钮，将按相反的顺序浏览刚才的页面。

2.1、用python实现一个简单的栈

需要实现的方法

- Stack() //创建一个空的新栈。 它不需要参数，并返回一个空栈。
- push(item)    //将一个新项添加到栈的顶部。它需要 item 做参数并不返回任何内容。
- pop()   //从栈中删除顶部项。它不需要参数并返回 item 。栈被修改。
- peek()   //从栈返回顶部项，但不会删除它。不需要参数。 不修改栈。
- isEmpty()  //测试栈是否为空。不需要参数，并返回布尔值。
- size()   //返回栈中的 item 数量。不需要参数，并返回一个整数。
class Stark():
    def __init__(self):
        self.items = []
    def push(self, item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
	def peek(self):
        return len(self.items) - 1
    def isEmpty(self):
        return self,items == []
    def size(self):
        return len(self.items)

3、队列

• 特性：先进先出

• 应用场景：

我们的计算机实验室有 30 台计算机与一台打印机联网。当学生想要打印时，他们的打印任务与正在等待的所有其他打印任务“一致”。第一个进入的任务是先完成。如果你是最后一个，你必须等待你前面的所有其他任务打印。

3.1、实现一个简单的队列

- Queue() //创建一个空的新队列。 它不需要参数，并返回一个空队列。
- enqueue(item) //将新项添加到队尾。 它需要 item 作为参数，并不返回任何内容。
- dequeue() //从队首移除项。它不需要参数并返回 item。 队列被修改。
- isEmpty() //查看队列是否为空。它不需要参数，并返回布尔值。
- size() //返回队列中的项数。它不需要参数，并返回一个整数。
class Queue():
    def __init__(self):
        self.items = []
    def enqueue(self, item):
        self.items.insert(0, item)
    def dequeue(self):
        return self.items.pop()
    def isEmpty(self):
        return self.items == []
    def size(self):
        return len(self.items)

3.2、应用（烫手的山芋）

//案例：烫手的山芋
// 烫手山芋游戏介绍：6个孩子围城一个圈，排列顺序孩子们自己指定。第一个孩子手里有一个烫手的山芋，需要在计时器计时1秒后将山芋传递给下一个孩子，依次类推。规则是，在计时器每计时7秒时，手里有山芋的孩子退出游戏。该游戏直到剩下一个孩子时结束，最后剩下的孩子获胜。请使用队列实现该游戏策略，排在第几个位置最终会获胜。
// 准则：队头孩子的手里永远要有山芋。
queue = Queue()
kids = ['A','B','C','D','E','F']
for kid in kids:
    queue.enqueue(kid)
while queue.size() > 1:
    for i in range(6):
        kid = queue.dequeue()
        queue.enqueue(kid)
    queue.dequeue()
    
print('获胜者为：', queue.dequeue())

3.3、双端队列

同队列相比，有两个头部和尾部。可以在双端进行数据的插入和删除，提供了单数据结构中栈和队列的特性

- Deque() //创建一个空的新 deque。它不需要参数，并返回空的 deque。
- addFront(item) //将一个新项添加到 deque 的首部。它需要 item 参数 并不返回任何内容。
- addRear(item) //将一个新项添加到 deque 的尾部。它需要 item 参数并不返回任何内容。
- removeFront() //从 deque 中删除首项。它不需要参数并返回 item。deque 被修改。
- removeRear() //从 deque 中删除尾项。它不需要参数并返回 item。deque 被修改。
- isEmpty() //测试 deque 是否为空。它不需要参数，并返回布尔值。
- size() //返回 deque 中的项数。它不需要参数，并返回一个整数。
class Dequeue():
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items == []
    def size(self):
        return len(self.items)
    def addFront(self, item):
        self.items.append(item)
    def addRear(self, item):
        self.items.insert(0, item)
    def removeFront(self):
        return self.items.pop()
    def removeRear(self):
        return self.items.pop(0)

案例：回文检查

回文是一个字符串，读取首尾相同的字符，例如，radar toot madam

def isHuiWen(s):
    ex = True
    
    q = Dequeue()
    
    for ch in s:
        q.addFront(ch)
        
    for i in range(len(s)//2):
        font = q.removeFront()
        rear = q.removeRear()
        if font != rear:
            ex = False
            break
    return ex
print(isHuiWen('addan'))

4、链表和顺序表

4.1、顺序表

• 集合中存储的元素是有顺序的，顺序表的结构可以分为两种形式：单数据类型和多数据类型。

• python中的列表和元组就属于多数据类型的顺序表。

• 顺序表的弊端：顺序表的结构需要预先知道数据大小来申请连续的存储空间，而在进行扩充时又需要进行数据的搬迁。

4.2、链表

• 相对于顺序表，链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理且进行扩充时不需要进行数据搬迁。

• 链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是不像顺序表一样连续存储数据，而是每一个结点（数据存储单元）里存放下一个结点的信息（即地址）。

4.3、构造链表

is_empty()：//链表是否为空

length()：//链表长度

travel()：//遍历整个链表

add(item)：//链表头部添加元素

append(item)：//链表尾部添加元素

insert(pos, item)：//指定位置添加元素

remove(item)：//删除节点

search(item)：//查找节点是否存在

节点

class Node():
    def __init__(self,item):
        self.item = item
        self.next = None

链表

class Link():
    # 构建一个空链表
    def __init__(self):
        self._head = None // 永远指向链表中的头节点
    # 向链表的头部插入节点
    def add(self, item):
        node = Node(item)
        node.next = self._head
        self._head = node
    def travel(self):
        cur = self._head
        # 链表为空则输出“链表为空”
        if self._head = None:
            print("链表为空")
        while cur:
            print(cur.item)
            cur = cur.next
    def isEmpty(self):
        return self._head == None
    def length(self):
        cur = self._head
        count = 0
        while cur:
            count += 1
            cur = cur.next
        return count
    def search(self, item):
        cur = self._head
        find = False
        while cur:
            if cur.item == item:
                find = True
                break
            cur = cur.next
        return find
    
    def append(self, item):
        node = Node(item)
        if self._head == None:
            self._head = node
            return
        
        cur = self._head
        pre = None
        while cur:
            pre = cur
            cur = cur.next
        pre.next = node
    def insert(self, pos, item):
        node = Node(item)
        
        if pos < 0 or pos > self.length():
            print("重新给pos赋值")
            
        cur = self._head
        pre = None
        
        for i in range(pos):
            pre = cur
            cur = cur.next
        pre.next = node
        node.next = cur
    def remove(self, item):
        cur = self._head
        pre = None
        
        if self._head == None:
            print("链表为空，没有可删除的节点")
            return
        
        # 删除的是第一个节点的情况
        if self._head.item == item:
            self._head = self._head.next
            return
        
        # 删除的不是第一个节点的情况
        while cur:
            pre = cur
            cur = cur.next
            if cur.item == item:
                pre.next = cur.next
                return

5、顺序查找

• 当数据存储在诸如列表的集合中时，我们说这些数据具有线性或顺序关系。 每个数据元素都存储在相对于其他数据元素的位置。 由于这些索引值是有序的，我们可以按顺序访问它们。 这个过程产实现的搜索即为顺序查找。

顺序查找原理剖析：

• 从列表中的第一个元素开始，我们按照基本的顺序排序，简单地从一个元素移动到另一个元素，直到找到我们正在寻找的元素或遍历完整个列表。如果我们遍历完整个列表，则说明正在搜索的元素不存在。

• 代码实现：该函数需要一个列表和我们正在寻找的元素作为参数，并返回一个是否存在的布尔值。found 布尔变量初始化为 False，如果我们发现列表中的元素，则赋值为 True。

• 有序列表：之前我们列表中的元素是随机放置的，因此在元素之间没有相对顺序。如果元素以某种方式排序，顺序查找会发生什么？我们能够在搜索技术中取得更好的效率吗？

二分查找：一定是只可以被应用在有序列表中

• 有序列表对于我们的实现搜索是很有用的。在顺序查找中，当我们与第一个元素进行比较时，如果第一个元素不是我们要查找的，则最多还有 n-1 个元素需要进行比较。 二分查找则是从中间元素开始，而不是按顺序查找列表。 如果该元素是我们正在寻找的元素，我们就完成了查找。 如果它不是，我们可以使用列表的有序性质来消除剩余元素的一半。如果我们正在查找的元素大于中间元素，就可以消除中间元素以及比中间元素小的一半元素。如果该元素在列表中，肯定在大的那半部分。然后我们可以用大的半部分重复该过程，继续从中间元素开始，将其与我们正在寻找的内容进行比较。

5.1、二分查找实现

def sort(alist, item):  // item就是我们要找的元素
    low = 0  //进行二分查找操作的列表中的第一个元素的下标
    high = len(alist)
    find = False
    
    while low <= high:
        mid = (low+high) // 2 # 中间元素的下标
        if item > alist[mid]: // 我们要找的数比中间的数大，则意味着我们要找的数在中间元素的右侧
            low = mid + 1
        elif item < alist[mid]: // 我们要找的数比中间的数小，则我们要找的数在中间数的左侧
            high = mid - 1
        else:
            find = True
            break
    return find

• test

alist = [1,2,3,4,5,6,7]
print(sort(alist, 51))

output:  False

6、二叉树

• 根节点

• 左叶子节点

• 右叶子节点

• 子树

• 高度

6.1、二叉树的遍历

• 广度遍历：逐层遍历

• 深度遍历

• 前序：根左右

• 中序：左根右

• 后序：左右根

6.2、构造普通二叉树

class Node():
    def __init__(self, item):
        self.item = item
        self.left = None
        self.right = None
class Tree():
    # 构造出一颗空的二叉树
    def __init__(self, item): // root指向第一个节点的地址，如果root指向了None，则意味着该二叉树为空
        self.root = None
    # 向二叉树中插入节点
    def addNode(self, item):
        node = Node(item)
        if self.root == None:
            # addNode如果第一次被调用则意味着：向空树中插入第一个节点，该节点一定是该树的根节点
            self.root = node
            return
        # 如果上面的if不执行则树为非空，下面就执行向一个非空的树中插入节点的操作
        cur = self.root
        queue = [cur]
        while queue:
            n = queue.pop(0)
            if n.left != None:
                queue.append(n.left)
            else:
                n.left = node
                break
            if n.right != None:
                queue.append(n.right)
            else:
                n.right = node
                break
    def travel(self):
        # 如果为空
        if self.root == None:
            print("树为空！")
            return
        
        cur = self.root
        queue = [cur]
        while queue:
            n = queue.pop(0)
            print(n.item)
            if n.left != None:
                queue.append(n.left)
            if n.right != None:
                queue.append(n.right)
    # 前序遍历
    def forward(self, root):
        if root == None:
            return
        
        print(root.item)
        self.forward(root.left)
        self.forward(root.right)
        
    # 中序遍历
    def middle(self, root):
        if root == None:
            return
        self.middle(root.left)
        print(root.item)
        self.middle(root.right)
        
    # 后序遍历
    def back(self, root):
        if root == None:
            return
        self.back(root.left)
        self.back(root.right)
        print(root.item)

6.3、构造排序二叉树

class Node():
    def __init__(self, item):
        self.item = item
        self.left = None
        self.right = None
class SortTree():
    def __init__(self):
        self.root = None
    def insertNode(self, item):
        node = Node(item)
        # 向空树插入第一个节点
        if self.root == None:
            self.root = node
            return
        # 树为非空的情况
        cur = self.root
        
        while True:
            if node.item > cur.item: // 往右插
                if cur.right == None:
                    cur.right = node
                    break
                else:
                    cur = cur.right
            else: #往左插
                if cur.left = None:
                    cur.left = node
                    break
                else:
                    cur = cur.left
    
    def forward(self, root):
        if root == None:
            return
        print(root.item)
        self.forward(root.left)
        self.forward(root.right)
        
    def middle(self, root):
        if root == None:
            return
        
        self.middle(root.left)
        print(root.item)
        self.middle(root.right)
    
    def back(self, root):
        if root == None:
            return
        
        self.back(root.left)
        self.back(root.right)
        print(root.item)

7、八大排序算法实现与讲解

7.1、冒泡排序

主要思路：

1、比较相邻的元素，根据规则选择是否交换这两个数

2、从开始第一对到结尾最后一对

3、针对多个元素重复以上操作（除了最后一个）

• 时间复杂度：平均O(n^2) 最好：O(n)

• 空间复杂度：O(1)

• 稳定性：稳定
  
  C代码实现：

void bubble_sort(int *arr,int len)
{
     
    int i,j,tmp;
    int swap = 1;
    for(i = 0; i< len-1;i++)
    {
     
        for(j = 0; j< len -1 -i; j++)
            if(arr[j] > arr[j+1])
            {
     
                tmp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = tmp;
                swap = 0;
            }
        if(swap)	//如果没进行交换直接退出
            return;
    }
}

Python代码实现：

def bubble_sort(arr:[int])-> [int]:
    swap = True
    for i in range(0,len(arr)-1):
        for j in range(0,len(arr)-1-i):
            if arr[j] > arr[j+1]:
                arr[j],arr[j+1] = arr[j+1],arr[j]
                swap = False
        if swap:
            return arr
 
    return arr

7.2、简单选择排序

主要思路：每趟从待排序的记录中选出关键字最小的记录，顺序放在已排序的记录序列末尾，直到全部排序结束为止。

• 时间复杂度：O(n^2)

• 空间复杂度：O(1)

• 稳定性：不稳定
  
  C代码实现：

void select_sort(int *arr,int len)
{
     
    int i,j,tmp;
    int min;
    for(i = 0;i<len;i++)
    {
     
        min = i;
        for(j=i + 1;j<len;j++)
            if(arr[j] < arr[min])
                min = j;
        tmp = arr[i];
        arr[i]=arr[min];
        arr[min] = tmp;
    }
}

Python代码实现：

def select_sort(arr:[int])-> [int]:
    for i in range(0,len(arr)):
        min_index = i
        for j in range(i+1,len(arr)):
            if arr[min_index] > arr[j]:
                min_index = j
        arr[min_index],arr[i] = arr[i],arr[min_index]
    return arr

7.3、插入排序

主要思路：每一趟将一个待排序的记录，按照其关键字的大小插入到有序队列的合适位置里，直到全部插入完成。

• 时间复杂度：平均:O(n^2) 最好:O(n)

• 空间复杂度：O(1)

• 稳定性：稳定

C代码实现：

void insert_sort(int *arr,int len)
{
     
    int i,j;
    int tmp = 0;
    for(i = 1;i< len;i++)
    {
     
        tmp  = arr[i];
        for(j = i-1;j>=0;j--)
            if(arr[j] > tmp)
                arr[j+1] = arr[j];
            else
                break;
        arr[j+1] = tmp;
 
    }
}

Python代码实现：

def insert_sort(arr:[int])-> [int]:
    for i in range(1,len(arr)):
        tmp = arr[i]
        j = i - 1
        while j>=0 and arr[j] > tmp:
            arr[j+1] = arr[j]
            j = j - 1
        arr[j+1] = tmp
    return arr

7.4、希尔排序（特殊的插入排序）

希尔(Shell)排序又称为缩小增量排序，它是一种插入排序。它是直接插入排序算法的一种改进版。希尔排序的比较次数和移动次数都要比直接插入排序少，当N越大时，效果越明显。

算法思想：

我们举个例子来描述算法流程（以下摘自维基百科）：

假设有这样一组数 {13, 14, 94, 33, 82, 25, 59, 94, 65, 23, 45, 27, 73, 25, 39, 10}，如果我们以步长为 5 开始进行排序：

排序前	排序后
13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10	10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45

将上述四行数字，依序接在一起时我们得到：{10, 14, 73, 25, 23, 13, 27, 94, 33, 39, 25, 59, 94, 65, 82, 45}，然后再以 3 为步长：

排序前	排序后
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45	10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94

最后以 1 为步长进行排序（此时就是简单的插入排序了）。

可想而知，步长的选择是希尔排序的重要部分。算法最开始以一定的步长进行排序，然后会继续以更小的步长进行排序，最终算法以步长为 1 进行排序。当步长为 1 时，算法变为直接插入排序，这就保证了数据一定会被全部排序。

• 时间复杂度：平均:O(nlogn) 最坏:O(n^2)

• 空间复杂度：O(1)

• 稳定性：不稳定

C代码实现：

void shell_sort(int *arr,int len,int gap)
{
     
    int tmp;
    int i,j;
    for(i = gap; i<len; i = i+gap)
    {
     
        tmp = arr[i];
        for(j = i -gap;j>=0;j=j-gap)
            if(arr[j] > tmp)
                arr[j+gap] = arr[j];
            else
                break;
        arr[j+gap] = tmp;
    }
}
 
void Shell(int *arr,int len)
{
     
    int gap[] = {
     5,3,1};    //可以分为步长的一半，这里就自定义好了
    int len_gap = sizeof(gap)/sizeof(gap[0]);
    for(int i=0;i<len_gap;++i)
        shell_sort(arr,len,gap[i]);
}

Python代码实现：

def shell_sort(arr:[int])->[int]:
    g = [5,3,1]
    for gap in g:
        for i in range(gap,len(arr)):
            tmp = arr[i]
            j = i-gap
            while j>=0 and arr[j] > tmp:
                arr[j+gap] = arr[j]
                j = j - gap
            arr[j+gap] = tmp
    return arr 

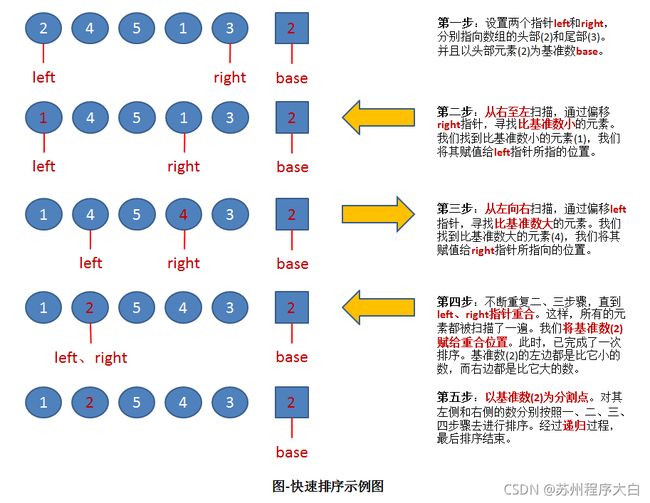
7.5、快速排序

快速排序的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分：分割点左边都是比它小的数，右边都是比它大的数。

• 时间复杂度：平均:O(nlogn) 最坏:O(n^2)

• 空间复杂度：O(logn)

• 稳定性：不稳定

然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

C代码实现：

int division(int *arr,int left,int right)
{
     
    //每次取基准数为最左边的那个数
    int base = arr[left];
    while(left<right)
    {
     
        //从右端开始，向左寻找，找到小于基准数的值时将元素放最左边
        while(left<right && arr[right] >= base)
            --right;
        arr[left] = arr[right];
        //同理，当找到时转为左边开始向右找，将大于基准数的值放元素右边
        while(left<right && arr[left] <= base)
            ++left;
        arr[right] = arr[left];
    }
    // 最后将base放到left位置。此时，left位置的左侧数值应该都比left小；
    // 而left位置的右侧数值应该都比left大
    arr[left] = base;
    return left;
}
 
void quick_sort(int *arr,int left,int right)
{
     
    //左下标要小于右下标，否则会越界
    if( left < right)
    {
     
        //按照基准数对数组进行分割
        int base = division(arr,left,right);
        //分别对左右两边进行递归
        quick_sort(arr,left,base-1);
        quick_sort(arr,base+1,right);
    }
}
 

Python代码实现：

def quick_sort(arr:[int],left:int,right:int)->[int]:
    def division(arr:[int],left:int,right:int):
        base = arr[left]
        while left < right:
            while left < right and arr[right] >= base:
                right -= 1
            arr[left] = arr[right]
            while left < right and arr[left] <= base:
                left += 1
            arr[right] = arr[left]
        arr[left] = base
        return left
 
    if(left<right):
        base = division(arr,left,right)
        quick_sort(arr,left,base-1)
        quick_sort(arr,base+1,right)
    return arr

7.6、堆排序

堆排序是一种选择排序。

堆是一棵顺序存储的完全二叉树。

• 其中每个结点的关键字都不大于其孩子结点的关键字，这样的堆称为小根堆。

• 其中每个结点的关键字都不小于其孩子结点的关键字，这样的堆称为大根堆。

举例来说，对于n个元素的序列{R0, R1, … , Rn}当且仅当满足下列关系之一时，称之为堆：

• Ri <= R2i+1 且 Ri <= R2i+2 (小根堆)

• Ri >= R2i+1 且 Ri >= R2i+2 (大根堆)

其中i=1,2,…,n/2向下取整；

• 时间复杂度：O(nlogn)

• 空间复杂度：O(1)

• 稳定性：不稳定

7.7、归并排序

该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而 治(conquer) 的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

• 时间复杂度：O(nlog2n)

• 空间复杂度：O(n)

• 稳定性：稳定

7.8、基数排序

基本思想：将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。

算法步骤：

• 将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。

• 从最低位开始，依次进行一次排序。

• 这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

基数排序的方式可以采用 LSD（Least significant digital）或 MSD（Most significant digital），LSD 的排序方式由键值的最右边开始，而 MSD 则相反，由键值的最左边开始。

不妨通过一个具体的实例来展示一下基数排序是如何进行的。 设有一个初始序列为: R {50, 123, 543, 187, 49, 30, 0, 2, 11, 100}。

我们知道，任何一个阿拉伯数，它的各个位数上的基数都是以 0~9 来表示的，所以我们不妨把 0~9 视为 10 个桶。

我们先根据序列的个位数的数字来进行分类，将其分到指定的桶中。例如：R[0] = 50，个位数上是 0，将这个数存入编号为 0 的桶中。

分类后，我们在从各个桶中，将这些数按照从编号 0 到编号 9 的顺序依次将所有数取出来。这时，得到的序列就是个位数上呈递增趋势的序列。

按照个位数排序： {50, 30, 0, 100, 11, 2, 123, 543, 187, 49}。

接下来，可以对十位数、百位数也按照这种方法进行排序，最后就能得到排序完成的序列。

• 时间复杂度：O(dn)

• 空间复杂度：O(n)

• 稳定性：稳定
  

8、作者相关的文章、资源分享

让天下没有学不会的技术
学习C#不再是难问题
《C#入门到高级教程》
有关C#实战项目
C#RS232C通讯源码
C#委托数据传输
C# Modbus TCP 源代码
C# 仓库管理系统源码
C# 欧姆龙通讯Demo
C# 欧姆龙通讯Demo
2021C#与Halcon视觉通用的框架
✨有关C#项目欢迎各位查看个人主页✨

机器视觉、深度学习
《Halcon入门到精通》
《深度学习资料与教程》
有关机器视觉、深度学习实战
2021年C#+HALCON视觉软件
2021年C#+HALCON实现模板匹配
C#集成Halcon的深度学习软件
C#集成Halcon的深度学习软件，带[MNIST例子]数据集
C#支持等比例缩放拖动的halcon WPF开源窗体控件
2021年Labview联合HALCON
2021年Labview联合Visionpro
基于Halcon及VS的动车组制动闸片厚度自动识别模块
✨有关机器视觉、深度学习实战欢迎各位查看个人主页✨

Java、数据库教程与项目
《JAVA入门到高级教程》
《数据库入门到高级教程》
有关Java、数据库项目实战
Java经典怀旧小霸王网页游戏机源码增强版
Java物业管理系统+小程序源码
JAVA酒店客房预定管理系统的设计与实现SQLserver
JAVA图书管理系统的研究与开发MYSQL
✨有关Java、数据库教程与项目实战欢迎各位查看个人主页✨

分享Python知识讲解、分享
《Python知识、项目专栏》
《Python 检测抖音关注账号是否封号程》
《手把手教你Python+Qt5安装与使用》
《用一万字给小白全面讲解python编程基础问答》
《Python 绘制Android CPU和内存增长曲线》
有关Python项目实战
Python基于Django图书管理系统
Python管理系统
2021年9个常用的python爬虫源码
python二维码生成器
✨有关Python教程与项目实战欢迎各位查看个人主页✨

分享各大公司面试题、面试流程
《2021年金九银十最新的VUE面试题☀️《❤️记得收藏❤️》》
《只要你认真看完一万字☀️Linux操作系统基础知识☀️分分钟钟都吊打面试官《❤️记得收藏❤️》》
《❤️用一万字给小白全面讲解python编程基础问答❤️《记得收藏不然看着看着就不见了》》
✨有关各大公司面试题、面试流程欢迎各位查看个人主页✨

️‍关注苏州程序大白，持续更新技术分享。谢谢大家支持️‍

❤️关注苏州程序大白公众号❤️