论文分享--＞GCN--＞SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS

本次要总结和分享的是ICLR2017的关于GCN方面的代表作之一论文：SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS，论文链接为 paper，参考的实现代码为pygcn

先导知识

在读这篇论文之前，需要对先导论文 Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering 有着深入的理解，否则里面数学推导会让人感到迷茫。关于该先导论文，之前的博文已经对其推导过程进行了详细分析，Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering，感兴趣可以一看，因为其数学推导过程比较复杂，下面进行下简单梳理：

1. 回顾卷积定义

   在维基百科里，可以得到卷积操作的定义：
   $(f\ast g)(t)$ 为 $f\ast g$ 的卷积

   • 连续形式
     $$(f\ast g)(t)={\int }_{R}f(x)g(t-x)dx$$
   • 离散形式
     $$(f\ast g)(t)=\sum _{R}f(x)g(t-x)$$

2. 用傅里叶变换来表示卷积

   $$f\ast g=F^{-1}\{F\{f\}\cdot F\{g\}\}$$

   $F$ 表示傅里叶变换，$F^{-1}$ 傅里叶逆变换

   也即是：即对于函数 $f$与 $g$ 两者的卷积是其函数傅立叶变换乘积的逆变换

3. 在graph上的卷积形式推导过程

   $$f\ast g=F^{-1}\{F\{f\}\cdot F\{g\}\}$$

   $$g\ast x=U((U^{T}g)\odot (U^{T}x))$$

   上式中的$g$ 表示卷积核函数（带参数），$U$ 表示是graph的邻接矩阵$A$ 的拉普拉斯矩阵$L$ 的特征向量

   由此得到图上的卷积形式：

   $$y=\sigma (U{g}_{\theta }(\Lambda )U^{T}x)$$

   其中$\sigma$ 为激活函数，$g_{\theta }(\Lambda )$ 就是卷积核，注意$\Lambda$ 为拉普拉斯矩阵$L$特征值组成的对角矩阵，所以$g_{\theta }(\Lambda )$也是对角的

   推导可得卷积核函数$g_{\theta }(\Lambda )$ 如下：
   $$g_{\theta }(\Lambda )=\sum _{k=0}^{K-1}{\theta }_k{\Lambda }^k$$

   继续推导可得：

   $$y=\sigma (\sum _{k=0}^{K-1}{\theta }_k(L{)}^{k}x)$$

   上式中$L$ 为graph的邻接矩阵A的拉普拉斯矩阵，$\theta$ 为卷积核参数。

4. 切比雪夫逼近卷积核

   $$g_{\theta }(\Lambda )=\sum _{k=0}^{K-1}{\theta }_k^{{}^{\prime }}{T}_k(\hat{\Lambda })$$

   其中$T_k(\cdot )$ 表示切比雪夫多项式，${\beta }_k$ 表示模型需要学习的参数，$\hat{\Lambda }$ 表示re-scaled的$L$ 特征值对角矩阵，进行这个shift变换的原因是Chebyshev多项式的输入要在 $[-1,1]$ 之间，因此 $\hat{\Lambda }=2\Lambda /{\lambda }_{max}-I$ (${\lambda }_{max}$ 为 $L$ 的最大特征值）

   $$y=\sigma (U{g}_{\theta }(\Lambda )U^{T}x)=\sigma (\sum _{k=0}^{K-1}{\theta }_k^{{}^{\prime }}{T}_k(\hat{L})x)$$

   $\hat{L}=2L/{\lambda }_{max}-I$

   由此可以进行递推逼近：

   $$T_0(\hat{L})=I,T_1(\hat{L})=\hat{L}$$

   $$T_k(\hat{L})=2\hat{L}{T}_{k-1}(\hat{L})-T_{k-2}(\hat{L})$$

熟悉了上述推导过程，那么对于本文要总结的论文理解起来就简单多了。

论文动机

• 考虑对图（如论文引用网络）中的节点（如文档）进行分类的问题，其中仅有一小部分节点带有label信息。这个问题可以被定义为基于图的半监督学习，其中标签信息通过某种形式的基于图的显式正则化在图上进行平滑，比如在损失函数上加上拉普拉斯正则项，但是这种做法的前提假设是：在图中相邻连接的节点可能拥有相似的标签信息，这种假设可能会现在建模能力，因为图中的边不一定连接拥有相似的节点，但可能包含额外的信息。
• 本论文所提方法，能直接对graph进行编码，避免了正则平滑，$f(\cdot )$ 作用在图的邻接矩阵上进行有监督学习，并且能学习到每个节点的embedding向量。
• 本论文受上面所提到的先导论文启发，限制切比雪夫多项式$K=1$，提出了一种可在图上进行快速卷积的模型，并且提出了$renormalizationtrick$，在数学上进行了推导，证明了该模型的合理性；同时展示了这种基于图的神经网络模型如何进行半监督的分类。

模型

该部分直接在先导知识基础上进行数学公式的推导，最终得到本论文所提的模型。

切比雪夫逼近卷积核函数

在先导知识中，卷积核可等于

$$g_{\theta }(\Lambda )=\sum _{k=0}^K{\theta }_k^{{}^{\prime }}{T}_k(\hat{\Lambda })$$

则有：
$$g_{\theta }(\Lambda )\star x\approx \sum _{k=0}^K{\theta }_k^{{}^{\prime }}{T}_k(\hat{\Lambda })x$$

图上的快速近似卷积

在切比雪夫逼近卷积核函数时，本论文中限制其切比雪夫项数$K=1$，同时进一步近似${\lambda }_{max}\approx 2$，则可得：
$$g_{{\theta }^{{}^{\prime }}}\star x\approx {\theta }_0^{{}^{\prime }}x+{\theta }_1^{{}^{\prime }}(L-I_N)x={\theta }_0^{{}^{\prime }}x-{\theta }_1^{{}^{\prime }}{D}^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}x$$

可以看出上述公式是一种线性的变换。

在 Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering 中，分析过，切比雪夫的项数就是就是图卷积的感受野，而这里限制了项数 K= 1，相当于只做了所谓的 first-order approximation，每个节点考虑其一阶邻居对他的影响。

这样做有一些好处的，比如能够缓解局部邻域结构的过度拟合问题，同时这种分层线性的计算方式，允许我们构建更深层次的模型，可以提高建模能力，比如当叠加两层的卷积时，相当于每个节点可以把 2-hops 邻居的特征加以聚合。这样就避免了k=1时只能考虑一阶邻居的影响了。

进一步的，为了限制模型参数，降低每层的计算等，令$\theta ={\theta }_0^{{}^{\prime }}=-{\theta }_1^{{}^{\prime }}$，则有：

$$g_{{\theta }^{{}^{\prime }}}\star x\approx \theta (I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}})x$$

$I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$ 的特征值在$[0,2]$ 范围来，当网络叠加更多层时，容易出现梯度消散/爆炸的问题。论文中提出了$renormalizationtrick$，即：
$$I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}->{\stackrel{\sim }{D}}^{-\frac{1}{2}}\stackrel{\sim }{A}{\stackrel{\sim }{D}}^{-\frac{1}{2}}$$
$$\stackrel{\sim }{A}=A+I_N,{\stackrel{\sim }{D}}_{ii}=\sum _j{\stackrel{\sim }{A}}_{ij}$$

注意：从数学公式的推导上看在$A+I_N$ 的基础上处理是合理的，同时从分析上看也是合理的，因为邻接矩阵$A$ 对角线为0，在卷积时，每个节点只能聚合其相邻节点特征，却忽略了自身特征，因此加上$I_N$ 本身也是有必要的。这种$+I_N$ 的操作可理解为$addselfloops$，也即增加自循环。

这种$renormalizationtrick$操作，保证了结果的对称性，同时做到了近似归一化。
$\stackrel{\sim }{A}=A+\lambda I_N$，针对不同的数据集，$\lambda$ 取值不一样，

因此卷积过程可表达为如下：

$$Z={\stackrel{\sim }{D}}^{-\frac{1}{2}}\stackrel{\sim }{A}{\stackrel{\sim }{D}}^{-\frac{1}{2}}X\theta$$

上式中 $X\in R^{N\times C}$，$N$ 为样本数量，$C$ 为输入通道数（也就是每个节点的特征向量维度），$\theta \in R^{C\times F}$ 为卷积核参数矩阵，$Z\in R^{N\times F}$ 为卷积后的矩阵。

上式可以形象的以下图表示：

半监督节点分类

上图中$C$ 表示每个输入节点的特征向量维度，$F$ 表示卷积后的feature_maps个数，多层叠加时，最后一层F为类别个数。

上面我们得到：
$$Z={\stackrel{\sim }{D}}^{-\frac{1}{2}}\stackrel{\sim }{A}{\stackrel{\sim }{D}}^{-\frac{1}{2}}X\theta$$

这里记：$\hat{A}={\stackrel{\sim }{D}}^{-\frac{1}{2}}\stackrel{\sim }{A}{\stackrel{\sim }{D}}^{-\frac{1}{2}}$，这一步可以在预处理阶段计算好，叠加两层卷积，则可以得：
$$Z=f(X,A)=softmax(\hat{A}Relu(\hat{A}X{W}^{(0)})W^{(1)})$$

上式中， $X\in R^{N\times C}$，$N$ 为样本数量，$C$ 为输入通道数（也就是每个节点的特征向量维度），$\hat{A}\in R^{N\times N}$，$W^{(0)}\in R^{C\times H}$ 为 输入层到隐藏层的参数矩阵，是模型需要学习的，有$H$ 个$featuremaps$，$W^{(1)}\in R^{H\times F}$ 为隐藏层到输出层的参数矩阵，是模型需要进行学习的。卷积结果为$Z\in R^{N\times F}$ ，F可理解为类别个数。

$$softmax(x_i)=\frac{1}{Z^{\prime }}exp(x_i),Z^{\prime }=\sum _{i}exp(x_i)$$

上述公式中是以row-wise进行softmax，$exp(x_i)$可理解为属于某个类别的logits，$Z^{\prime }$ 可理解为属于所有类别的logits。则模型的损失函数可表示为如下：

$$L=-\sum _{l\in y_L}\sum _{f=1}^F{Y}_{lf}ln{Z}_{lf}$$

上式其实就是多分类上的cross entropy loss，中 $y_L$ 为带标签的节点数量。注意第二项是在$F$ 上计算。

通过上面的推导分析，我们可以得到本论文图卷积的数学公式如下：

$$H^{(l+1)}=f(H^{(l)},A)=\sigma (\hat{A}{H}^{(l)}{W}^{(l)})$$
$$=\sigma ({\stackrel{\sim }{D}}^{-\frac{1}{2}}\stackrel{\sim }{A}{\stackrel{\sim }{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)})$$

上式中$l$ 表示卷积的隐藏层个数（叠加层数，可聚合节点本身与其$l-hops$ 的节点特征，可理解卷积感受野），$H^{(l)}$ 表示第$l$ 层的隐藏层输出，刚开始$H^{(0)}=X$，$W$ 表示模型需要学习的参数矩阵。注意在叠加多层时，$\hat{A}$ 是不变的。

单从这个公式来看，本论文所提的图上的卷积方式其实很简单的。

实验

数据集：

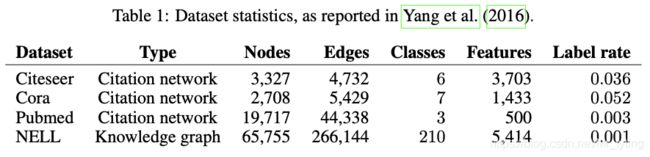
论文中用到了上述四个数据集，上表中展示了每个数据集的节点数量、边的数量、类别数、特征维度、带标签节点占比。

以Citation network（Citeseer,Cora,Pubmed）举例，该网络是大量文档组成，以文档为节点，以是否有"引用“来连边。其中每个节点的原始输入特征有词袋特征来定义获得，每个节点都有唯一所属的类别（class label)。由此构成了一张图。

实验的一些参数等设置，这里就不详叙述了。

实验结果：

上图的实验中，评价指标为节点分类的ACC，加粗的GCN(this paper) 为论文中的所提的有两层叠加的图卷积网络，GCN(rand，splits) 与GCN(this paper) 网络结构一样，只不过数据集划分上不一样而已。由上图可以看出，本论文提出的GCN网络分类效果最好。

除此之外，论文中还和以往的一些GCN网络进行了对比实验：

显然也是本论文中所提的带有Renormalization trick的GCN效果最好。

核心代码分析

抛开一系列的数学推导不管，其实本论文所提的图卷积方法可用数学公式表示如下：
$$H^{(l+1)}=\sigma ({\stackrel{\sim }{D}}^{-\frac{1}{2}}\stackrel{\sim }{A}{\stackrel{\sim }{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)})$$

初始时：$H^{(0)}=X$，而${\stackrel{\sim }{D}}^{-\frac{1}{2}}\stackrel{\sim }{A}{\stackrel{\sim }{D}}^{-\frac{1}{2}}$ 始终是不变的，可以提前计算好。因此代码实现起来其实非常简单了。

代码参考的是pygcn

开源代码中使用的数据集是Cora dataset，关于文档引用的数据集，文档定义为图中的节点，文档间是否有引用关系定义为边。由词袋特征作为节点初始特征，任务是对节点进行分类。

pygcn/data/cora/ 下有两个文本文件

• cora.cites
  每行格式如： ID of cited paper \t ID of citing paper

• cora.content
  每行格式如：paper_id word_attributes class_label

加载上述两个文件，进行构图，得到归一化后的邻接矩阵、提取节点特征、label等

def load_data(path="../data/cora/", dataset="cora"):
    """Load citation network dataset (cora only for now)"""
    print('Loading {} dataset...'.format(dataset))

    idx_features_labels = np.genfromtxt("{}{}.content".format(path, dataset),
                                        dtype=np.dtype(str))
    features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32)
    labels = encode_onehot(idx_features_labels[:, -1])

    # build graph
    idx = np.array(idx_features_labels[:, 0], dtype=np.int32)
    
    ## 获得每个paper_id在cora.content中所在的行数
    idx_map = {
     j: i for i, j in enumerate(idx)} 
    edges_unordered = np.genfromtxt("{}{}.cites".format(path, dataset),
                                    dtype=np.int32)
                                    
	## 将有连接的一对节点(paper_id在cora.content的行数）作为一行，生成一个np.array
    edges = np.array(list(map(idx_map.get, edges_unordered.flatten())),
                     dtype=np.int32).reshape(edges_unordered.shape)
    
    ## 邻接矩阵A，有边为1，反之为0
    adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),
                        shape=(labels.shape[0], labels.shape[0]),
                        dtype=np.float32)

    # 将有向边变成对称的无向边
    adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)
	
	## 归一化
    features = normalize(features)
    adj = normalize(adj + sp.eye(adj.shape[0]))

    idx_train = range(140)
    idx_val = range(200, 500)
    idx_test = range(500, 1500)

    features = torch.FloatTensor(np.array(features.todense()))
    labels = torch.LongTensor(np.where(labels)[1])
    adj = sparse_mx_to_torch_sparse_tensor(adj)

    idx_train = torch.LongTensor(idx_train)
    idx_val = torch.LongTensor(idx_val)
    idx_test = torch.LongTensor(idx_test)

    return adj, features, labels, idx_train, idx_val, idx_test

def normalize(mx):
    """Row-normalize sparse matrix"""
    rowsum = np.array(mx.sum(1))
    r_inv = np.power(rowsum, -1).flatten()
    r_inv[np.isinf(r_inv)] = 0.
    r_mat_inv = sp.diags(r_inv)
    mx = r_mat_inv.dot(mx)
    return mx

显然上述的邻居矩阵的归一化为这种形式：${\stackrel{\sim }{D}}^{-1}\stackrel{\sim }{A}$，而非${\stackrel{\sim }{D}}^{-\frac{1}{2}}\stackrel{\sim }{A}{\stackrel{\sim }{D}}^{-\frac{1}{2}}$。矩阵的归一化有多种，在上面的实验分析部分也做了不同归一化的对比。因此在实际实验中，可进行尝试，选择效果较好的一种。

class GCN(nn.Module):
    def __init__(self, nfeat, nhid, nclass, dropout):
        super(GCN, self).__init__()

        self.gc1 = GraphConvolution(nfeat, nhid)
        self.gc2 = GraphConvolution(nhid, nclass)
        self.dropout = dropout

    def forward(self, x, adj):
        x = F.relu(self.gc1(x, adj))
        x = F.dropout(x, self.dropout, training=self.training)
        x = self.gc2(x, adj)
        return F.log_softmax(x, dim=1)

上述的GCN代码就很简单的，就是叠加了两层卷积的网络，在实际训练时，网络的输入是 $X$ 和归一化后的邻接矩阵$adj$，$X$ 随着每一层的叠加在变化，而$adj$ 是固定不变的。具体可再看这个卷积是怎么做的，代码如下：

class GraphConvolution(Module):
    """
    Simple GCN layer, similar to https://arxiv.org/abs/1609.02907
    """

    def __init__(self, in_features, out_features, bias=True):
        super(GraphConvolution, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.weight = Parameter(torch.FloatTensor(in_features, out_features))
        if bias:
            self.bias = Parameter(torch.FloatTensor(out_features))
        else:
            self.register_parameter('bias', None)
        self.reset_parameters()

    def reset_parameters(self):
        stdv = 1. / math.sqrt(self.weight.size(1))
        self.weight.data.uniform_(-stdv, stdv)
        if self.bias is not None:
            self.bias.data.uniform_(-stdv, stdv)

    def forward(self, input, adj):
        support = torch.mm(input, self.weight)
        output = torch.spmm(adj, support)
        if self.bias is not None:
            return output + self.bias
        else:
            return output

    def __repr__(self):
        return self.__class__.__name__ + ' (' \
               + str(self.in_features) + ' -> ' \
               + str(self.out_features) + ')'

上面代码主要看forward部分即可，显然实现的就是 $XW\hat{A}$ 操作而已。

模型训练和测试

def train(epoch):
    t = time.time()
    model.train()
    optimizer.zero_grad()
    output = model(features, adj)
    loss_train = F.nll_loss(output[idx_train], labels[idx_train])
    acc_train = accuracy(output[idx_train], labels[idx_train])
    loss_train.backward()
    optimizer.step()

    if not args.fastmode:
        # Evaluate validation set performance separately,
        # deactivates dropout during validation run.
        model.eval()
        output = model(features, adj)

    loss_val = F.nll_loss(output[idx_val], labels[idx_val])
    acc_val = accuracy(output[idx_val], labels[idx_val])
    print('Epoch: {:04d}'.format(epoch+1),
          'loss_train: {:.4f}'.format(loss_train.item()),
          'acc_train: {:.4f}'.format(acc_train.item()),
          'loss_val: {:.4f}'.format(loss_val.item()),
          'acc_val: {:.4f}'.format(acc_val.item()),
          'time: {:.4f}s'.format(time.time() - t))


def test():
    model.eval()
    output = model(features, adj) ### 注意 test阶段的 feature,adj与训练阶段完全一样
    # 也就是网络图完全一样，并没有发生任何改变，只是用来预测的节点和训练节点不一样
    loss_test = F.nll_loss(output[idx_test], labels[idx_test])
    acc_test = accuracy(output[idx_test], labels[idx_test])
    print("Test set results:",
          "loss= {:.4f}".format(loss_test.item()),
          "accuracy= {:.4f}".format(acc_test.item()))


# Train model
t_total = time.time()
for epoch in range(args.epochs):
    train(epoch)
print("Optimization Finished!")
print("Total time elapsed: {:.4f}s".format(time.time() - t_total))

# Testing
test()

注意：注意 test阶段的 feature,adj与训练阶段完全一样，也就是两阶段所用的graph完全一样，只是用来预测的节点和训练节点不一样； 并不是在一张图上训练，在另外一张图上预测，，所以说是半监督。

个人总结

• 本论文模型上的创新点主要有亮点：一是 提出了在图上的快速卷积的模型（K=1)，第二是提出了renormalization_trick
• 在限制K=1时，大大限制了模型参数数量，同时可实现多层的叠加，当叠加l层时，可聚合节点自身及其l-hops的节点特征。叠加层数越大，卷积感受野越大。
• 抛去繁杂的数学公式推导，感性理解本论文所提出的快速卷积，其实非常简单：
  $$H^{(l+1)}=\sigma ({\stackrel{\sim }{D}}^{-\frac{1}{2}}\stackrel{\sim }{A}{\stackrel{\sim }{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)})$$
  

参考资料

• https://arxiv.org/pdf/1609.02907.pdf
• https://github.com/tkipf/pygcn