2021SWPU-ACM 预选赛题解 Tutorial of SWPU Pre-teammate Contest ( 2021 )

Tutorial of SWPU Pre-teammate Contest ( 2021 )

敬请关注新生赛！SWPU-ACM官方群：815161393 !

作者 ：2020级 Tekola. AND 2020级 Moon.

赛题依然开放，点击 SWPU Pre-teammate Contest ( 2021 ) 可进行答题。

A. Hello ACM !

灵感来自 Luogu P1000 超级玛丽游戏

• 最早的目标是希望全部人都通过本题，结果还是有读错题目的同学 qwq。
• 对于一些脚本语言，本题可以过得很轻松，如 PHP, Python, Bash 等。
• 对于 C++， 这里给出两个技巧。
  • 首先是 Visual Studio Code 中的快捷键 Crtl + Shift + Alt 多行 Insert
  • 其次是使用 \ 以连缀多行

B. orange

• 阅读到最后，发现是 “可橙”， 用拼音打出来就是 “kecheng”

C. 老王的礼物

题意：将给定字符串中的 ‘4’ 改成 ‘6’, ‘7’ 改成 ‘8’，输出修改次数以及最终的字符串。

• 直接模拟即可。

#include 

char str[7 + 20000];
int main() {
     
    int n, cnt = 0;
    scanf("%d\n%[^\n]", &n, str + 1);
    for (int i = 1; i <= n; ++i) {
     
        cnt += str[i] == '4' || str[i] == '7';
        str[i] = str[i] == '4' ? '6' : str[i] == '7' ? '8' : str[i];
    }
    printf("%d\n%s", cnt, str + 1);
    return 0;
}

• 其他语言 (包括C++) 容易实现，下面给出 Python 的解答：

input()
s = input().strip()
print( s.count('4') + s.count('7') )
print( s.replace('4', '6').replace('7', '8') )

D. Team Fight

• 英文题面。
• 容易得出结论：当 Orange 的战斗力小于任意一个敌人时就会输掉比赛。
• 要开 long long，或者使用字符串处理本题。很多同学没有注意到 Note that numbers may exceed the max value of ‘int’ 。
• 比较 Corner 的是测试数据中包含负数，所以有的同学写的高精也挂了。
• 另外，本题由于输出的是中文，有可能会因为本机编码问题输不出中文然后一直调不对，我们会避免你之后出现这样的情况。

#include 
int main () {
     
    long long orange, enemy;
    int flag = 1;
    
    scanf("%lld", &orange);
    for (int i = 0; flag && i < 7; ++i)
        scanf("%lld", &enemy), flag = enemy < orange;
    
    puts( flag ? "恭喜橘子云顶吃鸡" : "猪鼻吧，怎么这么菜啊");
    return 0;
}

E. K2检测

• 这个题直接从高考卷上抄的，甚至第一组的数据都是一样的 (手动狗头)。
• 但是这个题的输描述写反了，不过样例以及测试数据都是对的。当时我不在团队盯榜，所以没及时解决，难为各位了。
• 比较 trick 的一点是输出 '%' 的时候放弃 printf("%%..") 而直接选用 puts("%..")，这边就直接 ""%s" 好了。

#include 

int main() {
     
    double a, b, c, d;
    scanf("%lf%lf%lf%lf", &a, &b, &c, &d);
    double n = a + b + c + d,
        temp = (a + b) * (c + d) * (a + c) * (b + d),
        ans = (n * ((a * d) - (b * c)) * ((a * d) - (b * c)) / temp);
    
    printf("%.2f\n%s", ans, ans > 6.635 ? "99% sure" : "Not 99% sure");
    return 0;
}

F. 一次旅行

USACO training 原题

题意： 有一些人相互送了礼物，求最终的净收入
分析： 建立 结构体，处理好输入即可，判断有没有送礼人、有没有送礼。之后需要两次循环分别计算支出和收入。

• 下面是出题人提供的 STD

#include 
#include 

#define N 25

int n;
struct people {
     
	int meoney;
	char name[N];
} peop[N];

void change(char s[], int x) {
     
	for (int i = 1; i <= n; i++) {
     
		if (!strcmp(peop[i].name, s)) {
     
			peop[i].meoney += x;
			return;
		}
	}
}

int main() {
     
	scanf("%d", &n);

	for (int i = 1; i <= n; i++)
		scanf("%s", peop[i].name);

	char s[N];
	int how, hw;
	while (scanf("%s%d%d", s, &hw, &how) == 3) {
     
		if (how == 0) continue;
		int add = hw / how;
		change(s, -(add * how));
		for (int i = 1; i <= how; i++) {
     
			scanf("%s", s);
			change(s, add);
		}
	}

	for (int i = 1; i <= n; i++)
		printf("%s %d\n", peop[i].name, peop[i].meoney);
	return 0;
}

G. 不是吧？涛涛又在团队摸鱼！(1)

• 我们要想将每一个拉杆都以最大价值利用的话，一个对应着三个灯即可。最小价值利用的话把所有打开都打开即可。

#include 
int main() {
     
    int t, n;
    scanf("%d", &t);
    while ( t -- ) {
     
        scanf("%d", &n);
        printf("%d$%d\n", ( n + 2 ) / 3, n);
    }
    return 0;
}

H.不是吧？涛涛又在团队摸鱼！(2)

• 本场思维天花板。
• 不同于刚才的那道题，现在拉杆不能影响相邻的方块了。并且本题中给了非常多的数据，表示按下的顺序。我们首先思考顺序重不重要。从一轮一轮扫过去这样想当然复杂，我们不妨考虑每一盏灯的情况，我们发现从最初的熄灭到最终满足题意的亮灯，这个灯被按了 奇数次。因此，与顺序无关。
• 所以我们只需要思考，最终亮着的灯有什么共同特点。被按了奇数次，而实际上只有灯编号的因子才可能按到这盏灯。容易想到，因子有奇数个的数是完全平方数。
• 因此题目改造为，求 $n$ 以内的完全平方数个数几何。而这个数显然就是 $\lfloor \sqrt{n}\rfloor$，本题阐述完毕。

#include 
#include 
int main() {
     
    int t, n;
    scanf("%d%d", &n, &t);
    while ( t-- )
        printf("%d\n", (int)sqrt(n));
    return 0;
}

I. 伊甸园

Luogu P3150 pb的游戏（1）

• 首先劝退的是庞大的读入，如果是 C++ 选手，不开挂 ios::sync_with_stdio(false), cin.tie(nullptr) 会被卡掉输入。其他语言的输入挂在此不做赘述。
• 下面开始思考 Moon 的这道题目。题干是一个标准的对称博弈论，即游戏结果仅与选手的策略有关，换句话说，这局游戏的结果一开始就确定了。当时我们考虑过，出博弈合不合适，看到别的团队也在介绍博弈，所以我们就放心地出啦 ~
• 这种问题一般是从必胜必败点开始推导的。我们注意到，「分」的最小操作数目是 $2$，如果 选手 $\mathrm{A}$ 遇到 $n=2$， 那么他唯一能做的就是赢下本场游戏；反之，如果为 $1$，选手必败。因此我们考虑将对手逼至无路可走，每次我只分出 $1$ 来，那么对家唯一能做的就是分剩下的那一堆。可见，能分出 $1$ 的次数决定了本局的胜负。而这实际上就是对于 $n$ 进行奇偶性判定，可以说是有手就行。

#include 
int main() {
     
    int t;
    long long i;
    scanf("%d", &t);
    while (t--) {
     
        scanf("%lld", &i);
        puts( i & 1 ? "Moon,I'm coming" : "Sorry,Moon");
    }
    return 0;
}

J. 简单的数学题

• 要素比较多，包括「素数判定」,「分解约数」,「输出格式」和「降序排序」，实际上本题是为学习过四者的同学准备的。

• 学习过这四样之后，直接模拟即可，况且本身也是网络赛，现场学也来得及 (不是)。

• 为了敲得快一点，我直接使用的 C++ ：

#include 
using namespace std;
multiset<int> ans;
int t, cnt, it;
bool isP(int n) {
         
    if (n <= 1) return false;    
    for (int i = 2; i <= sqrt(n); ++i) 
        if (n % i == 0) return false;    
     return true;
}
int main () {
     
    while (cin >> it) {
      
        t = it, cnt = 0;
        for (int i = 2; i <= it; ++i) {
      
            while ( t % i == 0) cnt ++, t /= i; 
            if (!t) break;        
        }        
        if (isP(cnt)) ans.insert(it);
    }    
    cnt = 1;
    if (!ans.size()) cout << '\n';    
    for (auto it = ans.rbegin(); it != ans.rend(); ++it) {
     
        cout << *it << ",\n"[cnt++ == ans.size()];    
    }    
    cout << (isP(ans.size()) ? "Yes" : "No" ) << '\n';    
    return 0;
}

• C 的版本也可以写一个，主要是用来告诉各位 sort 不只是 C++ 才有：

#include 
#include 
#include 

int top, stk[10001];
int n, q, t, cnt;

int isP(int n) {
     
    if (n <= 1) return 0;
    for (int i = 2; i <= sqrt(n); ++i) if (n % i == 0) return 0;
    return 1;
}

int cmp(const void * a, const void * b) {
      
    return *(int *)b - *(int *)a; 
}

int main() {
     
    while (~scanf("%d", &n)) {
     
        t = n, cnt = 0;
        for (int i = 2; i <= n; ++i) {
     
            while ( t % i == 0) cnt ++, t /= i;
            if (!t) break;
        }
        if (isP(cnt)) stk[++ top] = n;
    }
    if ( !top ) puts("");
    
    // 直接使用函数的名当做函数的参数，这个参数被称作函数指针
    qsort(stk + 1, top, sizeof(int), cmp);
    
    for (int i = 1; i <= top; ++i)
        printf("%d%c", stk[i], ",\n"[top == i]);
    
    puts( isP(top) ? "Yes" : "No");
    
    return 0;
}

K.涛涛们的烦恼（原2021icpc网络赛第一场K题）

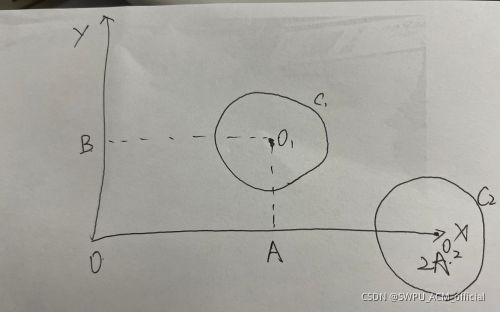
• 这是一道数学题，我们可以把它化简为求O到$C_1$内一点加上这一点到$O_2$的最小值减去R。

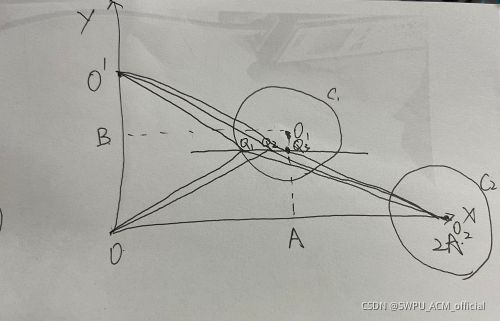
• 取任意一条过$C_1$的直线l，先找到当点Q在l上时，OQ+Q$O_2$的最小值，先取l上任意两点$Q_1$，$Q_2$，将O与$Q_1$和$Q_1$与$O_2$和O与$Q_2$和$Q_2$与$O_2$连起来。

• 我们可以很明显的想到利用对称性来解决这个问题，做O点关于l的对称点，连起来即为最小距离。
  

• $Q_3$即为所求。易证$Q_3$在O$O_2$的中垂线上。当l在接近x轴的时候显然比远离x的最优，所以显然，$C_1$的最底点即为题目所求。

• 但是这个只考虑了一种情况，还有一种情况，就是$C_1$与x轴有交点时，直接去$O_2$点显然更近。

• 其实还有一种$C_1$与$C_2$相交的情况，但是题目的数据规避了这个问题，这种情况可以忽略。这道题还有一个小小的点，就是因为Moon没有过4级（实际上是涛涛的锅）需要特判一下是第几只涛涛。下附代码：

#include 
char* d[11]={
     "th","st","nd","rd","th","th","th","th","th","th"};
int main() {
     
	int T;
	scanf("%d", &T);
	for(int t=1;t<=T;t++) {
     
		double a,b,c;
		scanf("%lf%lf%lf", &a, &b, &c);
		double ans=0;
		if(b<=c)
			ans=2*a-c;
		else
			ans=2*sqrt(a*a+(b-c)*(b-c))-c;
		printf("The shortest path of the %d%s Tekola is %.2f.\n", t, d[t % 10], ans);
	}
	return 0;
}

总结

本场比赛题目整体难度均衡，对新生极其友好。赛中有以为选手一血了 $6$ 道题，并且最终有两位大一选手 AK ！

也算是圆满了吧 ~