拓端tecdat|在r语言中使用GAM(广义相加模型)进行电力负荷时间序列分析
原文链接:http://tecdat.cn/?p=9024
原文出处:拓端数据部落公众号
用GAM进行建模时间序列
我已经准备了一个文件,其中包含四个用电时间序列来进行分析。数据操作将由data.table程序包完成。
将提及的智能电表数据读到data.table。
DT <- as.data.table(read_feather("DT_4_ind"))使用GAM回归模型。将工作日的字符转换为整数,并使用recode包中的函数重新编码工作日:1.星期一,…,7星期日。
DT[, week_num := as.integer(car::recode(week,
"'Monday'='1';'Tuesday'='2';'Wednesday'='3';'Thursday'='4';
'Friday'='5';'Saturday'='6';'Sunday'='7'"))]将信息存储在日期变量中,以简化工作。
n_type <- unique(DT[, type])
n_date <- unique(DT[, date])
n_weekdays <- unique(DT[, week])
period <- 48让我们看一下用电量的一些数据并对其进行分析。
data_r <- DT[(type == n_type[1] & date %in% n_date[57:70])]
ggplot(data_r, aes(date_time, value)) +
geom_line() +
theme(panel.border = element_blank(),
panel.background = element_blank(),
panel.grid.minor = element_line(colour = "grey90"),
panel.grid.major = element_line(colour = "grey90"),
panel.grid.major.x = element_line(colour = "grey90"),
axis.text = element_text(size = 10),
axis.title = element_text(size = 12, face = "bold")) +
labs(x = "Date", y = "Load (kW)")在绘制的时间序列中可以看到两个主要的季节性:每日和每周。我们在一天中有48个测量值,在一周中有7天,因此这将是我们用来对因变量–电力负荷进行建模的自变量。
训练我们的第一个GAM。通过平滑函数s对自变量建模,对于每日季节性,使用三次样条回归,对于每周季节性,使用P样条。
gam_1 <- gam(Load ~ s(Daily, bs = "cr", k = period) +
s(Weekly, bs = "ps", k = 7),
data = matrix_gam,
family = gaussian)首先是可视化。
layout(matrix(1:2, nrow = 1))
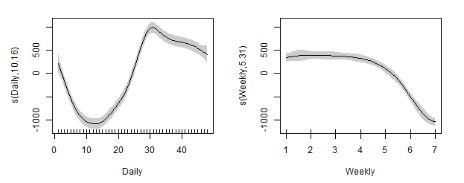
plot(gam_1, shade = TRUE)我们在这里可以看到变量对电力负荷的影响。在左图中,白天的负载峰值约为下午3点。在右边的图中,我们可以看到在周末负载量减少了。
让我们使用summary函数对第一个模型进行诊断。
##
## Family: gaussian
## Link function: identity
##
## Formula:
## Load ~ s(Daily, bs = "cr", k = period) + s(Weekly, bs = "ps",
## k = 7)
##
## Parametric coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2731.67 18.88 144.7 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Approximate significance of smooth terms:
## edf Ref.df F p-value
## s(Daily) 10.159 12.688 119.8 <2e-16 ***
## s(Weekly) 5.311 5.758 130.3 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## R-sq.(adj) = 0.772 Deviance explained = 77.7%
## GCV = 2.4554e+05 Scale est. = 2.3953e+05 n = 672EDF:估计的自由度–可以像对给定变量进行平滑处理那样来解释(较高的EDF值表示更复杂的样条曲线)。P值:给定变量对因变量的统计显着性,通过F检验进行检验(越低越好)。调整后的R平方(越高越好)。我们可以看到R-sq.(adj)值有点低。
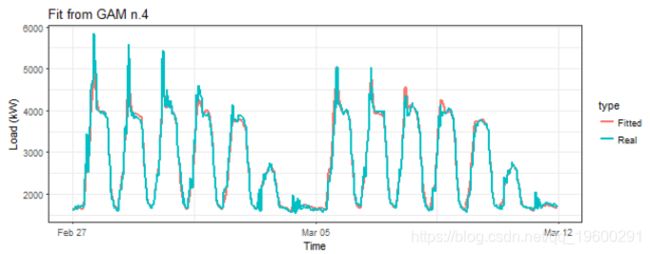
让我们绘制拟合值:
我们需要将两个自变量的交互作用包括到模型中。
第一种交互类型对两个变量都使用了一个平滑函数。
gam_2 <- gam(Load ~ s(Daily, Weekly),
summary(gam_2)$r.sq## [1] 0.9352108R方值表明结果要好得多。
summary(gam_2)$s.table## edf Ref.df F p-value
## s(Daily,Weekly) 28.7008 28.99423 334.4754 0似乎也很好,p值为0,这意味着自变量很重要。拟合值图:
现在,让我们尝试上述张量积交互。这可以通过function完成te,也可以定义基本函数。
## [1] 0.9268452与以前的模型相似gam_2。
summary(gam_3)$s.table## edf Ref.df F p-value
## te(Daily,Weekly) 23.65709 23.98741 354.5856 0非常相似的结果。让我们看一下拟合值:
与gam_2模型相比,只有一点点差异,看起来te拟合更好。
## [1] 0.9727604summary(gam_4)$sp.criterion## GCV.Cp
## 34839.46summary(gam_4)$s.table## edf Ref.df F p-value
## te(Daily,Weekly) 119.4117 149.6528 160.2065 0我们可以在这里看到R方略有上升。
让我们绘制拟合值:
这似乎比gam_3模型好得多。
## [1] 0.965618summary(gam_4_fx)$s.table## edf Ref.df F p-value
## te(Daily,Weekly) 335 335 57.25389 5.289648e-199我们可以看到R平方比模型gam_4低,这是因为我们过度拟合了模型。证明GCV程序(lambda和EDF的估计)工作正常。
因此,让我们在案例(模型)中尝试ti方法。
## [1] 0.9717469summary(gam_5)$sp.criterion## GCV.Cp
## 35772.35summary(gam_5)$s.table## edf Ref.df F p-value
## s(Daily) 22.583649 27.964970 444.19962 0
## s(Weekly) 5.914531 5.995934 1014.72482 0
## ti(Daily,Weekly) 85.310314 110.828814 41.22288 0然后使用t2。
## [1] 0.9738273summary(gam_6)$sp.criterion## GCV.Cp
## 32230.68summary(gam_6)$s.table## edf Ref.df F p-value
## t2(Daily,Weekly) 98.12005 120.2345 86.70754 0我还输出了最后三个模型的GCV得分值,这也是在一组拟合模型中选择最佳模型的良好标准。我们可以看到,对于t2相应模型gam_6,GCV值最低。
在统计中广泛使用的其他模型选择标准是AIC(Akaike信息准则)。让我们看看三个模型:
AIC(gam_4, gam_5, gam_6)## df AIC
## gam_4 121.4117 8912.611
## gam_5 115.8085 8932.746
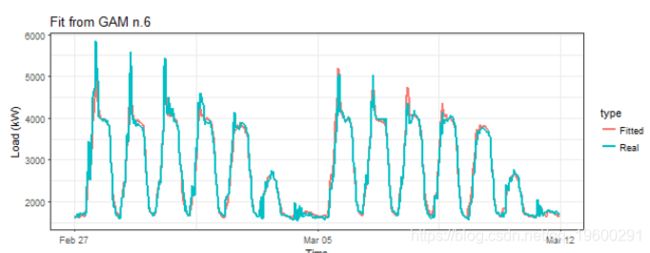
## gam_6 100.1200 8868.628最低值在gam_6模型中。让我们再次查看拟合值。
我们可以看到的模型的拟合值gam_4和gam_6非常相似。可以使用软件包的更多可视化和模型诊断功能来比较这两个模型。
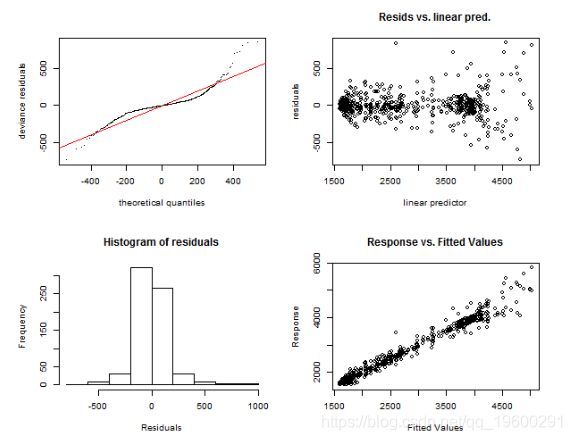
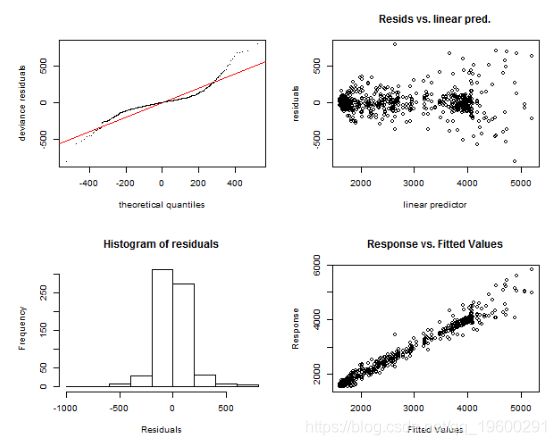
第一个是function gam.check,它绘制了四个图:残差的QQ图,线性预测变量与残差,残差的直方图以及拟合值与因变量的关系图。让我们诊断模型gam_4和gam_6。
gam.check(gam_4)##
## Method: GCV Optimizer: magic
## Smoothing parameter selection converged after 7 iterations.
## The RMS GCV score gradiant at convergence was 0.2833304 .
## The Hessian was positive definite.
## The estimated model rank was 336 (maximum possible: 336)
## Model rank = 336 / 336
##
## Basis dimension (k) checking results. Low p-value (k-index<1) may
## indicate that k is too low, especially if edf is close to k'.
##
## k' edf k-index p-value
## te(Daily,Weekly) 335.00 119.41 1.22 1gam.check(gam_6)##
## Method: GCV Optimizer: magic
## Smoothing parameter selection converged after 9 iterations.
## The RMS GCV score gradiant at convergence was 0.05208856 .
## The Hessian was positive definite.
## The estimated model rank was 336 (maximum possible: 336)
## Model rank = 336 / 336
##
## Basis dimension (k) checking results. Low p-value (k-index<1) may
## indicate that k is too low, especially if edf is close to k'.
##
## k' edf k-index p-value
## t2(Daily,Weekly) 335.00 98.12 1.18 1我们可以再次看到模型非常相似,只是在直方图中可以看到一些差异。
layout(matrix(1:2, nrow = 1))
plot(gam_4, rug = FALSE, se = FALSE, n2 = 80, main = "gam n.4 with te()")
plot(gam_6, rug = FALSE, se = FALSE, n2 = 80, main = "gam n.6 with t2()") 该模型gam_6 有更多的“波浪形”的轮廓。因此,这意味着它对因变量的拟合度更高,而平滑因子更低。
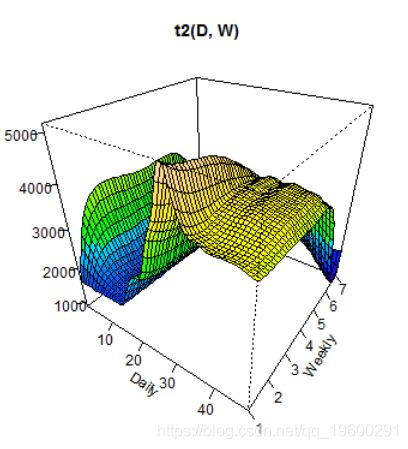
vis.gam(gam_6, n.grid = 50, theta = 35, phi = 32, zlab = "",
ticktype = "detailed", color = "topo", main = "t2(D, W)")我们可以看到最高峰值是Daily变量的值接近30(下午3点),而Weekly变量的值是1(星期一)。
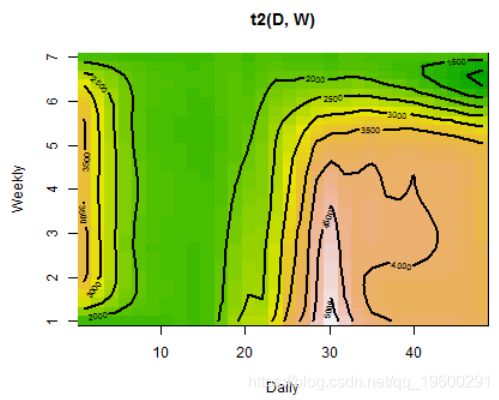
vis.gam(gam_6, main = "t2(D, W)", plot.type = "contour",
color = "terrain", contour.col = "black", lwd = 2)再次可以看到,电力负荷的最高值是星期一的下午3:00,直到星期四都非常相似,然后负荷在周末减少。
最受欢迎的见解
1.在python中使用lstm和pytorch进行时间序列预测
2.python中利用长短期记忆模型lstm进行时间序列预测分析
3.使用r语言进行时间序列(arima,指数平滑)分析
4.r语言多元copula-garch-模型时间序列预测
5.r语言copulas和金融时间序列案例
6.使用r语言随机波动模型sv处理时间序列中的随机波动
7.r语言时间序列tar阈值自回归模型
8.r语言k-shape时间序列聚类方法对股票价格时间序列聚类
9.python3用arima模型进行时间序列预测