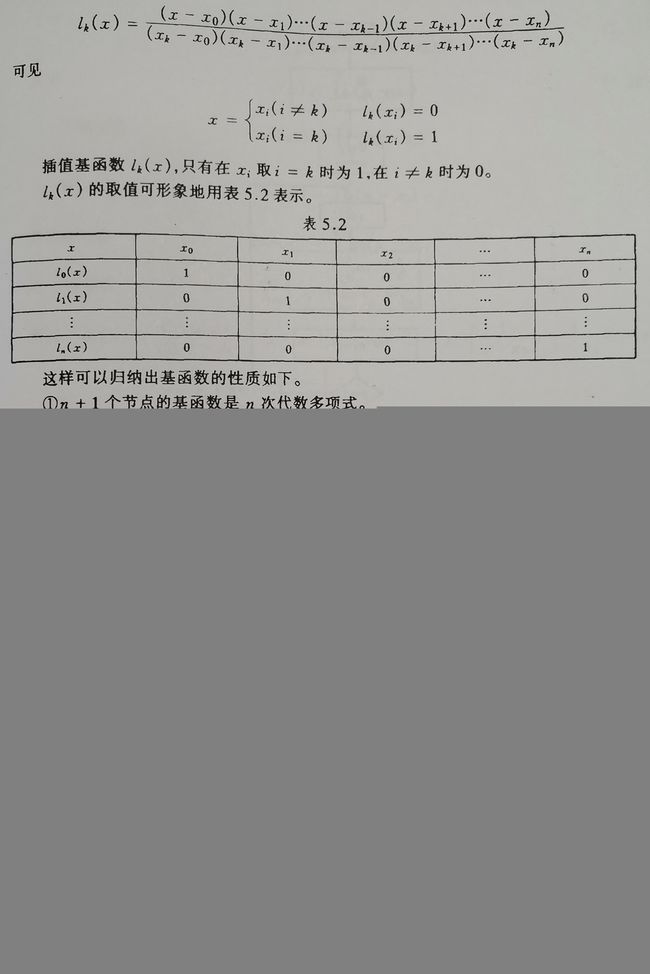
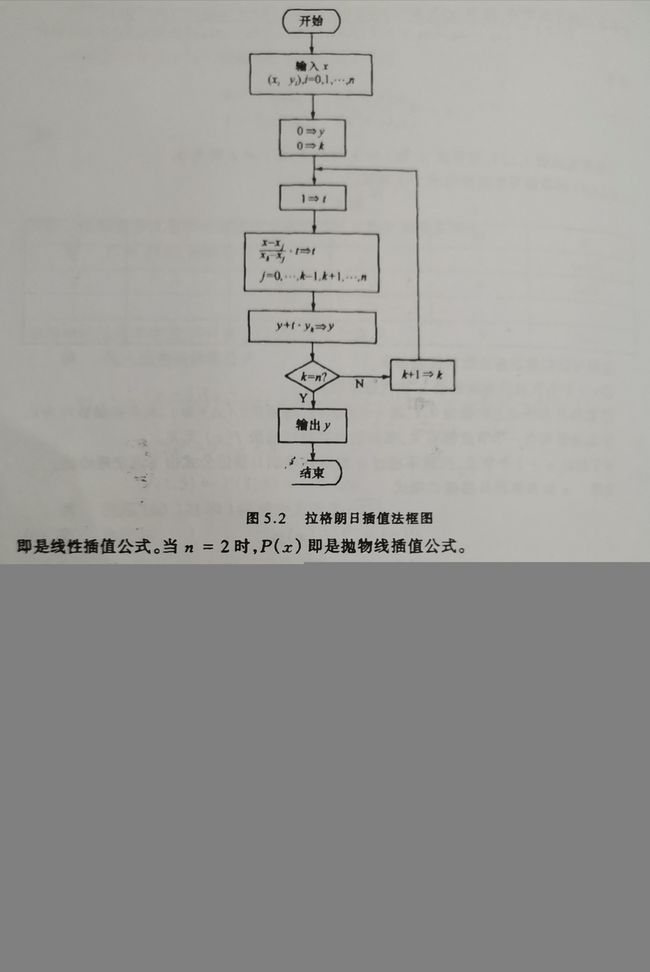
拉格朗日插值法的Python程序
线性插值和抛物线插值
#两点拉格朗日线性插值,一次插值多项式
x_list = [1, 3]
y_list = [1, 2]
#所要求的插值x的值
x = 1.5
l_0 = (x - x_list[1]) / (x_list[0] - x_list[1])
l_1 = (x - x_list[0]) / (x_list[1] - x_list[0])
P = l_0 * y_list[0] + l_1 * y_list[1]
print(P)
结果:
1.25
#两点拉格朗日线性插值,一次插值多项式
x_list = [100, 121]
y_list = [10, 11]
#所要求的插值x的值
x = 115
l_0 = (x - x_list[1]) / (x_list[0] - x_list[1])
l_1 = (x - x_list[0]) / (x_list[1] - x_list[0])
P = l_0 * y_list[0] + l_1 * y_list[1]
print(P)
结果:
10.714285714285715
#三点拉格朗日抛物线插值
x_list = [1, 3, 2]
y_list = [1, 2, -1]
#所要求的插值x的值
x = 1.5
l_0 = ((x - x_list[1]) * (x - x_list[2])) / ((x_list[0] - x_list[1]) * (x_list[0] - x_list[2]))
l_1 = ((x - x_list[0]) * (x - x_list[2])) / ((x_list[1] - x_list[0]) * (x_list[1] - x_list[2]))
l_2 = ((x - x_list[0]) * (x - x_list[1])) / ((x_list[2] - x_list[0]) * (x_list[2] - x_list[1]))
P = l_0 * y_list[0] + l_1 * y_list[1] + l_2 * y_list[2]
print(P)
结果:
-0.625
#三点拉格朗日抛物线插值
x_list = [100, 121, 144]
y_list = [10, 11, 12]
#所要求的插值x的值
x = 115
l_0 = ((x - x_list[1]) * (x - x_list[2])) / ((x_list[0] - x_list[1]) * (x_list[0] - x_list[2]))
l_1 = ((x - x_list[0]) * (x - x_list[2])) / ((x_list[1] - x_list[0]) * (x_list[1] - x_list[2]))
l_2 = ((x - x_list[0]) * (x - x_list[1])) / ((x_list[2] - x_list[0]) * (x_list[2] - x_list[1]))
P = l_0 * y_list[0] + l_1 * y_list[1] + l_2 * y_list[2]
print(P)
结果:
10.722755505364201
基函数和拉格朗日插值公式
#拉格朗日插值多项式
from sympy import *
x = Symbol('x')
x_list = [0, 1, 2]
y_list = [1, 2, 3]
l_list = []
for i in range(len(x_list)):
X, Y = 1, 1
for j in range(len(y_list)):
if i == j:
pass
else:
X = X * (x - x_list[j])
Y = Y * (x_list[i] - x_list[j])
l = expand(X / Y) #扩展代数表达式
l_list.append(l)
P = 0
for k in range(len(y_list)):
P += l_list[k] * y_list[k]
print(P)
结果:
x + 1
#拉格朗日插值多项式
from sympy import *
x = Symbol('x')
x_list = [1, 2, 3, 4]
y_list = [0, -5, -6, 3]
l_list = []
for i in range(len(x_list)):
X, Y = 1, 1
for j in range(len(y_list)):
if i == j:
pass
else:
X = X * (x - x_list[j])
Y = Y * (x_list[i] - x_list[j])
l = expand(X / Y) #扩展代数表达式
l_list.append(l)
P = 0
for k in range(len(y_list)):
P += l_list[k] * y_list[k]
print(P)
结果:
x**3 - 4*x**2 + 3
迭代插值
#拉格朗日插值多项式
from sympy import *
x = 50
x_list = [45, 60, 30, 90, 0]
def f(a):
f = sin(a/180*pi)
return f.evalf()
n = len(x_list)
P = 0
for i in range(n):
X, Y = 1, 1
for j in range(n):
if i == j:
pass
else:
X = X * (x - x_list[j])
Y = Y * (x_list[i] - x_list[j])
P += X/Y*f(x_list[i])
print(P)
结果:
0.766025943265555
#拉格朗日插值多项式
from sympy import *
x = 1/2
x_list = [-2, -1, 0, 1, 2]
def f(a):
f = 3**a
return f
n = len(x_list)
P = 0
for i in range(n):
X, Y = 1, 1
for j in range(n):
if i == j:
pass
else:
X = X * (x - x_list[j])
Y = Y * (x_list[i] - x_list[j])
P += X/Y*f(x_list[i])
print(P)
结果:
1.7083333333333335