皮尔森相关系数与方差膨胀因子介绍及关系 附python代码

1.皮尔森相关系数

参考文档：https://www.zhihu.com/question/20852004

2.方差膨胀因子

图片来源：http://sofasofa.io/forum_main_post.php?postid=1000484

R²称为可决系数(Coefficient of determination)。
复相关系数Ri等于：（来源百度百科）

3.二者区别

皮尔森相关系数：

复相关系数R：
图片来源：https://zhuanlan.zhihu.com/p/37605060

皮尔森相关系数中的Y是一个单变量
而复相关系数R中的y^则是除了xi之外其余x的拟合 y(也就是xi) 的值

在计算结果上：

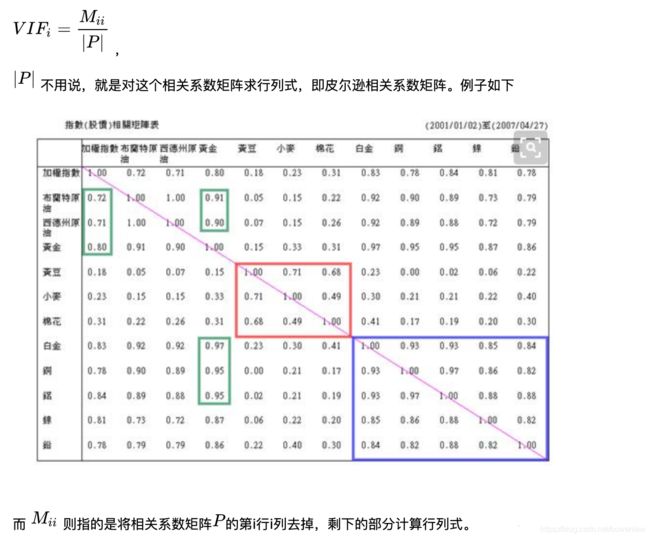
图片来源：
https://www.cnblogs.com/wqbin/p/11109650.html
https://www.zhihu.com/question/270451437

总结：

方差膨胀因子多用于金融领域，判断单变量和多变量的相关关系，进而通过逐步回归的方式，在特征尽可能少的情况下，得到最优模型。

皮尔森相关系数多用于机器学习领域，判断单变量和单变量之间的关系，消除特征间相关性。

相关教材参考连接：点击跳转1 | 点击跳转2

附python代码：

1.相关系数：

import pandas as pd

tt = pd.DataFrame({
     "A":[1,2,3,4,5,6,7],"B":[4,5,9,8,7,6,0],"C":[11,34,55,77,88,99,44],"D":[34,56,87,47,5,9,13]})

tt.head()

 	A 	B 	C 	D
0 	1 	4 	11 	34
1 	2 	5 	34 	56
2 	3 	9 	55 	87
3 	4 	8 	77 	47
4 	5 	7 	88 	5


pearson_value = tt.corr()
# pearson_value.to_csv("./data/pearson_value.csv")
pearson_value.head()

结果：

	A 	B 	C 	D
A 	1.000000 	-0.309426 	0.642899 	-0.617804
B 	-0.309426 	1.000000 	0.463917 	0.495642
C 	0.642899 	0.463917 	1.000000 	-0.363149
D 	-0.617804 	0.495642 	-0.363149 	1.000000

其中tt为df，且必须全为数值型，并且不能有空值。

2.VIF计算

import numpy as np
import pandas as pd
from statsmodels.stats.outliers_influence import variance_inflation_factor

vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(tt.values, i) for i in range(tt.shape[1])]
vif["features"] = tt.columns
vif.head()

结果：
 	VIF Factor 	features
0 	29.076246 	A
1 	66.955265 	B
2 	96.312763 	C
3 	15.317779 	D

3.利用方法删除相关性过高特征

代码来源：点击跳转

• pearson相关性：

利用相关系数删除相关性过高的变量（df中变量先得按IV值从大到小排序）

# cutoff 为（-1.1） 按顺序删除相关性高于cutoff的特征
import numpy as np
import pandas as pd

def get_var_no_colinear(cutoff, df):
    corr_high = df.corr().applymap(lambda x: np.nan if x>cutoff else x).isnull()
    col_all = corr_high.columns.tolist()
    del_col = []
    i = 0
    while i < len(col_all)-1:
        ex_index = corr_high.iloc[:,i][i+1:].index[np.where(corr_high.iloc[:,i][i+1:])].tolist()
        for var in ex_index:
            col_all.remove(var)
        corr_high = corr_high.loc[col_all, col_all]
        i += 1
    return col_all

get_var_no_colinear(0.5,tt)

#输出为可用特征列
结果：
['A', 'B', 'D'] 

• VIF

一般VIF高于10的特征需要删除

import numpy as np
import pandas as pd
from statsmodels.stats.outliers_influence import variance_inflation_factor
## 每轮循环中计算各个变量的VIF，并删除VIF>threshold 的变量
def vif(x, thres=10.0):
    X_m = np.matrix(x)
    VIF_list = [variance_inflation_factor(X_m, i) for i in range(X_m.shape[1])]
    maxvif=pd.DataFrame(VIF_list,index=x.columns,columns=["vif"])
    col_save=list(maxvif[maxvif.vif<=float(thres)].index)
    col_delete=list(maxvif[maxvif.vif>float(thres)].index)
    print(maxvif)
    print('删除特征:', col_delete)
    return x[col_save]
vif(tt)

结果：

"删除特征: ['A', 'B', 'C', 'D']"

说明：全被删除，说明我们造的数据不好，/[哭笑不得]




def vif2(x, thres=10.0):
    X_m = np.matrix(x)
    VIF_list = [variance_inflation_factor(X_m, i) for i in range(X_m.shape[1])]
    maxvif=pd.DataFrame(VIF_list,index=x.columns,columns=["VIF"])
#     print(maxvif[:10])
    col_save=list(maxvif[maxvif.VIF<=float(thres)].index)
    col_delete=list(maxvif[maxvif.VIF>float(thres)].index)
#     print(maxvif)
    print('删除特征:', col_delete)
    return maxvif



vif_feature = tttfeature[ss]

vif_data = vif2(vif_feature)

vif_data.sort_values(by='VIF', ascending=False, inplace=True)

vif_data.to_csv("./data/0521-step-3-vif_value.csv")

vif_data.head()

结果：

 	               VIF
XXX数 	    3.871011
XXX息 	3.509363
XXXXX 	3.354639
XXXXXA 	3.287080
XXXXXV 	3.151003