剑指offer_二叉树的打印合集(C++_上下打印.换行打印.之字打印_bfs+栈与队列+用表格模拟栈队列操作)

换行打印链接
之字打印链接

1.从上到下打印二叉树思路（队列）

如上图的二叉树从上到下打印为：
1 2 3 4 5

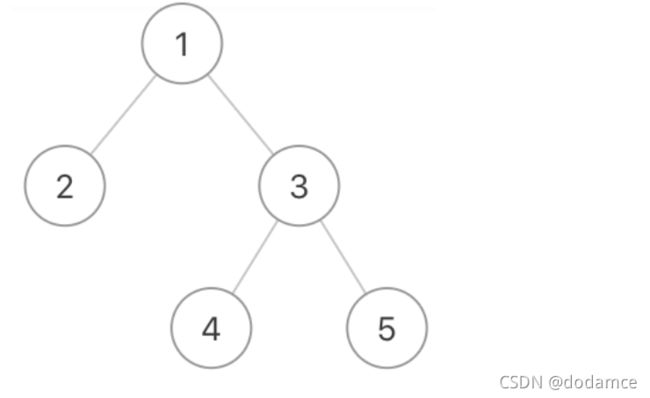
如果这个二叉树不为空的话，我们要先打印节点1，再通过节点1的指针来打印2和3，即扫描第二层，最后通过节点3打印4，5。这实际上为二叉树的广度优先遍历（dfs）

我们要将节点1所指向的2和3存起来，又因为最后打印要从左向右，所以我们选择队列这种先进先出的数据结构。队列存放的是树节点的指针，其类型为TreeNode*

打印完这个节点后将队列中的这个节点指向的左右子树入队，再把这个节点指针出队。

注意一定要在有左右子树的时候在进队。

操作	队列中的值
打印1	节点2，节点3
打印2	节点3
打印3	节点4，节点5
打印4	节点5
打印5	空

C/C++代码

struct TreeNode
{
     
	int m_nValue;
	TreeNode* m_pLeft;
	TreeNode* m_pRight;	
};
void UpDownPrintTree(TreeNode*TreeRoot)
{
     
	if(TreeRoot==NULL)
		return;
	queue<TreeNode*>Tree;
	Tree.push(TreeRoot);//先将根节点入队
	while(Tree.empty())
	{
     
		TreeNode* Node=Tree.front();
		printf("%d",Node->m_nValue);
		Tree.pop();
		if(Node->m_pLeft)//当有左子树的时候在进行入队
			Tree.push(Node->m_pLeft);
		if(Node->m_pRight)
			Tree.push(Node->m_pRight);
	}
}

2.换行打印二叉树思路

换行打印与上一题思路类似，只是在打印完一行后换行

如上图换行打印结果为
1
2 3
4 5

这次选择将打印结果存放到二维数组中，也可以选择上一题的打印方法。

具体打印思路和上面的类似。
选择二维数组形式返回，数组内以一维数组的形式储存。所以定义一个临时一维数组，将一行的数据放到临时的一维数组中，当这一行的数字打印完后，把这个数组以尾插的形式给要返回的二维数组。之后清空临时一维数组再储存第二行的数据。

确定换行的位置：
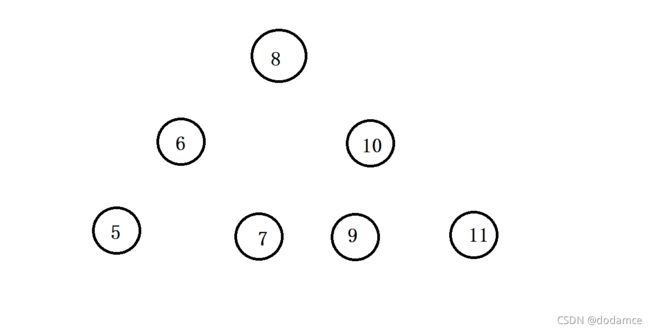
为了确定换行的位置我们需要定义两个变量，一个变量为当前一行有几个节点PreNum，另一个变量为下一行变量有几个节点NexNum。

PreNum的初值为1，因为如果节点不为空的话，第一行的节点为根节点，一定一行只有一个节点。NexNum初值为0。

当根节点入队后，根据根节点的指针根节点的左右子树指针将左右子树入队时NexNum++，再将根节点出队PreNum- -
这样当一行的数据出队完毕后NexNum为二叉树下一行的节点数。一行数据出队完毕后PreNum为0。这时将PreNum=NexNum，NexNum=0。开始统计处理下一行数据。

eg:

操作	队列数据	PreNum	NexNum
初值8	8	1	0
出8入6入10	6，10	0	2
出6入5入7	10，5，7	1	2
出10入9入10	5，7，9，11	0	4
出5	7，9，11	3	0
出7	9，11	2	0
出9	11	1	0
出11	空	0	0

如上图与上表可知，当PreNum为0时表示下一行，此时将NexNum赋值给PreNum，当队列为空时结束循环

C++代码

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
     
public:
        vector<vector<int> > Print(TreeNode* pRoot) {
     
            vector<vector<int>>ret;
            if(pRoot==nullptr)
                return ret;
            int PreNum=1;
            int NexNum=0;
            queue<TreeNode*>Tree;
            Tree.push(pRoot);//先将根节点入队列，这样PreNum初值为1
            vector<int>tmpvect;
            while(!Tree.empty())
            {
     
                TreeNode*tmp=Tree.front();
                tmpvect.push_back(tmp->val);
                if(tmp->left)//当有左子树时入队。
                {
     
                    ++NexNum;//记录下一行的节点个数
                    Tree.push(tmp->left);
                }
                if(tmp->right)
                {
     
                    ++NexNum;
                    Tree.push(tmp->right);
                }
                Tree.pop();
                --PreNum;
                if(PreNum==0)
                {
     
                    PreNum=NexNum;
                    NexNum=0;
                    ret.push_back(tmpvect);
                    tmpvect.clear();//记得将临时数组清空
                }
            }
            return ret;
        }
    
};

3.之字打印二叉树思路（栈）

如上图，之字打印二叉树的结果为
1
3 2
4 5
打印顺序左右变化

思路承接上一题，我们还是将结果保存再二维数组中
我们首先想到用队列来实现这种打印，但是因为队列先进先出，所以按上面的思路一定是先打印2节点再打印3节点。所以排除这种思路

再看如果还是按照上面的思路，先左子树再右子树的话要想打印为3 2，需要一种后进先出的数据结构栈，3相比于2后入栈，所以3优先与2出栈。我们先按照思路写下模拟表格

操作	栈数据	出栈
初始值1	1	1
1出栈2先入栈3后入栈	2 3	3
3出栈4先入栈5后入栈	2 4 5	5

这时发现问题下一个出栈的元素变成了5，但是我们想要2出栈。所以意识到节点出栈时左右节点入栈不能是同一个栈，要不然就不能让同一行的数据出栈了，例子如上图

所以我们设计两个栈，其表格分析如下
要打印的栈我们设为popTree，保存出栈节点的左右子树的栈我们设为pushTree
当popTree为空的时候说明一行结束了，这首pushTree中保存了下一行的数据

操作	popTree	pushTree	出栈元素
初始值1	1	空	1
1出栈2先入pushTree 3后入pushTree	空	2 3
交换popTree与pushTre	2 3	空	3
3出栈4先入pushTree5后入pushTree	2	4 5	2
2出栈无数据入pushTree	空	4 5
交换popTree与pushTree	4 5	空	5
5出栈无数据入栈	4	空	4
4出栈无数据入栈	空	空

发现当两个栈都为空时结束循环，但是又发现打印顺序为
1
3 2
5 4
第三行打印为5 4与我们预期的4 5不符合，正好相反。这时我们意识到要想实现每一行打印顺序不同，与数据入栈的顺序有关，第三行数据如果是右子树先入栈，左子树后入栈就正确了。

操作	popTree	pushTree	出栈元素
初始值1	1	空	1
1出栈2先入pushTree 3后入pushTree	空	2 3
交换popTree与pushTree，表示下一行，入栈顺序改变	2 3	空	3
3出栈5先入pushTree 4后入pushTree	2	5 4	2
2出栈无数据入pushTree	空	5 4
交换popTree与pushTree，表示下一行入栈顺序改变	5 4	空	4
4出栈无数据入栈	5	空	5
5出栈无数据入栈	空	空

由上可知第二行左先与右入栈，第三行右先与左入栈，第四行左先于右入栈。
如何表示换行：这时又发现当popTree与pushTree交换的时候表示换行，那么当popTree与初值相等时左优先与右入栈。当popTree与初值不同，变成了pushTree说明换行，改变入栈模式

C++代码

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
     
public:
    vector<vector<int>>ret;
    vector<vector<int> > Print(TreeNode* pRoot) {
     
        if(pRoot==nullptr)
            return ret;
        vector<int>tmp;//临时整形数组思路与上面换行打印类似
        stack<TreeNode*>Tree[2];
        int pushTree=1;//两个栈的标签，方便交换
        int popTree=0;
        Tree[popTree].push(pRoot);
        //当两个栈都为空时才结束循环
        while(!Tree[pushTree].empty()||!Tree[popTree].empty())
        {
     
            TreeNode*tmpNode=Tree[popTree].top();
            tmp.push_back(tmpNode->val);
            Tree[popTree].pop();
            if(popTree==0)//开始从左先右入栈，换行交换后popTree变为0改变入栈顺序
            {
     
                if(tmpNode->left!=nullptr)
                    Tree[pushTree].push(tmpNode->left);
                if(tmpNode->right!=nullptr)
                    Tree[pushTree].push(tmpNode->right);
            }
            else 
            {
     
                if(tmpNode->right!=nullptr)
                    Tree[pushTree].push(tmpNode->right);
                if(tmpNode->left!=nullptr)
                    Tree[pushTree].push(tmpNode->left);
            }
            if(Tree[popTree].empty())//当发现pop栈空了说明要换行了
            {
     
                ret.push_back(tmp);//将临时数组尾插到二维数组上
                swap(pushTree,popTree);//交换两个数组
                tmp.clear();//清空临时数组
            }
        }
        return ret;
    }
    
};