【存储】LSM-Tree架构
目录
概念
磁盘IO与预读
顺序写VS随机写
传统数据库加快数据访问的解决方案
B树(B-树)相关简介
B+树相关简介
LSM-Tree是什么?
一、体系结构
二、存储模型
WAL(write ahead log)
MemTable
Immutable Memtable
SSTable
三、LSM-Tree写入流程
四、LSM-Tree读取流程
LSM TREE与B树的优缺点
结论
参考资料
概念
十多年前,谷歌发布了大名鼎鼎的"三驾马车"的论文,分别是GFS(2003年),MapReduce(2004年),BigTable(2006年),为开源界在大数据领域带来了无数的灵感,其中在 “BigTable” 的论文中很多很酷的方面之一就是它所使用的文件组织方式,这个方法的名字叫 Log Structured-Merge Tree, 以下都简称LSM-Tree, LSM Tree起源于 1996 年的一篇论文《The Log-Structured Merge-Tree (LSM-Tree)》文末有官方论文链接。
LSM Tree在面对亿级别之上的海量数据的存储和检索的场景下,我们选择的数据库通常都是各种强力的NoSQL,比如Hbase,Cassandra,Leveldb,RocksDB等等,这其中前两者是Apache下面的顶级开源项目数据库,后两者分别是Google和Facebook开源的数据库存储引擎。而这些强大的NoSQL数据库都有一个共性,就是其底层使用的数据结构,都是仿照“BigTable”中的文件组织方式来实现的,也就是我们今天要介绍的LSM-Tree。介绍LSM-Tree之前,我们先简单了解下磁盘相关的知识,来方便我们后期理解LSM-Tree的优势在哪里。
磁盘IO与预读
计算机存储设备一般分为两种:内存储器(main memory)和外存储器(external memory)。
内存储器为内存,内存存取速度快,但容量小,价格昂贵,而且不能长期保存数据(在不通电情况下数据会消失)。
外存储器即为磁盘读取,磁盘读取数据靠的是机械运动,每次读取数据花费的时间可以分为寻道时间、旋转延迟、传输时间三个部分,寻道时间指的是磁臂移动到指定磁道所需要的时间,主流磁盘一般在5ms以下;旋转延迟就是我们经常听说的磁盘转速,比如一个磁盘7200转,表示每分钟能转7200次,也就是说1秒钟能转120次,旋转延迟就是1/120/2 = 4.17ms;传输时间指的是从磁盘读出或将数据写入磁盘的时间,一般在零点几毫秒,相对于前两个时间可以忽略不计。那么访问一次磁盘的时间,即一次磁盘IO的时间约等于5+4.17 = 9ms左右,听起来还挺不错的,但要知道一台500 -MIPS的机器每秒可以执行5亿条指令,因为指令依靠的是电的性质,换句话说执行一次IO的时间可以执行40万条指令,数据库动辄十万百万乃至千万级数据,每次9毫秒的时间,显然是个灾难。
考虑到磁盘IO是非常高昂的操作,计算机操作系统做了一些优化,当一次IO时,不光把当前磁盘地址的数据,而是把相邻的数据也都读取到内存缓冲区内,因为局部预读性原理告诉我们,当计算机访问一个地址的数据的时候,与其相邻的数据也会很快被访问到。每一次IO读取的数据我们称之为一页(page)。具体一页有多大数据跟操作系统有关,一般为4k或8k,也就是我们读取一页内的数据时候,实际上才发生了一次IO,这个理论对于索引的数据结构设计非常有帮助。
不同容量的存储器,访问速度差异悬殊。磁盘(ms级别)访问速度远远小于内存(ns级别)的访问速度,大约100000倍。
从以上数据中可以总结出一个道理,索引查询的数据主要受限于硬盘的I/O速度,查询I/O次数越少,速度越快,所以B树或B+树的结构才应需求而生;B树或B+树的每个节点的元素可以视为一次I/O读取,树的高度表示最多的I/O次数,在相同数量的总元素个数下,每个节点的元素个数越多,高度越低,查询所需的I/O次数越少;假设,一次硬盘一次I/O数据为8K,索引用int(4字节)类型数据建立,理论上一个节点最多可以为2000个元素,2000*2000*2000=8000000000,80亿条的数据只需3次I/O(理论值),可想而知,B树或B+树做为索引的查询效率有多高。
顺序写VS随机写
首先说机械硬盘,我先介绍一下它的存储原理。它有一个旋转的盘片和一个能沿半径方向移动的磁头。处理读取和写入请求时,首先可以根据请求的开始地址算出要处理的数据在磁盘上的位置,之后要进行以下几步工作:
- 磁头沿半径方向移动,直至移动到数据所在的柱面(相同半径的磁道组成的环面)
- 盘片高速旋转,使磁头到达数据的起始位置
- 磁头沿磁道从磁盘读取或写入数据
当一次读取的数据量很少的时候,1、2步骤带来的开销是无法忽略的,这使得随机写相对于顺序写会有巨大的性能劣势。因为在顺序写的时候,1、2步骤只需要执行一次,剩下的全是数据传输所需要的固有开销;而每次随机写的时候,前两个步骤都需要执行,带来了极大的额外开销。
传统数据库加快数据访问的解决方案
为了加速数据库数据的访问,大多传统的关系型数据库都会使用特殊的数据结构来帮助查找数据,这种数据结构叫作索引(Index)。对于传统的关系型数据库,考虑到经常需要范围查找某一批数据,因此其索引一般不使用 Hash算法,因为Hash仅仅能满足"=","IN"和"<=>"查询,不能使用范围查询 。所以通常采用的是树(Tree)结构。然而,树结构的种类很多,却不一定都适合用于做数据库索引。
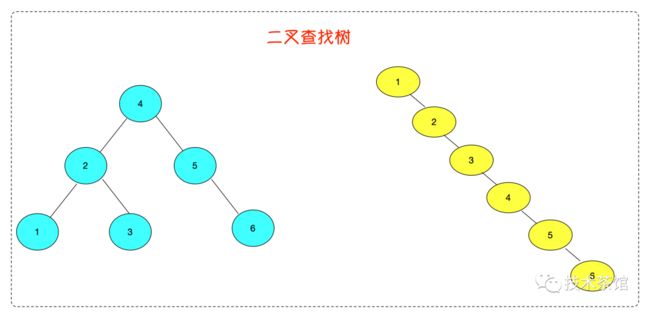
最常见的用来用查询的树结构是二叉查找树( Binary Search Tree),它就是一棵二叉有序树具有如下特征。
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 左、右子树也分别为二叉排序树;
- 没有键值相等的结点。
其优点在于实现简单,并且树在平衡的状态下查找效率能达到 O(logN); 缺点是在极端非平衡情况下查找效率会退化到 O(N),因此很难保证索引的效率。
针对上述二叉查找树的缺点,人们很自然就想到是否能用平衡二叉树(Balanced Binary Tree)来解决这个问题。但是平衡二叉树依然有个比较大的问题:它的树高为 log(N), 对于索引树来说,树的高度越高,意味着查找所要花费的访问次数越多,查询效率越低。
并且主存从磁盘读数据一般以页为单位,因此每次访问磁盘都会读取多个扇区的数据(比如 4KB大小的数据),远大于单个二叉树节点的值(字节级别),这也是造成二叉树相对索引树效率低下的原因。正因如此,人们就想到了通过增加每个树节点的度来提高访问效率,而 B+树(B+ tree)便受到了更多的关注。
B树(B-树)相关简介
了解B+树之前,我们先了解一下什么叫做B树。B树又名平衡多路(即不止两个子树)查找树,一个m阶的B树具有如下几个特征:
- 根结点至少有两个子女。
- 每个中间节点都包含k-1个元素和k个孩子,其中 m/2 <= k <= m
- 每一个叶子节点都包含k-1个元素,其中 m/2 <= k <= m
- 所有的叶子结点都位于同一层。
- 每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域分划。
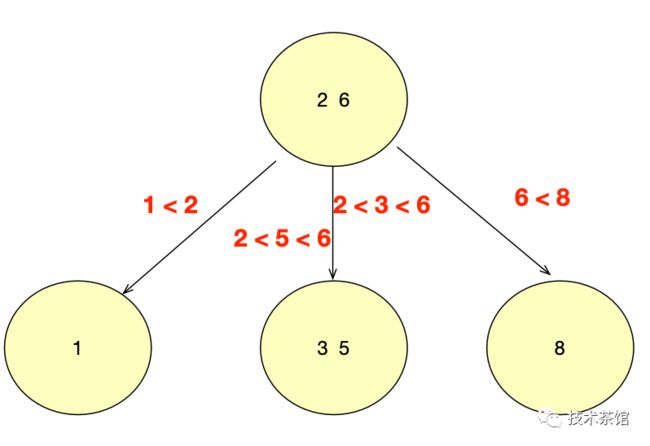
举个例子(3阶B树):
咱们看下绿色的(2, 6)节点。该节点有两个元素2和6, 又有三个孩子 1,(3, 5),8。其中1小于 元素2,(3, 5)在元素2, 6之间,8 大于(3, 5),正好符合B树的特征。
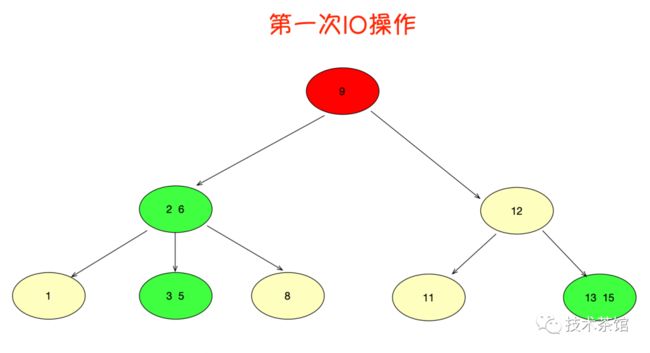
假设我们要查询的数据是5
第1次磁盘IO:
在内存中定位(和9比较)
第2次磁盘IO:
在内存中定位(和2,6比较)
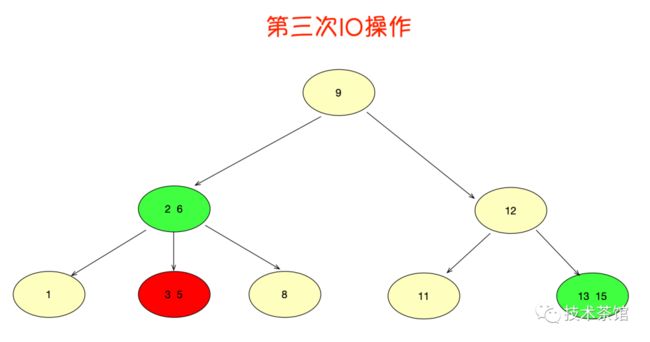
第3次磁盘IO:
在内存中定位(和3,5比较)数据5此刻找到了。
通过整个流程我们可以看出,B树在查询中的比较次数其实不比二叉查找树少,尤其当单一节点中的元素数量很多时。但是相比磁盘IO的速度,内存中的比较耗时几乎可以忽略。所以只要树的高度足够低,IO次数足够少,就可以提升查找性能。相比之下节点内部元素多一些也没有关系,仅仅是多了几次内存交互,只要不超过磁盘页的大小即可。
B+树相关简介
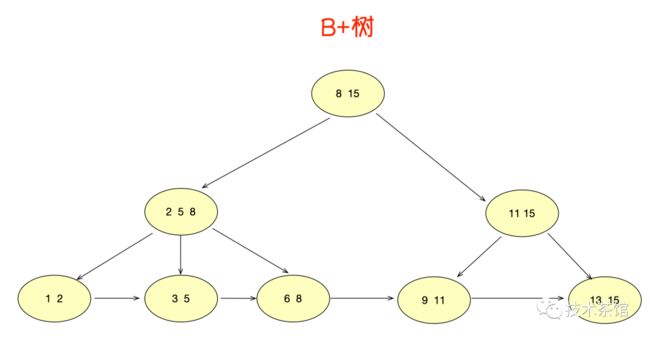
B+树是基于B树的一种变体,有着比B树更高的查询性能。一个m阶的B+树具有如下几个特征:
- 有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点。
- 所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
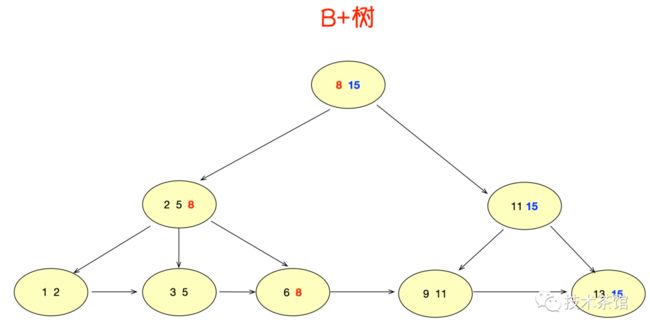
- 所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素。
在上面这棵树中, 根节点元素8是子节点2,5,8的最大元素,也是叶子节点6,8的最大元素。
在上面这棵树中, 根节点元素15是子节点11,15的最大元素,也是叶子节点13,15的最大元素。
需要注意的是,根节点的最大元素(这里是15),也就等同于整个B+树的最大元素。以后无论插入删除多少元素,始终要保持最大的元素在根节点当中。
至于叶子节点,由于父节点的元素都出现在子节点,因此所有叶子节点包含了全量元素信息。
并且每一个叶子节点都带有指向下一个节点的指针,形成了一个有序链表。
B+树还具有一个特点,这个特点是在索引之外,他就是卫星数据的位置。
所谓卫星数据,指的是索引元素所指向的数据记录,比如数据库中的某一行。在B树中,无论中间节点还是叶子节点都带有卫星数据。
B树中的卫星数据:
需要补充的是,在数据库的聚集索引(Clustered Index)中,叶子节点直接包含卫星数据。在非聚集索引(NonClustered Index)中,叶子节点带有指向卫星数据的指针。
那么B+树设计成这样有什么好处呢?
B+树的好处主要体现在查询性能上,下面我们分别通过单行查询和范围查询来做分析。
例子一:
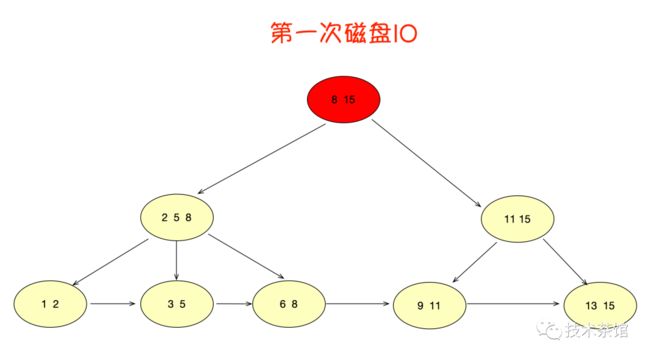
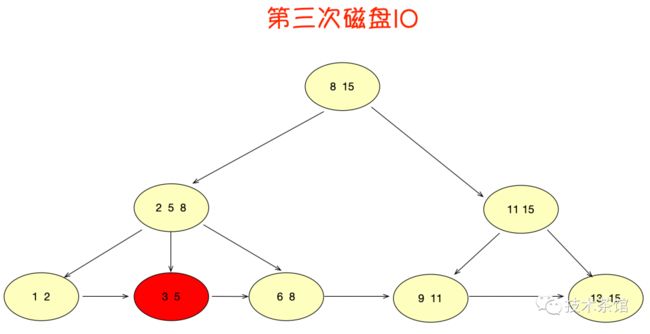
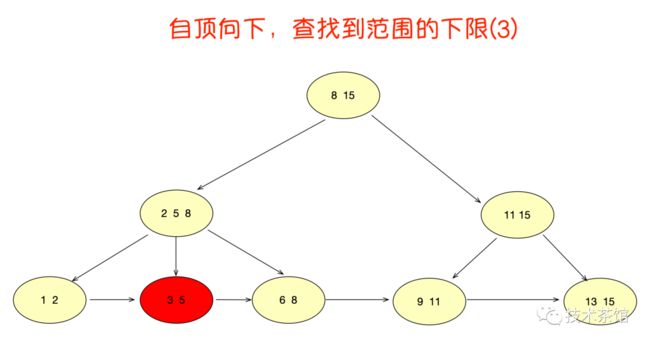
在单元素查询的时候,B+树会自顶向下逐层查找节点,最终找到匹配的叶子节点。比如我们要查找的是元素3。
虽然查询流程看起来和B树差不多。不过有两点不同。
- B+树的中间节点没有卫星数据,所以同样大小的磁盘页可以容纳更多的节点元素。这就意味着,数据量相同的情况下,B+树的结构比B树更加"矮胖",因此查询时IO次数也更少。
- B+树的查询必须最终查找到叶子节点,而B树只要找到匹配元素即可,无论匹配元素处于中间节点还是叶子节点。因此,B树的查找性能并不稳定(最好情况是只查根节点,最坏情况是查到叶子节点)。而B+树的每一次查找都是稳定的。
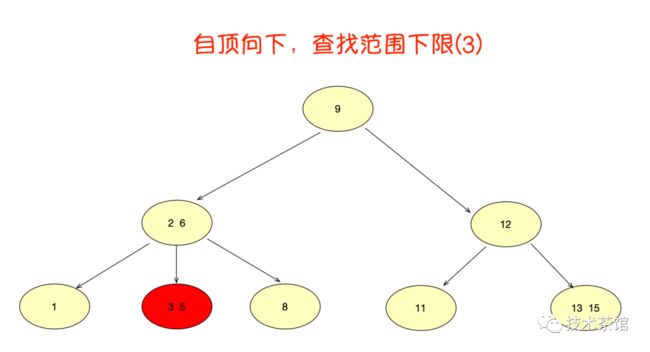
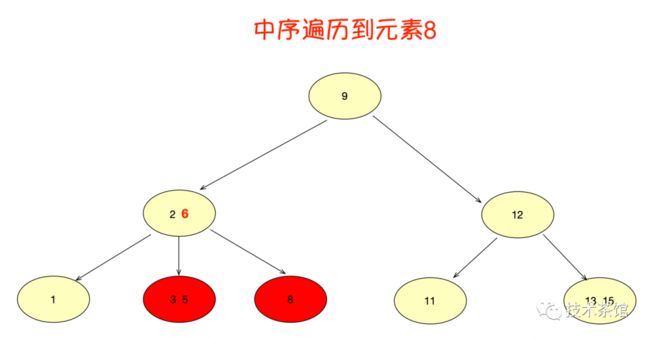
下面我们再来看看范围查询。B树如何做范围查询呢?只能依靠繁琐的中序遍历。比如我们要查找范围为3到11的元素:
例子二 :
下面我们再来看看范围查询。B树如何做范围查询呢?只能依靠繁琐的中序遍历。比如我们要查找范围为3到11的元素:
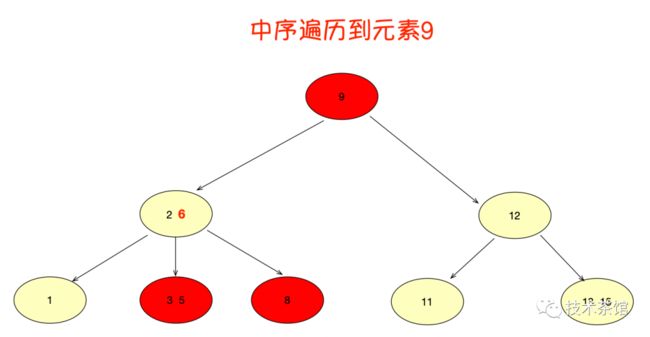
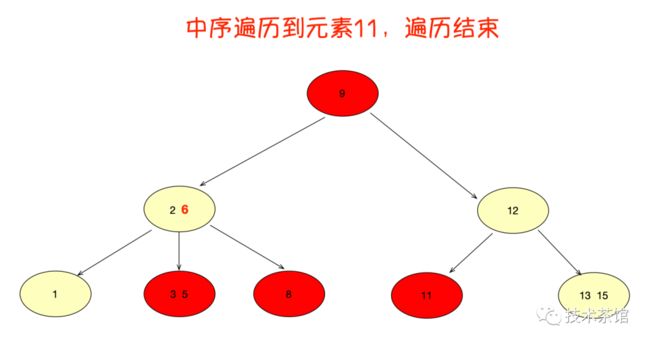
B树的范围查找过程
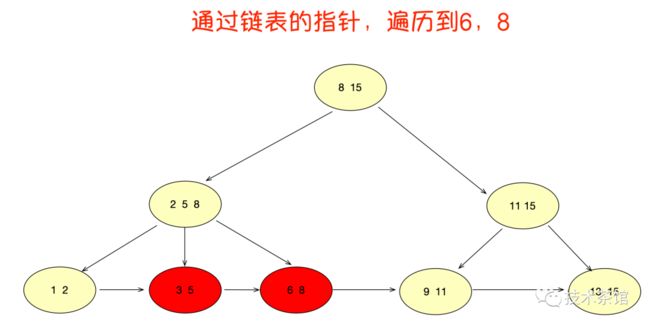
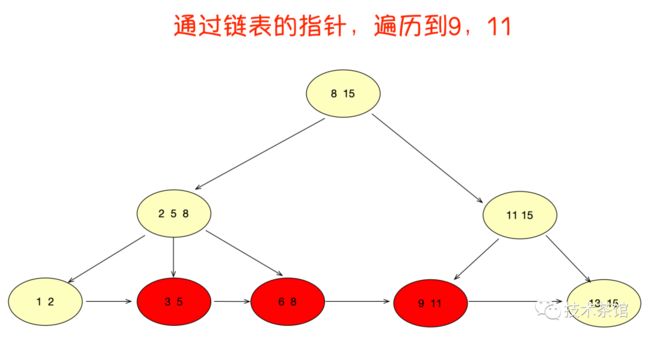
B树的范围查询确实很繁琐,反观B+树的范围查询,则要简单得多,只需要在链表上做遍历即可。
B+树的范围查找过程
综合起来,B+树相比B树优势有三个
- 单一节点存储更多的元素,使得查询的IO次数更少。
- 所有查询都要查找到叶子节点,查询性能稳定。
- 所有叶子节点形成有序链表,便于范围查询。
正是由于 B+树的上述优点,它成了传统关系型数据库的宠儿。当然,它也并非无懈可击,它的主要缺点在于随着数据插入的不断发生,叶子节点会慢慢分裂——这可能会导致逻辑上原本连续的数据实际上存放在不同的物理磁盘块位置上,在做范围查询的时候会导致较高的磁盘 IO,以致严重影响到性能。
随着B+树插入数据的时候需要较多的磁盘随机读写痛点产生, 1992年,名为日志结构( Log-Structured)的新型索引结构方法便应运而生。日志结构方法的主要思想是将磁盘看作一个大的日志,每次都将新的数据及其索引结构添加到日志的最末端,以实现对磁盘的顺序操作,从而提高索引性能。不过,日志结构方法也有明显的缺点,随机读取数据时效率很低。直到1996年,一篇名为 Thelog-structured merge-tree(LSM-tree)的论文创造性地提出了日志结构合并树( Log-Structured Merge-Tree)的概念,该方法既吸收了日志结构方法的优点,又通过将数据文件预排序克服了日志结构方法随机读性能较差的问题。下面我们介绍一下什么是LSM-TREE。
LSM-Tree是什么?
LSM-Tree全称是Log Structured Merge Tree,是一种分层,有序,面向磁盘的数据结构,其核心思想是充分了利用了,磁盘批量的顺序写要远比随机写性能高出很多。
核心思想的核心就是放弃部分读能力,换取写入的最大化能力。LSM Tree ,这个概念就是结构化合并树的意思,它的核心思路其实非常简单,就是假定内存足够大,因此不需要每次有数据更新就必须将数据写入到磁盘中,而可以先将最新的数据驻留在内存中,等到积累到最后多之后,再使用归并排序的方式将内存内的数据合并追加到磁盘队尾(因为所有待排序的树都是有序的,可以通过合并排序的方式快速合并到一起)。
日志结构的合并树(LSM-tree)是一种基于硬盘的数据结构,与B-tree相比,能显著地减少硬盘磁盘臂的开销,并能在较长的时间提供对文件的高速插入(删除)。然而LSM-tree在某些情况下,特别是在查询需要快速响应时性能不佳。通常LSM-tree适用于索引插入比检索更频繁的应用系统。Bigtable在提供Tablet服务时,使用GFS来存储日志和SSTable,而GFS的设计初衷就是希望通过添加新数据的方式而不是通过重写旧数据的方式来修改文件。而LSM-tree通过滚动合并和多页块的方法推迟和批量进行索引更新,充分利用内存来存储近期或常用数据以降低查找代价,利用硬盘来存储不常用数据以减少存储代价。
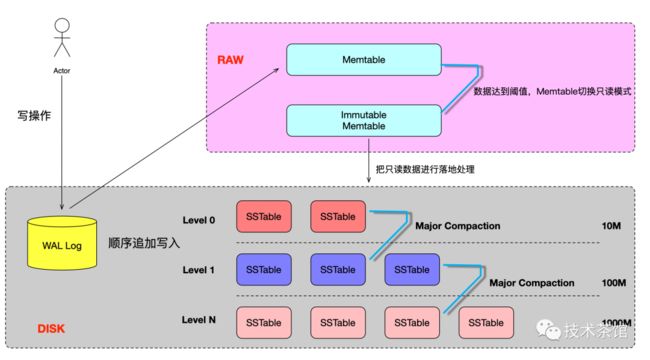
下面我们看下LSM Tree的体系结构图,来了解下LSM-Tree有哪些组成元素。
一、体系结构
二、存储模型
那么根据上面LSM-Tree的体系结构图,我们大致可以把LSM-Tree划分为如下几个部分。
WAL(write ahead log)
WAL(write ahead log)也称预写log,包括mysql的Binlog等,在设计数据库的时候经常被使用,当插入一条数据时,数据先顺序写入 WAL 文件中,之后插入到内存中的 MemTable 中。这样就保证了数据的持久化,不会丢失数据,并且都是顺序写,速度很快。当程序挂掉重启时,可以从 WAL 文件中重新恢复内存中的 MemTable。
MemTable
MemTable 对应的就是 WAL 文件,是该文件内容在内存中的存储结构,通常用 SkipList 来实现。MemTable 提供了 k-v 数据的写入、删除以及读取的操作接口。其内部将 k-v 对按照 key 值有序存储,这样方便之后快速序列化到 SSTable 文件中,仍然保持数据的有序性。
Immutable Memtable
Immutable Memtable 就是在内存中只读的 MemTable,由于内存是有限的,通常我们会设置一个阀值,当 MemTable 占用的内存达到阀值后就自动转换为 Immutable Memtable,Immutable Memtable 和 MemTable 的区别就是它是只读的,系统此时会生成新的 MemTable 供写操作继续写入。之所以要使用 Immutable Memtable,就是为了避免将 MemTable 中的内容序列化到磁盘中时会阻塞写操作。
SSTable
SSTable(Sorted String Table) SSTable是一种拥有持久化,有序且不可变的的键值存储结构,它的key和value都是任意的字节数组,并且了提供了按指定key查找和指定范围的key区间迭代遍历的功能。SSTable内部包含了一系列可配置大小的Block块,典型的大小是64KB,关于这些Block块的index存储在SSTable的尾部,用于帮助快速查找特定的Block。当一个SSTable被打开的时候,index会被加载到内存,然后根据key在内存index里面进行一个二分查找,查到该key对应的磁盘的offset之后,然后去磁盘把响应的块数据读取出来。当然如果内存足够大的话,可以直接把SSTable直接通过MMap的技术映射到内存中,从而提供更快的查找。
三、LSM-Tree写入流程
- 当收到一个写请求时,会先把该条数据记录在WAL Log里面,用作故障恢复。
- 当写完WAL Log后,会把该条数据写入内存的SSTable里面(删除是墓碑标记,更新是新记录一条的数据),也称Memtable。注意为了维持有序性在内存里面可以采用红黑树或者跳跃表相关的数据结构。
- 当Memtable超过一定的大小后,会在内存里面冻结,变成不可变的Memtable,同时为了不阻塞写操作需要新生成一个Memtable继续提供服务。
- 把内存里面不可变的Memtable给dump到到硬盘上的SSTable层中,此步骤也称为Minor Compaction,这里需要注意在L0层的SSTable是没有进行合并的,所以这里的key range在多个SSTable中可能会出现重叠,在层数大于0层之后的SSTable,不存在重叠key。
- 当每层的磁盘上的SSTable的体积超过一定的大小或者个数,也会周期的进行合并。此步骤也称为Major Compaction,这个阶段会真正 的清除掉被标记删除掉的数据以及多版本数据的合并,避免浪费空间,注意由于SSTable都是有序的,我们可以直接采用merge sort进行高效合并。
四、LSM-Tree读取流程
LSM Tree 的读取效率并不高,当需要读取指定 key 的数据时,先在内存中的 MemTable 和 Immutable MemTable 中查找,如果没有找到,则继续从 Level 0 层开始,找不到就从更高层的 SSTable 文件中查找,如果查找失败,说明整个 LSM Tree 中都不存在这个 key 的数据。如果中间在任何一个地方找到这个 key 的数据,那么按照这个路径找到的数据都是最新的。
在每一层的 SSTable 文件的 key 值范围是不重复的,所以只需要查找其中一个 SSTable 文件即可确定指定 key 的数据是否存在于这一层中。Level 0 层比较特殊,因为数据是 Immutable MemTable 直接写入此层的,所以 Level 0 层的 SSTable 文件的 key 值范围可能存在重复,查找数据时有可能需要查找多个文件。
如果SSTable的分层越多,那么最坏的情况下要把所有的分层扫描一遍。有没有什么优化方案呢,在BigTable的论文中提出了几个方式。
压缩
SSTable 是可以启用压缩功能的,并且这种压缩不是将整个 SSTable 一起压缩,而是根据 locality 将数据分组,每个组分别压缩,这样的好处当读取数据的时候,我们不需要解压缩整个文件而是解压缩部分 Group 就可以读取。
缓存
因为SSTable在写入磁盘后,除了Compaction之外,是不会变化的,所以我可以将Scan的Block进行缓存,从而提高检索的效率。
索引,Bloom filters
正常情况下,一个读操作是需要读取所有的 SSTable 将结果合并后返回的,但是对于某些 key 而言,有些 SSTable 是根本不包含对应数据的,因此,我们可以对每一个 SSTable 添加 Bloom Filter,因为布隆过滤器在判断一个SSTable不存在某个key的时候,那么就一定不会存在,利用这个特性可以减少不必要的磁盘扫描。
合并(Compaction)
随着数据写入不断增多,转储次数也会不断增多,进而转储SSTable也会越来越多。然而,太多SSTable会导致数据查询IO次数增多,因此后台尝试着不断对这些SSTable进行合并,这个合并过程称为Compaction。Compaction分为两类:Minor Compaction和Major Compaction。
Minor Compaction是指选取一个或多个小的、相邻的转储SSTable与0个或多个Frozen Memtable,将它们合并成一个更大的SSTable。一次Minor Compaction的结果是更少并且更大的SSTable。
Major Compaction是指将所有的转储SSTable和一个或多个Frozen Memtable合并成一个SSTable,这个过程会清理被删除的数据。一般情况下,Major Compaction时间会持续比较长,整个过程会消耗大量系统资源,对上层业务有比较大的影响。
随着数据写入不断增加,Minor Freeze不断触发,转储数据不断增多,一次查询可能需要越来越多的IO操作,读取延时也在不断变大。而执行Minor Compaction会使得转储文件数基本稳定,进而IO Seek次数会比较稳定,延迟就会稳定在一定范围。然而,Minor Compaction操作重写文件会带来很大的带宽压力以及短时间IO压力。因此可以认为,Minor Compaction就是使用短时间的IO消耗以及带宽消耗换取后续查询的低延迟。
为了换取后续查询的低延迟,除了短时间的读放大之外,Compaction对写入也会有很大的影响。当写请求非常多,导致不断触发Minor Compaction生成转储SSTable,多次Minor Freeze会触发Major Freeze,从而导致Major Compaction,但Compaction的速度远远跟不上数据写入速度,Memtable内存不足时,会限制用户数据写入。如果Compaction消耗大量IO和带宽,也会导致读性能急剧下降。为了避免这种情况,在Memtable内存紧张时候会限制写请求的速度。
Minor Compaction释放Memtable内存,清理不必要的多版本数据,同时保证转储SSTable数量稳定,降低读延迟;Major Compaction清除删除和过期的数据,有效降低存储空间,也可以有效降低读取时延。Compaction会使得数据读取延迟一直比较平稳,但付出的代价是大量的读延迟毛刺和一定的写阻塞。
LSM TREE与B树的优缺点
传统关系型数据采用的底层数据结构是B+树,那么同样是面向磁盘存储的数据结构LSM-Tree相比B+树有什么异同之处呢?
LSM-Tree的设计思路是,将数据拆分为几百M大小的Segments,并是顺序写入。
B+Tree则是将数据拆分为固定大小的Block或Page, 一般是4KB大小,和磁盘一个扇区的大小对应,Page是读写的最小单位。
在数据的更新和删除方面,B+Tree可以做到原地更新和删除,这种方式对数据库事务支持更加友好,因为一个key只会出现一个Page页里面,但由于LSM-Tree只能追加写,并且在L0层key的rang会重叠,所以对事务支持较弱,只能在Segment Compaction的时候进行真正地更新和删除。
因此LSM-Tree的优点是支持高吞吐的写(可认为是O(1)),这个特点在分布式系统上更为看重,当然针对读取普通的LSM-Tree结构,读取是O(N)的复杂度,在使用索引或者缓存优化后的也可以达到O(logN)的复杂度。
而B+tree的优点是支持高效的读(稳定的OlogN),但是在大规模的写请求下(复杂度O(LogN)),效率会变得比较低,因为随着insert的操作,为了维护B+树结构,节点会不断的分裂和合并。操作磁盘的随机读写概率会变大,故导致性能降低。
还有一点需要提到的是基于LSM-Tree分层存储能够做到写的高吞吐,带来的副作用是整个系统必须频繁的进行compaction,写入量越大,Compaction的过程越频繁。而compaction是一个compare & merge的过程,非常消耗CPU和存储IO,在高吞吐的写入情形下,大量的compaction操作占用大量系统资源,必然带来整个系统性能断崖式下跌,对应用系统产生巨大影响,当然我们可以禁用自动Major Compaction,在每天系统低峰期定期触发合并,来避免这个问题。
结论
LSM树的设计思想非常朴素,简而言之就是将对数据的修改增量保持在内存中,达到指定的大小限制后将这些修改操作批量写入磁盘,其具体做法是把一棵大树拆分成N棵小树,它首先将内容写入内存中,随着小树越来越大,当达到内存写入阈值后,内存中的小树会flush到磁盘中,这样磁盘中的树定期做merge操作,合并成一棵稳定的大树(优化数据的读性能)。当进行数据读取时,需要合并磁盘中历史数据和内存中最近修改操作,综合两者才能进行完整的数据查找操作。
批量操作减少了磁盘磁臂的移动次数降低了进行数据插入时磁盘磁臂的开销,所以写入性能大大提升,同时读性能有所下降,LSM在进行需要即时响应的操作时会损失I/O效率,最适用于索引插入比查询操作多的情况。
目前分布式数据库使用LSM-Tree做底层存储架构的比较多,比如说目前阿里的OceanBase, Hbase, ClickHouse(采用用的也是类似LSM-Tree的技术)。
参考资料
1. https://www.cs.umb.edu/~poneil/lsmtree.pdf