物理层基础 - 通信模型

引言

物理层作为无线通信协议的支撑性底层对通信性能起着至关重要的作用，可以看到几乎所有实现通信系统跨代的技术革新基本上都发生在物理层上，而物理层的底层就是信号的调制和解调，所谓的频分复用，时分复用甚至MIMO技术代表的空分复用无不需要建立在信号调解功能之上。

一、调制解调类型

调制的实质目的只是为了得到便于发射的无线信号，因此调后信号均为模拟信号。

按照调前信号的类型，调解可分为：数字调解、模拟调解。

而依照实际通信系统的组成结构，调解又可划分为：基带调解、射频调解。

基带调解 - 数字调解、模拟调解
射频调解 - 模拟调解

依照基带调解采用的方式不同可大体将通信系统划分为：数字通信系统、模拟通信系统。

二、通信模型

1.模拟通信系统

模拟波形 -<模拟调制>- 射频波形 -<模拟解调>- 模拟波形

2.数字通信系统

数字比特 -<编码调制>- 数字比特 -<星座映射/调制>- 复值符号(I/Q) -<脉冲成形滤波器2>-* 基带波形*2 -<IQ调制>- 射频波形 -<IQ解调>- 基带波形*2 -<抽样判决>- 复值符号(I/Q) -<星座逆映射/解调>- 数字比特 -<编码解调>- 数字比特

射频调制或者模拟调制的本质就是将基带信号的频谱搬移到射频频率，常用方法就是乘以cos(2*PI*fc*t)实现频谱搬移。

数字调解的实质就是星座的映射与逆映射，因此数字调解也称为星座调解，基于IQ方法实现的数字调制将多个数字比特映射为一个复值符号，随后复值符号的实虚部按两路脉冲成形为两路基带信号，在通过IQ模拟调制频谱搬移到射频处辐射传播。

数字通信系统中符号周期的概念比较重要，因为多个数字比特映射为的复值符号经脉冲成形得到波形的持续时间是构成系统子帧/帧的基本时间粒子。在工程上还有用眼图来观察基带波形中单个符号周期内的波形变化并以此判断是否出现码间串扰。

三、IQ调解 - 数字/模拟调解的基础

IQ调解是非常重要的工程方法，目前商用的通信系统所采用的调解方式均基于IQ调解技术，基于IQ的数字调解就是所谓的星座调解，基于IQ的模拟调解因为可以在相同带宽下同时传送两路基带信号更是取代基于希尔伯特变换的单边带调解。

详细推导可参考http://blog.csdn.net/u013597671/article/details/77019187

IQ调制原理：

假设I路输入为a，Q路输入为b，则IQ调制输出为a*cos(2*PI*fc*t) - b*sin(2*PI*fc*t)。

将IQ路输入记为a+j*b，IQ调制为值e^j*2*PI*fc*t的乘法器，则IQ调制的数学表达即为Re{(a+j*b) * e^j*2*PI*fc*t}。

IQ解调原理：

接收端I路首先实现乘法Re{(a+j*b) * e^j*2*PI*fc*t} * cos(2*PI*fc*t)，从实现上可知输入a的频谱经历了两次相同范围的频谱搬移，因此对上述信号过低通滤波即可得到a。

同样，接收端Q路首先实现乘法Re{(a+j*b) * e^j*2*PI*fc*t} * -sin(2*PI*fc*t)，从实现上可知输入b的频谱也经历了两次相同范围的频谱搬移，因此对上述信号过低通滤波即可得到b。

IQ调解的优势在于两路数据的复用传输。

星座调解和星座图：

如果a，b是持续一段时间的数字信号，则此时IQ调解即星座调解，此时a+j*b在复平面上形成的分布图即为星座图，多位数字比特构成的码元与复值的映射关系即为星座映射。

由此如果N位二进制比特构成码元，则共有2^N中码元组合，因此也需要2^N个星座点或者说2^N个复值来保证一一应对关系。

星座图里隐含的数学原理：

根据和差化积公式可得a*cos(2*PI*fc*t) - b*sin(2*PI*fc*t) = A*cos(2*PI*fc*t + P)，式中幅值A和初始相位P分别对应(a, b)在复平面的里的模和相角。

IQ模拟调解：

如果a，b分别是模拟信号，此时实现的IQ调解就是模拟调解，基本上IQ模拟调解要配合星座调解使用，因此两者统称为IQ调解方案。

四、脉冲成形与眼图

脉冲成形是生成基带波形的重要环节，脉冲成形中所谓的脉冲是指调制后的数字比特按照采样频率形成的类冲激脉冲，冲激脉冲虽然也可以视为特殊的模拟信号但不适合无线传输，因此需要对冲激脉冲进行插值使之变成连续的模拟信号，即所谓的“成形”，脉冲成形器实质上是滤波器，因此成形波形指其单位冲激响应。

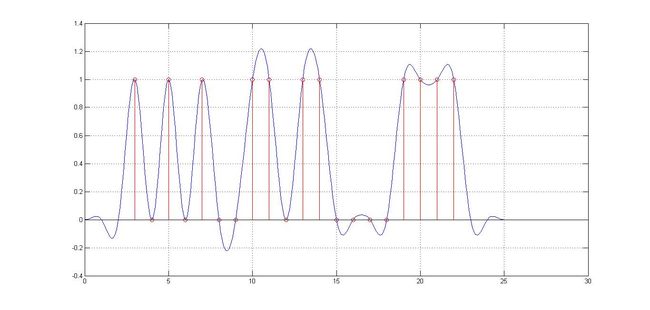
最容易想到的成形波形是矩形方波，因此冲激脉冲经过矩形波成形后形成的基带波形就是方波脉冲，但方波脉冲在实际中无法抵抗码间串扰，即前后码元方波电平会相互干扰导致严重的波形失真，在实际应用的成形滤波器往往是所谓的升余弦滤波器。

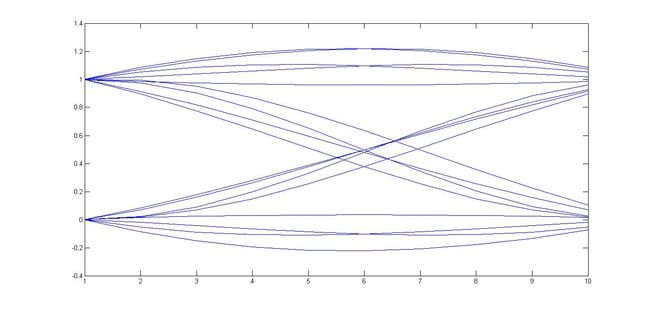
所谓的眼图即在工程上通过示波器叠加显示基带码元周期内的升降波形来判断是否存在码间串扰。

clear all
close all
Fd = 1
Fs = 10
r = 0.5
delay = 3

[num, den] = rcosine(Fd,Fs,'default',r,delay);

x = randint(1,20)

[y,ty] = rcosflt(x,Fd,Fs,'default',r,delay);

% figure;
% impz(num,1)
% grid on;
% figure
% stem(num)
% grid on;

t = delay*Fd:(length(x)+delay -1) *Fd

figure
plot(ty,y)
hold on
stem(t,x,'-r')
grid on

% figure
% stem(x)

k = 1
for ii=1:length(x)     
for jj=1:Fs/Fd          
samp(k)=x(ii);         
k=k+1;     
end 
end  
m = conv(samp,num)
% figure
% stem(ty,m)


figure
plot(y)
grid on

figure
for k = 5:floor(length(y)/Fs/Fd)-5

ss = y(k*Fs/Fd+1:(k+1)*Fs/Fd);    
plot(ss);     
hold on; 
end  


figure
plot(y)
grid on
for k = 5:floor(length(y)/Fs/Fd)-5
hold on
stem(k*Fs/Fd+1,1)
hold on
stem((k+1)*Fs/Fd,1)
end  

figure

for k = t
    ss = y(k*Fs/Fd+1:(k+1)*Fs/Fd+1)
    plot(ss)
    hold on 
end

五、LTE UL/DL 框图

1. OFDM/DL

digital bit –<constellation mapping>– complex symbol –<RE mapping, serial to parallel>– RB diagram –<IFFT, N > Nof subcarriers, parallel to serial>– N complex –<add CP>– N+L complex –<pulse shaping*2>– baseband wave*2 –<IQ modulating>– RF wave

2. SC-FDMA/UL

digital bit –<constellation mapping>– complex symbol –<DFT, Nof subcarriers>– complex symbol(frequency-domain) –<RE mapping, serial to parallel>– RB diagram –<IFFT, N > Nof subcarriers, parallel to serial>– N complex –<add CP>– N+L complex –<pulse shaping*2>– baseband wave*2 –<IQ modulating>– RF wave