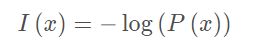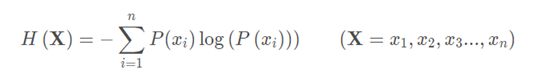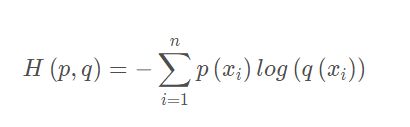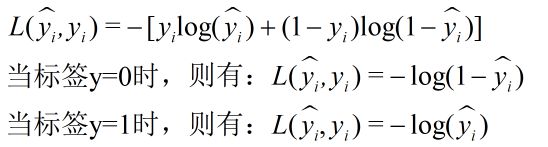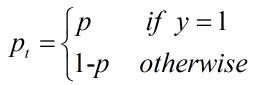交叉熵损失函数（信息量、信息熵、KL散度）_Focal Loss_

本人在学习Focal Loss时忘记了交叉熵损失的来源，几经阅读其他博文才了解清楚交叉熵的身世，本文是参考别人的博客所写，主要是怕自己忘记，所以写下此博文，方便以后翻阅。

Focal Loss的内容可参考我的下一篇博文：

https://blog.csdn.net/weixin_42649699/article/details/118255143

信息量

信息奠基人香农（Shannon）认为“信息是用来消除随机不确定性的东西”，也就是说衡量信息量的大小就是看这个信息消除不确定性的程度。

总结来说就是：信息量的大小与可预见的概率之间成反比。 信息量越大，可预见的概率越大；信息量越小，可预见的概率越小。

设某一事件发生的概率为P(x)，其信息量表示为：

其中，I(X)表示信息量，这里log表示以e为底的自然对数，P表示事件发生的概率。

信息熵

信息熵也被称为熵，用来表示所有信息量的期望。期望是试验中每次可能结果的概率 乘以 其信息量 的总和。

信息熵的表达式如下：

其中，H（X）表示信息熵，P表示事件发生的概率，-log（P）表示信息量

相对熵（KL散度）

如果对于同一个随机变量X有两个单独的概率分布P(x)和Q(x)，则我们可以使用KL散度来衡量这两个概率分布之间的差异。 相对熵的表达式如下：

KL散度越小，表示P(x)与Q(x)的分布更加接近，可以通过反复训练Q来使Q的分布逼近P .

这就有点像深度学习中的有监督学习了吧，即将P看作是样本的标签，Q看作是训练样本，使用相对熵（交叉熵损失函数）反复训练Q，让Q去逼近P。

交叉熵

通过拆解KL散度的表达式来推导交叉熵表达式：

其中，蓝色框表示信息熵，红色框表示为交叉熵，即可得到：KL散度 = 交叉熵 - 信息熵

交叉熵的表达式如下：

重新总结一下上面的推导：首先，KL散度的值表示真实概率分布P(x)与预测概率分布Q(x)之间的差异，值越小表示预测的结果越好。其次，在实际的应用中，输入数据与标签往往是已经确定，即P(x)已经确定下来了，所以信息熵（蓝色框框）在这里就是一个常量，可以不参与运算。

最后，KL散度表达式就可以写成： KL散度 = 常数 + 交叉熵 ---------->  KL散度 ≈ 交叉熵

由于最小化KL散度就能得到更好的预测结果，也就相当于最小化交叉熵可以得到更优的预测结果。所以，在深度学习中常常使用交叉熵损失函数来计算loss，将loss最小化就能让样本逼近标签。

总结：

交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度，在深度学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小，模型预测效果就越好。

交叉熵在分类问题中常常与softmax是标配，softmax将输出的结果进行处理，使其多个分类的预测值和为1，再通过交叉熵来计算损失。

————————————————————————————————————————

最后附上交叉熵和二值交叉熵的形式：

交叉熵的标准形式

 

 

二值交叉熵-标准形式

用于图像二分类时，标签y的取值为{0,1}，预测值y帽的取值范围为[0,1]，则有二值交叉熵损失函数表达式：

二值交叉熵-简写形式

在论文中经常会看到如下形式的二值交叉熵，其中还p是预测概率，y是真实标签：

将上述公式再次简写：

其中：

参考的博客：https://blog.csdn.net/b1055077005/article/details/100152102