深度学习---从入门到放弃（三)多层感知器MLP

深度学习—从入门到放弃（三)多层感知器MLP

1.MLP简介

正式进入MLP之前，我们先来看看单个神经元组成的线性神经网络，由上图可知单个神经元的神经网络无法解决像XOR这样的非线性问题。这个时候MLP就出场了！

多层感知机（MLP，Multilayer Perceptron）也叫人工神经网络（ANN，Artificial Neural Network），除了输入输出层，它中间可以有多个隐藏层，最简单的MLP只含一个隐藏层，即三层的结构。

MLP最特殊的地方就在于这个隐藏层：隐藏层的激活函数例如ReLU、Tanh、sigmoid都能够给神经元引入非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以利用到更多的非线性模型中。

上图为利用一个隐藏层的MLP解决XOR问题的例子。

2.ReLU

ReLU，正如之前所提到的，是MLP隐藏层激活函数的一种。

ReLU可以理解为一组分段函线性函数的集合，$y(x)=max(0,x+b)$，其中b为x轴的输入的负数，按照这样的规律我们可以将上图拆分成 :
$ReLU(x+1),ReLU(x),ReLU(x-1)$
除此之外我们需要结合原函数点和点之间的斜率来进行线性修正，即combination_weights：

 prev_slope = 0
 for i in range(n_relus):
    delta_x = x_train[i+1] - x_train[i]
    slope = (y_train[i+1] - y_train[i]) / delta_x
    combination_weights[i] = slope - prev_slope
    prev_slope = slope

最后只需将combination_weights与relu点乘，便可得出最终结果。
有关其他激活函数

3.Pytorch实现简单MLP

class Net(nn.Module):
  def __init__(self, actv, input_feature_num, hidden_unit_nums, output_feature_num):
    super(Net, self).__init__()
    self.input_feature_num = input_feature_num # save the input size for reshapinng later
    self.mlp = nn.Sequential() # 初始化MLP的所有层

    in_num = input_feature_num # initialize the temporary input feature to each layer
    for i in range(len(hidden_unit_nums)): # 创建hidden_unit_nums个隐藏层

      out_num = hidden_unit_nums[i] # 定位目前处在循环的隐藏层
      layer = nn.Linear(in_num, out_num) # 用nn.Linear定义层
      in_num = out_num # 定位下一个隐藏层，此时input_num变为上一层output_num
      self.mlp.add_module('Linear_%d'%i, layer) # 添加到模型并命名

      actv_layer = eval('nn.%s'%actv) # 激活函数 (eval 可以将object转换为str)
      self.mlp.add_module('Activation_%d'%i, actv_layer) # 添加到模型并命名

    out_layer = nn.Linear(in_num, output_feature_num) # 创建输出层
    self.mlp.add_module('Output_Linear', out_layer) #添加到模型并命名

  def forward(self, x):
    # reshape inputs to (batch_size, input_feature_num)
    # just in case the input vector is not 2D, like an image!
    x = x.view(-1, self.input_feature_num)

    logits = self.mlp(x) # 指定了当数据通过网络时网络需要进行的计算
    return logits


input = torch.zeros((100, 2))
net = Net(actv='LeakyReLU(0.1)', input_feature_num=2, hidden_unit_nums=[100, 10, 5], output_feature_num=1).to(DEVICE)
y = net(input.to(DEVICE))

我们这里实现了一个有三个隐藏层，激活函数为leakyReLU的MLP。

4.MLP应用于分类任务

4.1交叉熵损失

交叉熵是用来衡量两个概率分布的距离(也可以叫差别)。只要把p作为正确结果(如[0，0，0，1，0，0])，把q作为预测结果(如[0.1，0.1，0.4，0.1，0.2，0.1])，就可以得到两个概率分布的交叉熵了，交叉熵值越低，表示两个概率分布越靠近。
交叉熵损失一般作为深度学习分类任务的目标函数。

4.2 数据准备

def create_spiral_dataset(K, sigma, N):

  # Initialize t, X, y
  t = torch.linspace(0, 1, N)
  X = torch.zeros(K*N, 2)
  y = torch.zeros(K*N)

  # Create data
  for k in range(K):
    X[k*N:(k+1)*N, 0] = t*(torch.sin(2*np.pi/K*(2*t+k)) + sigma*torch.randn(N))
    X[k*N:(k+1)*N, 1] = t*(torch.cos(2*np.pi/K*(2*t+k)) + sigma*torch.randn(N))
    y[k*N:(k+1)*N] = k

  return X, y


# Set parameters
K = 4
sigma = 0.16
N = 1000

set_seed(seed=SEED)
X, y = create_spiral_dataset(K, sigma, N)
plt.scatter(X[:, 0], X[:, 1], c = y)
plt.show()

4.2.1 Pytorch训练集测试集随机划分

1.shuffle
torch.randperm(N) ：返回一个0到n-1的数组

def shuffle_and_split_data(X, y, seed):
  # set seed for reproducibility
  torch.manual_seed(seed)
  # Number of samples
  N = X.shape[0]
  # Shuffle data
  shuffled_indices = torch.randperm(N)   #返回一个0到n-1的数组
  X = X[shuffled_indices]
  y = y[shuffled_indices]

  # Split data into train/test
  test_size = int(0.2 * N)    # 20%作为测试集
  X_test = X[:test_size]
  y_test = y[:test_size]
  X_train = X[test_size:]
  y_train = y[test_size:]

  return X_test, y_test, X_train, y_train

4.3 训练模型

def train_test_classification(net, criterion, optimizer, train_loader,
                              test_loader, num_epochs=1, verbose=True,
                              training_plot=False, device='cpu'):

  net.train()
  training_losses = []
  for epoch in tqdm(range(num_epochs)):  # loop over the dataset multiple times
    running_loss = 0.0
    for i, data in enumerate(train_loader, 0):
      # get the inputs; data is a list of [inputs, labels]
      inputs, labels = data
      inputs = inputs.to(device).float()
      labels = labels.to(device).long()
      ###梯度下降
      # zero the parameter gradients
      optimizer.zero_grad()

      # forward + backward + optimize
      outputs = net(inputs)

      loss = criterion(outputs, labels)
      loss.backward()
      optimizer.step()
      ###梯度下降
      # print statistics
      if verbose:
        training_losses += [loss.item()]

  net.eval()
  def test(data_loader):
    correct = 0
    total = 0
    for data in data_loader:
      inputs, labels = data
      inputs = inputs.to(device).float()
      labels = labels.to(device).long()

      outputs = net(inputs)
      _, predicted = torch.max(outputs, 1)
      total += labels.size(0)
      correct += (predicted == labels).sum().item()

    acc = 100 * correct / total
    return total, acc

  train_total, train_acc = test(train_loader)
  test_total, test_acc = test(test_loader)

  if verbose:
    print(f"Accuracy on the {train_total} training samples: {train_acc:0.2f}")
    print(f"Accuracy on the {test_total} testing samples: {test_acc:0.2f}")

  if training_plot:
    plt.plot(training_losses)
    plt.xlabel('Batch')
    plt.ylabel('Training loss')
    plt.show()

  return train_acc, test_acc

以上为构建train_test_classification功能，包含了对于训练数据权重的梯度下降，以及每一epoch的损失变化的计算。

set_seed(SEED)
net = Net('ReLU()', X_train.shape[1], [128], K).to(DEVICE)#用的我们之前定义的简单MLP
criterion = nn.CrossEntropyLoss()#目标函数为交叉熵损失
optimizer = optim.Adam(net.parameters(), lr=1e-3)#优化器为Adam优化器
num_epochs = 100#训练epoch为100

_, _ = train_test_classification(net, criterion, optimizer, train_loader,
                                 test_loader, num_epochs=num_epochs,
                                 training_plot=True, device=DEVICE)

5. MLP宽度 vs 深度

1.MLP的深度：
神经网络的深度，之前也说过，指的就是网络中的层数，放在MLP里就是指隐藏层的数量。那么隐藏层的数量是不是越多越有利于我们解决问题呢？

从上图中我们不难看出随着我们网络中权重的方差增大，网络中数据的混乱程度也越大，而这种混乱状态随着网络深度的增加而变得明显。换言之，增大的权重方差也就意味着$x({\delta }_w,{\delta }_b)>1$也就是说在梯度下降的反向传播过程中可能会造成梯度爆炸。同样$x({\delta }_w,{\delta }_b)<1$会造成梯度消失

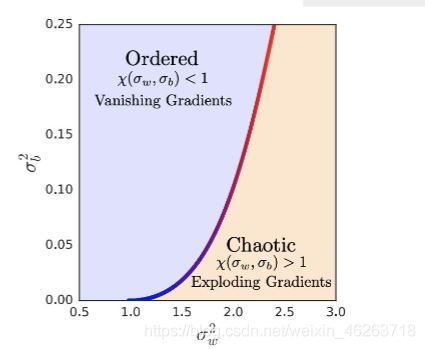
2.MLP的宽度
神经网络的宽度是指每层中神经元的数量，浅层神经网络可以通过指数级增加自己每层神经元的个数来达到和深层神经网络相同的效果，但是模型的可学习性通常会大打折扣，因此一般不会用单纯的浅层神经网络。

5.1 MLP深度与模型效果的关系

结合上文提到的对于深度的理解我们可以发现对于深层MLP而言，隐藏层的数量不是越多越好，存在一个最优隐藏层数。

5.2 MLP宽度与模型效果的关系

在这里我们先建立一个单层神经网络，为了增加网络的宽度，我们选择在网络中添加多项式特征，随后训练该网络，与4.3中用MLP训练后的结果作对比。

可以看出浅层神经网络的分类效果较差，对于相对简单的分类任务都如此，可以想象到如果是真实案例的准确率会有多低。

欢迎大家关注公众号奇趣多多一起交流！

深度学习—从入门到放弃(一)pytorch基础
深度学习—从入门到放弃（二）简单线性神经网络