可解释的机器学习，用于科学的见解和发现（Explainable Machine Learning for Scientific Insights and Discoveries）

可解释的机器学习，用于科学的见解和发现（Explainable Machine Learning for Scientific Insights and Discoveries）

原文作者：Ribana Roscher, Bastian Bohn, Marco F. Duarte, and Jochen Garcke
翻译：Wendy

摘要（Abstract）

  机器学习方法在从数据中抽取重要的基础信息的广泛应用领域中已经取得了巨大成功。一项激动人心且相对较新的发展是自然科学中机器学习的普及，其主要目标是从观测或模拟数据中获得新颖的科学见解和发现。获得科学成果的先决条件是具有相关领域的知识，这是获得可解释性以及增强科学一致性所必需的。 在本文中，我们根据自然科学中的应用回顾了可解释的机器学习，并讨论了我们在这种情况下被认为相关的三个核心要素：透明性、可解读性和可解释性。 关于这些核心要素，我们提供了对结合了机器学习的最新科学著作的调查，尤其是在其各自的应用领域中使用了可解释的机器学习的方式。

1 引言（ Introduction）

  如今，尤其是随着深度神经网络（DNN）的兴起，机器学习方法已广泛用于商业应用中。这项成功使得机器学习（ML）在许多科学领域中的大量应用。通常，对这些模型进行高精度的训练，但是最近对理解特定模型的运行方式以及所做出决策的根本原因也有很高的要求。其背后的动机是，科学家们越来越多地采用ML来优化和产生科学成果，其中可解释性是确保其科学价值的前提。在这种情况下，已经出现了诸如可解释的人工智能（Samek等，2018），知情ML [von Rueden等，2019]或可理解的智力[Weld and Bansal，2018]等研究方向。 尽管相关，但概念，目标和动机却各不相同，并且核心技术术语以不同的方式定义。

  在自然科学中，利用ML的主要目标是科学理解，从观测数据推断因果关系，甚至获得新的科学见解。 使用ML方法，如今人们可以（半）自动处理和分析来自实验，观察或其他来源的大量科学数据。 具体目的和科学结果表示将取决于研究人员的意图，目的和目标，准确性的上下文标准以及预定的受众。 关于有足够的科学代表性的条件，我们指的是科学哲学[Frigg and Nguyen，2018]。

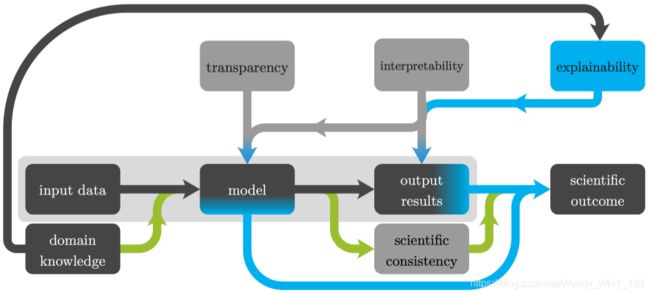
 图1：从中可以得出科学结果的主要基于ML的链：常用的基本ML链（浅灰色框）从给定的输入数据中学习黑匣子模型并提供输出。 给定黑匣子模型和输入输出关系，可以通过使用领域知识解释输出结果来得出科学结果。 另外，可以使用导致科学成果的领域知识来解释一个透明且可解读的模型。 此外，领域知识的纳入可以促进科学上一致的解决方案（绿色箭头）。

  本文提供了对旨在获得科学成果的最新机器学习方法的调查，在此我们专门关注自然科学。 有了科学的成果，就可以得出新颖的见解，有助于加深理解，或者可以揭示以前未知的科学发现。 从ML算法中获得科学见解和发现意味着从其输出和/或参数中收集有关数据背后的科学过程或实验的信息。

  应该注意的是，以数据为驱动的科学发现并不是什么新鲜事物，而是模仿了约翰内斯·开普勒和艾萨克·牛顿爵士的革命性工作，后者基于数据驱动和分析工作的结合。 如Brunton和Kutz [2019]所述，【数据科学并没有取代数学物理和工程学，而是在二十世纪扩大了它，导致的是复兴而不是革命。】新功能是将高质量数据与可伸缩的计算和数据处理基础结构相结合。

  该调查的主要贡献是讨论了导致基于科学成果的自然科学中常用的基于机器学习的链（见图1）。在本调查中透明，可解读性和可解释性这三个要素将发挥核心作用并将详细定义和讨论。核心是基本的ML链，从给定的输入数据中学习具有特定学习范式的模型，利用学习的模型产生输出结果。为了得出科学的结果，输出结果或模型是需要被解释的，其中可解读性是可解释性的前提。此外，解释模型需要透明性。另一个必不可少的部分是领域知识，它是实现可解释性所必需的，但也可以用于促进模型和结果的科学一致性。 通常，向算法提供领域知识意味着通过从领域洞察力（例如自然法则和化学，生物学或物理模型）中获得的信息来增强ML算法的输入数据，模型，优化器，输出结果或任何其他部分[ 冯·鲁登（von Rueden）等人，2019年]。 除了具有可解释性的目的之外，在没有足够数据的情况下，集成领域知识还有助于模型的可处理性和正则化。 也可能会提高模型的性能或减少计算时间。

  我们将从自然科学中为与这些主题相关的方法提供各种示例。 我们的目标是加深对应用于自然科学数据的ML算法的理解和更清晰的概述。

  在更广泛的上下文中，考虑ML算法的可解释性时可能涉及的其他属性是安全/信任，责任，重现性，可传递性，鲁棒性和多目标权衡或目标不匹配，请参见例如[Doshi-Velez and Kim，2017，Lipton，2018]。例如，在社会环境中，做出决定的原因通常很重要。典型的例子是（半）自动贷款申请，聘用决策或对保险申请人的风险评估，其中人们想知道模型为什么能给出特定的预测以及这些决策如何影响预测。在这种情况下，也是由于监管原因，一个目标是基于ML模型的决策涉及公平和道德的决策。在医学应用中，给出ML算法决策原因的重要性也很高，其中动机是提供对决策的信任，使患者对所做出的决策感到满意。这一切都受到《通用数据保护条例》的支持，其中包含有关使用个人信息的新规则。这些规则的一个组成部分可以用“解释权”来概括[Goodman and Flaxman，2017]。最后，对于部署用于决策支持和自动化的ML模型，尤其是在潜在变化的环境中，一个基本的假设是，如果模型可以解释，则可以更好地理解或更轻松地实现鲁棒性和可靠性[Lipton，2018]。

  本文的结构如下。 我们将在本文的第2节中讨论透明度，可解读性和可解释性。尽管这些术语更多地受方法论驱动，并涉及模型和算法的属性，但我们还描述了附加信息和领域知识的作用以及科学的一致性。在第3节中我们重点介绍了自然科学中的一些应用，这些应用使用这些概念可获得新的科学见解。

2 术语解读（Terminology）

  可以观察到，在有关可解释的ML的文献中，使用了几种具有不同含义的描述性术语，例如 Doshi-Velez和Kim [2017]，Gilpin等。 [2018]，Guidotti等。 [2018]，Lipton [2018]，Montavon等。 [2018]，默多克等人。 [2019]。 但是，可以识别出不同的想法。 出于这项工作的目的，我们区分了透明性，可解读性和可解释性。 粗略地说，透明度考虑的是ML方法，可解读性考虑的是ML模型和数据，而可解释性则考虑了模型，数据和人员参与。

透明性

  如果方法设计师可以描述和激励从训练数据中提取模型参数并从测试数据中生成标签的过程，那么ML方法就是透明的。 我们说ML方法的透明度关系到它的不同要素：这包括整体模型结构，各个模型组件，学习算法以及该算法如何获得特定的解决方案。本文在模型透明性，设计透明性和算法透明性之间进行区分。 通常，在所有方面都完全透明的ML方法值得怀疑。 通常会有不同程度的透明度。

  例如，考虑基于内核的ML方法[Hofmann等，2008； Rasmussen和Williams，2006]。所获得的模型是可访问且透明的，并且是内核函数的总和。各个设计组件是所选的内核。在线性或非线性内核之间进行选择通常是一个透明的设计决策。但是，基于欧氏距离的常用高斯核可能是非透明的设计决策。换句话说，可能不清楚为什么采用给定的非线性核。在这里，可以进行领域特定的设计选择，尤其是使用适当的距离度量来代替欧几里得距离，从而使该模型组件的设计变得更加透明。在高斯过程（GP）回归的情况下，可以使用最大似然框架将内核的特定选择构建到超参数的优化中[Rasmussen and Williams，2006]。从而，设计透明性超过了算法透明性。此外，从数学的角度来看，所获得的特定解是透明的。即，它是凸优化问题的唯一解决方案，可以重复获得它，从而实现算法透明性[Hofmann等，2008； Rasmussen和Williams，2006]。相反，特定解方法中的近似值，如提前停止，矩阵近似，随机梯度下降等，可能导致算法的（某些）不透明性。

  再举一个例子，考虑DNN [Goodfellow et al。，2016]。 该模型是透明的，因为它的输入-输出关系和结构可以用数学术语写下来。 基于领域知识选择的各个模型组件（例如DNN的一层）可以视为透明的设计。 但是，层参数（无论是其数量，大小还是所涉及的非线性）通常是临时性或启发式地选择的，并非出于知识的动机，因此这些决策在设计时并不透明。 学习算法通常是透明的，例如，可以容易地写下随机梯度下降。 但是，对诸如学习速率，批处理大小等其他超参数的选择具有更多的启发式，非透明算法性质。 由于存在多个局部最小值，因此该解决方案通常不容易重现； 因此，所获得的特定解决方案在算法上不是（完全）透明的。

  我们的观点与Lipton [2018]密切相关，他写道：“在非正式上，透明度与不透明度或“黑匣子”相反。 它意味着对模型工作机理的某种理解。 这里，在整个模型的级别（可模拟性），在各个组件（例如参数）的级别（可分解性）以及在训练算法的级别（算法透明性）都考虑透明度。”

  对ML算法的理解的重要贡献是它们的数学解释和推导，这有助于理解何时以及如何使用这些方法。 经典的例子是卡尔曼滤波器或主成分分析，其中每种都有几种数学推导，并增强了对它们的理解。 请注意，尽管有很多数学尝试可以更好地理解深度学习，但根据Charles [2018]，在这一阶段，“ DNN的[数学]解释似乎模仿了一种罗夏测验”。

  总的来说，我们认为三种形式的透明度在很大程度上不取决于具体数据，而仅取决于ML方法。 但是很明显，所获得的特定解，特别是（迭代）算法实现的“解路径”，取决于训练数据。 分析任务和属性类型通常在实现设计透明性中起作用。 此外，超参数的选择可能涉及模型结构，组件或算法，而在通过算法确定超参数时，特定的训练数据会再次发挥作用。

可解读性

  我们认为可解读性是关于使所获得的ML模型有意义。 通常，解读是指“解释的含义”或“以可理解的术语呈现” ； 另见Doshi-Velez和Kim，Gilpin等，Guidotti等的文章。 在解读的基础上，我们认为解释是一个单独的方面，在这里着重于第二个方面。 因此，可解读性的目的是以人类可以理解的方式呈现ML模型的某些属性。 理想情况下，可以回答Casert等人的问题。 [2019]：“我们能否理解ML算法基于其决策的依据？” 正式地，Montavon等。 [2018]状态：

• 解读是将抽象概念（例如预测类）映射到人类可以理解的领域中。

  可以通过可理解的代理模型获得解释，该代理模型类似于更复杂方法的预测[Gilpin等，2018； Guitotiti等，2018]。长期的方法涉及决策树、规则提取[Andrews等，1995]和线性模型。在原型选择中，选择一个或几个与检查的基准相似的示例，从中可以获得结果的标准。对于特征的重要性，采用线性模型中的权重来全局或局部地识别与预测相关的属性。例如，Ribeiro等 [2016]引入了模型不可知论方法LIME（局部可解读模型不可知论解释），该方法通过在基准附近创建局部线性代理模型来进行解释。灵敏度分析可用于检查模型输出（局部）如何取决于不同的输入参数[Saltelli等，2004]。从学习的模型的输入和输出中提取的信息也称为事后可解释性[Lipton，2018]或逆向工程[Guidotti et al。，2018]。进一步的细节，解释的类型和具体的实现可以在最近的研究中找到[Adadi和Berrada，2018； Gilpin等，2018； Guitotiti等，2018]。

  显着性蒙版或热图之类的视觉方法会根据特征重要性或敏感度分析在输入中显示相关模式，以解释模型决策，特别是用于图像分类的深度学习方法时[Hohman等，2018； Montavon等，2018 ，Olah等人，2018年]。 请注意，最近引入了一种用于解释神经网络的正式且严格的概念：

• 如果在对其余特征进行随机化时预期分类器分数几乎保持不变，则认为一组输入特征与分类决策相关

[MacDonald等，2019]。 作者证明，在这种概念下，即使考虑任何非平凡因素内的近似值，也很难找到相关特征的小集合。 这一方面显示了算法确定解释的难度，另一方面证明了启发式方法在实际应用中的当前使用是正确的。

  在无监督学习中，分析目标可以是更好地理解数据。 例如，通过线性或非线性降维[Lee and Verleysen，2007，Cichocki et al。，2009]或通过检查低秩张量分解的成分[Mørup，2011]来解释获得的表示。

  请注意，与透明度相反，要始终获得数据的可解读性。 尽管存在与模型不可知的可解读性方法，但是透明性或保留模型可以帮助解读。 此外，特定的方法取决于透明度，例如，DNN的分层相关传播利用已知的模型布局[Montavon等人，2018]。

  尽管解读性方法允许检查单个数据，但Lapuschkin等人。 [2019]观察到，解读大量的个体非常耗时。 作为自动处理单个基准的单个解释的步骤，他们采用了许多数据的热图聚类来获得对ML算法的预测的解释的总体印象。

  最后，请注意，对ML方法性能的可解读性和人为理解最后可能会导致选择不同的ML模型、算法或数据预处理方法。

可解释性

  尽管人们对可解释性机器学习的研究被广泛认为是重要的，但对可解释性概念的共同理解仍需要发展。 关于解释，也有人认为机器学习与所谓的解释科学（例如法律，认知科学，哲学和社会科学）之间还是有一定的期望差距[Mittelstadt等，2019]。

  尽管哲学和心理学方面的解释长期以来一直是人们关注的焦点，但没有一个简洁的定义。 例如，解释的完整性或因果程度可能会有所不同。 我们建议遵循最近的评论中的模型，该评论将社会科学的见解与AI中的解释联系起来[Miller，2019]，该模型将解释性问题分为三类：（1）什么？问题，例如“发生了什么事件？”; （2）如何进行的问题，例如“该事件是如何发生的？”； （3）为什么-问题，例如“为什么发生此事件？”。 从可解释的AI领域中，我们考虑了Montavon等人的定义。 [2018]：

• 一种解释是可解释域的特征的集合，这些特征为给定示例做出了决策（例如分类或回归）做出了贡献。

如Guidotti等人所写。 [2018]，“ [在可解释的ML中，这些定义隐含地假设构成解释的可理解术语中表达的概念是独立的，不需要进一步的解释。”

  另一方面，我们认为，解释的集合只能是来自领域知识且与分析目标有关的其他上下文信息的解释。 换句话说，可解释性通常不能纯粹通过算法实现。 就模型而言，以人类可以理解的方式来解释单个数据可能无法提供理解决策的解释。 例如，对于几个数据而言，最相关的变量可能是相同的，但对于理解整体预测行为的重要观察可能是，在对解释的排名中，为每个数据确定了不同变量的关联列表。 总体而言，结果将取决于基础分析目标。 “为什么要做出决定？” 将需要不同的解释，而不是“为什么决定基准A与（附近的）基准B不同？”。

  换句话说，出于可解释性，机器学习“用户”的目标非常重要。 根据阿达迪（Adadi）和贝拉达（Berrada）[2018]的说法，基本上有四个理由寻求解释：证明决策合理性，（加强）控制，改进模型以及发现新知识。 出于监管目的，可能需要通过示例或（局部）特征分析进行解释，以便可以检查某些“正式”方面。 但是，要获得ML的科学成果，就需要一种理解。 在这里，科学家正在使用数据，方法的透明性及其解释来使用领域知识来解释输出结果（或数据），从而获得科学的结果。

  此外，我们建议区分算法的解释和科学的解释。 通过算法的解释，旨在揭示导致机器学习方法决策的根本原因，这就是可解释的机器学习旨在解决的问题。 为了进行科学的解释，Overton [2013]确定了五种类别，以对科学中解释的绝大多数对象进行分类：数据，实体，种类，模型和理论。 此外，可以观察到，对于科学解释是否有统一的一般解释仍然是一个悬而未决的问题。

  还应注意，可以使用解释来操纵。为了说明起见，Baumeister和Newman [1994]区分了寻求做出最准确或最佳决策的直觉科学家和希望证明预选结论合理的直觉律师。考虑到这一点，人们经常希望以人为中心来解释黑匣子模型。有简单或纯算法的解释，例如基于强调图像中的相关像素。在所谓的缓慢判断任务中，解释可能更容易引起确认偏见。例如，使用以人为中心的解释作为评估基准可能会偏向某些个人。此外，对要求人们产生解释或想象情景的实验操作的研究的回顾表明，人们被要求对某种可能性表达更大的信心，尽管是错误的，但当被要求为它解释或想象这种可能性时[Koehler，1991]。

领域知识

  如前所述，领域知识是可解释性的重要组成部分，但对于处理小数据方案或出于性能原因，也是如此。 von Rueden等人提出了一种将知识显式集成到ML管道中的分类法，即所谓的知情ML。 [2019]。 涉及三个方面：

1. 知识类型
2. 知识的表示和转化
3. 将知识整合到ML方法中。

另请参见Karpatne等的相关著作。 [2017]，他们使用了术语“理论指导的数据科学”或“ Raissi等人，2017a”的物理信息学习方法。 为了本文的目的，我们遵循von Rueden等人的观点。 [2019]，旨在按照科学的形式，从科学，过（工程或生产）流程到世界知识以及最终的个人（专家）直觉安排不同类型的知识。 可以将知识分配给此不完整列表中的几种类型当中去。

  在科学中，知识通常以数学方程式（例如解析表达式或微分方程式）的形式给出，作为实例和/或类之间以规则或约束形式的关系。 它可以以本体形式，对称性或使用相似性度量来表示。 知识可以通过模型的数值模拟或通过人类交互来转化。

  作为ML方法的组成部分，我们需要考虑训练数据，假设空间，训练算法和最终模型。 在每一种情况下，都可以结合其他知识。 特征工程是将知识整合到训练数据中的一种常见且长期的方式，而使用数值模拟来生成（附加）训练数据是一种现代现象。

  通过选择模型的结构，可以将知识整合到假设空间中。 例如，通过定义神经网络的特定体系结构，或通过选择观察变量之间存在或不存在的联系的概率分布结构。 训练阶段的一个示例是根据附加知识，例如通过添加一致性项来修改损失函数。 最后，可以例如通过检查预测的已知约束来将获得的模型与现有知识相关联。 这方面我们称为科学一致性，并认为获得科学成果特别重要。

科学一致性

  为科学应用生成可靠结果的基本前提是科学一致性。这意味着所获得的结果是合理的，并且与现有的科学原理相一致。在领域知识的基础上选择和制定要满足的科学原理，在这种情况下，整合的方式是知情ML等领域的核心研究问题。在图1的链中，可以通过分析输出结果在模型设计阶段或后验中将科学一致性视为先验。冯·鲁登（von Rueden）等人指出。 [2019]，设计阶段的科学一致性可以理解为正则化效应的结果，其中存在各种方式来将解决方案空间限制为科学上一致的解决方案。 Reichstein等。 [2019]将可解释性之外的科学一致性确定为成功地在地球科学中采用深度学习方法需要解决的五个主要挑战之一。 Karpatne等。 [2017]通过将一致性定义为衡量绩效的重要组成部分来强调一致性的重要性：

• [理论指导的数据科学]的总体愿景之一是将[…]一致性作为模型性能的关键组成部分以及训练的准确性和模型的复杂性。可以通过以下模型性能的修订目标以简单的方式来总结：性能∝准确性+简洁性+一致性。

他们讨论了几种将解决方案空间限制为物理上一致的解决方案的方法，例如，通过（1）设计模型家族（例如特定的网络体系结构），（2）使用例如特定的初始化，约束或（ 损失）正则化；（3）模型输出的完善（例如，使用闭式方程式或模型仿真）；（4）理论和ML的混合模型；以及（5）使用真实数据（例如数据同化）增强基于理论的模型 或校准。

  总体而言，将解决方案空间明确限制为科学上一致的解决方案并不是实现有价值的科学成果的必要条件。 但是，忽略此限制意味着即使从数学角度已获得最佳结果，也无法保证一致的解决方案。

3 机器学习的科学成果（ Scientific Outcomes From Machine Learning）

  在本节中，我们将回顾几个使用ML的示例，并努力提高透明度，可解读性和可解释性的不同水平，以产生科学的结果。 我们将重点介绍利用自然科学中广泛的科学领域知识的示例。

  我们定义了两大类：第一类是通过解释输出结果来推导科学结果。 许多工作通过学习ML模型并从已知的投入产出关系到新的投入产出对进行概括，从而解决了科学成果的推导问题。 到目前为止，大多数方法仅从科学的角度（科学解释）解释结果是什么，但不能从算法的角度（算法解释）回答为什么得出这种特定结果的问题。 其他方法尝试根据特定的对应输入科学地解释输出。 在这里，使用了解释工具，其中该模型仅用作最终解释结果的一种手段，并且自身并未明确分析。 这表明最低程度的可解读性，而无需透明或可解读的模型。

  另一种方法是通过解释模型得出科学结果。 在此，使用解释工具将模型中的过程投影到可解释的空间中，然后可以利用领域知识对其进行解释。 科学解释和算法解释都可用于得出科学结果。 这意味着，即使科学结果由领域专家更明确地定义，模型的透明性和可解释性也不是这些方法的前提。 请注意，以下研究作品集是最近文献的非详尽选择，我们旨在覆盖具有各种科学成果的ML的广泛使用。

3.1 通过解释输出结果得出科学结果（Scientific Outcomes by Explaining Output Results）

3.1.1 直观的科学结果的预测（Prediction of Intuitive Scientific Outcomes）

  本小节中描述的工作是在物理领域进行的，通常会得出两种结果。 首先是直观物理学的衍生：日常观察的自然法则，即使在人类没有受到相对训练的情况下，例如，塔是否会倒塌，也可以帮助我们预测事件的结果[McCloskey，1983]。 另一个与特定物理参数的估计有关，从中可以得出静态属性或对象行为。 Chang等。 [2017]分别将这些方法表示为自下而上，其中观察值直接映射到对某些对象行为或场景的物理结果的估计，并表示为自上而下，其中推断参数以解释场景。 在这两种情况下，都只寻求科学的解释。

  通常要考虑的任务是预测某个结构在图像或视频中是否崩溃。 Lerer等。 [2016]和Li等。 [2016]使用视频模拟学习直观的物理知识，例如关于木块塔的稳定性。 Lerer等。 [2016]使用ResNet-34 [He等人，2016]和Googlenet [Szegedy等人，2015]预测木块塔的倒塌，以及DeepMask [Pinheiro等人，2015]和自定义名为PhysNet的网络可预测塔楼倒塌时木块的轨迹。第一个任务被表述为二进制分类任务，第二个任务被表述为语义分割，其中每个木块都被定义为一个类。在这两项任务中，PhysNet在合成数据上的表现均优于人类受试者，并在真实数据上取得可比的结果。在选择网络层的意义上，使PhysNet的设计透明化，以便在粗略分析其固有物理特性之前，通过局部和平移不变的图像放大来确定木块的排列。通过对遮挡图像的实验，作者能够通过进行热图分析来获得二元分类任务的可解释性。 Li等人对更复杂的场景或形状不同的物体进行了类似的实验。 [2016]和Groth等人。 [2018]使用各种流行的卷积神经网络（CNN）。尽管通用的CNN选择本身似乎并不透明，但Groth等人。 [2018]通过训练他们的算法以通过将新物体放置在不稳定的堆栈顶部来主动抵消不稳定性，从而向可解释且具有物理意识的模型迈出了第一步。汤普森（Tompson）等。 [2017]和Jeong等。 [2015]使用类似的方法来应用，例如基于不可压缩的Navier-Stokes方程的流体模拟，其中引入了基于物理的损耗以实现合理的结果。在汤普森等人的想法。 [2017]将使用透明的成本函数设计，方法是在每个时间步长将无散度场条件重新设置为无监督学习问题。 Jeong等人使用的随机森林模型。 [2015]预测流体粒子的速度由于其简单性而被视为一种透明的选择。

3.1.2 科学参数和性质的预测（Prediction of Scientific Parameters and Properties）

  尽管刚刚描述的方法将科学结果预测设置为监督学习问题，但是常见的监督任务（例如，分类，对象检测和预测）与对场景及其推理的实际理解之间仍然存在差距。迄今为止，所提供的方法还没有学习能够捕获和推导对象及其周围环境之间相互作用的物理特性和动力学的模型。因此，该模型无法固有地解释为什么从科学的角度获得一些特定的结果。 已经有了一些分类和回归框架来应对这一挑战。

  例如，Stewart和Ermon [2017]以一种无监督的方式检测和跟踪视频中的对象。为此，他们使用了回归CNN并引入了与物理法则相比可以衡量输出一致性的术语，而物理法则可以专门并彻底地描述视频中的动态。在这种情况下，回归网络的输入是视频序列，输出是物理参数的时间序列，例如抛出物体的高度。通过将领域知识和图像属性整合到它们的损失函数中，它们的设计过程变得可解读，并且由于与底层物理过程进行了比较，因此获得了可解释性。但是，由于采用了带有ADAM最小化器的标准CNN，因此模型和算法并不完全透明。Wu等。 [2016]引入了Physics101，一个包含17000多个视频剪辑的数据集，其中包含101个具有不同特征的对象，这些数据片段是为导出速度和质量等物理参数而构建的。在他们的工作中，他们使用LeNet CNN架构[LeCun et al，1998]捕获视觉和物理特征，同时基于材料和体积明确整合物理定律，以实现科学一致性。 他们的实验表明，可以使用估计的物理特性对物体跌倒或碰撞后的行为进行预测，这些特性可以作为独立物理模拟模型的输入。Monszpart等。 [2016]引入了SMASH，SMASH从碰撞对象的视频中提取物理碰撞参数，例如碰撞前和碰撞后的速度，并将其用作现有物理引擎进行修改的输入。 为此，他们遵循动量守恒等物理定律，使用约束最小二乘估计来估计视频中对象的位置和方向。 基于确定的轨迹，可以导出诸如速度之类的参数。 尽管他们的方法更多地基于统计参数估计而不是机器学习，但他们的模型和算法构建过程是完全透明和可解读的。由于计算与基本物理定律的直接关系，单个结果变得可以解释。

  其他学科也使用ML来帮助指导新的科学见解和发现。特别是，通常用回归算法来解释一些物理现象。Mauro等。 [2016]提出了一种新功能玻璃的设计方法，该方法包括预测与玻璃制造和最终使用特性相关的特性。除其他外，他们利用神经网络来估计包含多达8种不同组分的各种硅酸盐组合物的液相线温度。为此，他们从具有已知输出特性的数百种复合材料中学习，并将模型应用于新颖的未知复合材料。通常，确定产生合适液相线温度的硅酸盐的最佳组成是一项昂贵的工作，并且通常基于反复试验。虽然在基于最小二乘损失的神经网络训练过程中缺乏透明度或可解读性以了解相应的液相线温度，但作者还针对不同的兴趣量引入了更多的物理驱动模型，还需要对这些模型进行估计。最终有助于功能眼镜的设计过程。

  对于有机光伏材料，[Pyzer-Knapp等，2016； Lopez等，2017]提出了一种利用量子化学计算和ML技术将理论结果校准为实验数据的相关方法。作者将已经进行的现有实验视为当前知识，并将其嵌入概率非参数映射中。特别地，使用高斯过程来学习通过计算模型从实验类似物中计算出的特性偏差。通过使用化学的Tanimoto相似性度量并基于实验观察结果建立先验，可以实现模型的透明性和可解释性。此外，由于预测结果涉及返回的每个校准点的一致性，因此，当该方案用于不适合该方案的系统时，用户会被提前告知不适用[Pyzer-Knapp等，2016]。在洛佩兹（Lopez）等人中，[2017]，由于目前可能有效地筛选了超过51,000个分子，因此已在探索的分子空间内鉴定出838个高性能候选分子。

  在凌等人。 [2016b]，提出了一种用于 雷诺平均Navier-Stokes（RANS）湍流建模的深度学习方法。在这里，领域知识导致了网络架构的构建，该网络架构使用高阶乘法层来嵌入不变性。与通用的、难以解释的神经网络体系结构相比，该研究表明具有明显更准确的预测。此外，对于具有比任何训练案例不同的几何形状的测试案例的改进预测表明，对于不仅仅是插值情况的改进RANS预测似乎是可以实现的。 Wang等人提出了一种用于 高速平板湍流边界层的RANS模型雷诺应力 的相关方法。 [2019]，它使用了Ling等人提出的具有基本张量不变性的系统方法。 [2016a]。 另外，采用了一种预测信心度量和非线性降维技术来提供对预测信心的先验评估。

  在Raissi等人中。 [2017b]，提出了一种从噪声数据中学习通用参数线性微分方程系数的数据驱动算法，从而解决了所谓的逆问题。该方法采用了高斯过程先验，它适合于相应的已知类型的差分算子。因此，将通用的ML模型与领域知识以基础差分方程的结构形式结合起来，可得出一种有效的方法。除了具有不同属性的经典基准问题外，该方法还用于功能基因组学的示例应用程序，基于实际表达数据确定遗传网络的结构和动力学。 Hoerig等人提出了一种相关的基于信息的机器学习方法来解决生物力学应用中的逆问题。 [2017]。在此，在准静态载荷下对软生物介质进行机械性能成像时，将从估计的应力和应变中计算出弹性成像参数。 Camps-Valls等人研究了遥感中具有物理意识的GP模型。 [2018]。尤其是，在根据实际原位数据进行逆向建模时，使用了包含普通差分方程的潜能模型。学习到的潜在表示形式允许根据产生输入输出观察关系的物理机制进行解释，即一个潜在函数捕获了输出的平滑和周期性成分，而另外两个集中于具有重要残留周期性成分的噪声部分。

  在Eigel等人中可以找到基于张量的ML来解决不确定性量化问题。 [2018]。在此，基于几个样本学习了参数对流扩散偏微分方程的解。该方法不是直接针对可解读性或可解释性，而是通过从PDE的解决方案空间中计算出物理上相关的感兴趣量，来帮助加快获得科学见解的过程。 Raissi [2018]提出了一种非线性回归方法，该方法使用DNN来从时空收集的分散数据中学习偏微分方程的闭合形式表示，从而发现动态依存关系，并获得可随后用于预测未来状态的模型。在包括Burgers方程，非线性Schr？odinger方程或Navier-Stokes方程在内的基准研究中，从数值模拟数据直到特定时间都可以了解基本动力学。所获得的模型用于预测未来状态，其中观察到的相对L2误差高达10-3数量级。虽然该方法固有地对PDE和动力学本身进行建模，但是一般通用的神经网络模型不允许对基础过程的结构得出直接的科学结论。

  Mottaghi等。 [2016]引入牛顿神经网络，以便从单个彩色图像中预测对象的长期运动。他们没有从图像中预测物理参数，而是引入了12个作为物理抽象的牛顿场景，其中每个场景都由定义动力学的物理参数定义。在这些场景之一中，包含感兴趣对象的图像被映射到一个状态，该状态最能描述图像中的当前动态。牛顿神经网络是两个并行的CNN，其中一个对图像进行编码，而另一个则从通过游戏引擎模拟12种牛顿场景的视频获取的卷积滤波器中得出。最终，两个CNN的特定耦合导致了一种可解释的方法，该方法也（部分地）允许解释单个输入图像的分类结果。朱等。 [2015]引入了一个框架，该框架从色深视频中计算物理概念，这些视频解释了工具和工具的使用，例如开裂螺母。在他们的工作中，他们学习每种工具和任务组合的面向任务的表示形式，这些组合是在具有空间，时间和因果关系的图形上定义的。他们区分了13个物理概念（例如，粉刷墙壁），并表明该框架能够通过选择适当的工具和工具用途来从已知到看不见的概念进行概括。他们透明的类似于SVM的学习过程允许使用相当小的样本集。

3.1.3 3.1.3科学成果的解释工具（Interpretation Tools for Scientific Outcomes）

  其他方法使用解释工具从学习的模型中提取信息，并帮助科学地解释单个输出或联合多个输出。 通常，采用直接方法通过可视化学习的表示形式，自然语言表示形式或示例讨论来呈现此信息。 尽管如此，仍然需要人工交互来解释此附加信息，该附加信息必须在事后分析过程中从学习的模型中得出。

  Kailkhura等。 [2019]讨论了用于材料科学领域的科学发现的可解释的机器学习。他们确定了将ML用于材料科学应用程序时的挑战，例如可靠性-解释性权衡。他们指出，许多著作将可解释性和可解释性视为复杂性的反面，从而在降低复杂性时会提高准确性和可靠性。在最坏的情况下，这可能会导致误解或错误的解释。在他们的工作中，他们提出了一组简单的模型来预测材料特性，并提出了一种新颖的评估指标，该指标通过量化泛化性能来关注信任。此外，他们的管道还包含一个原理生成器，该生成器为单个预测提供决策级解释，并为整个回归模型提供模型级解释。详细地讲，它们根据专家分析和解释的原型产生解释，并通过估计材料子类的特征重要性产生全局解释。

  Kailkhura等。 [2019]讨论了用于材料科学领域的科学发现的可解释的机器学习。他们确定了将ML用于材料科学应用程序时的挑战，例如可靠性-解释性权衡。他们指出，许多著作将可解读性和可解释性视为复杂性的反面，从而在降低复杂性时会提高准确性和可靠性。在最坏的情况下，这可能会导致误解或错误的解释。在他们的工作中，他们 提出了一组简单的模型来预测材料特性，并提出了一种新颖的评估指标，该指标通过量化泛化性能来关注信任。此外，他们的模型还包含一个原理生成器，该生成器为单个预测提供决策级解释，并为整个回归模型提供模型级解释。详细地讲，它们根据专家分析和解释的原型产生解释，并通过估计材料子类的特征重要性产生全局解释。

  在许多领域中，可以观察到对使用自动方法来估计特征重要性的兴趣增加。 手工制作和手动选择的特征通常更容易理解，而自动确定的特征可以揭示以前未知的科学属性和结构。例如， 金斯堡（Ginsburg）等人。 [2016]提出了FINE（在非线性嵌入中的功能重要性）来分析ER +乳腺癌组织玻片中的癌症模式。 该方法通过估计原始特征对降维歧管的相对贡献，将原始特征和自动衍生的特征彼此关联。 该过程可以与各种可能不透明的非线性降维技术相结合。 由于特征贡献检测，所得方案仍然是可解读的。

  可以说，可视化是使用最广泛的解释工具之一。 Hohman等 [2018]对深度学习研究中的视觉分析进行了调查，其中开发了这种可视化系统来支持模型解释，解读，调试和改进。这些分析的主要使用者是模型开发人员和用户以及非专家。Ghosal等。 [2018]使用解释工具进行基于图像的植物胁迫表型分析。他们训练了CNN模型，并在各个层中确定了最重要的特征图，这些图将压力和疾病症状的视觉线索隔离开来。它们生成所谓的解释图，作为由其激活级别指示的最重要特征图的总和。专家对手动标记的视觉提示与自动得出的说明图的比较表明，自动标记和手动标记之间具有很高的一致性。他们方法的目标是分析其模型的性能，提供可人工解释的视觉提示以支持系统的预测，并提供用于识别植物胁迫的重要提示。Abbasi-Asl等。 [2018]引入了DeepTune，它是CNN的稳定驱动的可视化框架，适用于神经科学。 DeepTune由一系列CNN组成，它们可以学习自然图像的多种互补表示。这些CNN的特征被输入到回归模型中，以预测视觉皮层中神经元的放电率是V4。特征提取和回归模块的组合可以准确预测V4神经元对其他视觉刺激的反应。然后可以通过梯度优化从受过训练的模块中生成每个神经元的代表性视觉刺激。作为另一个示例，ML已应用于功能磁共振成像数据，以设计可预测精神疾病的生物标记。但是，只有“替代”标签可用，例如行为评分，因此生物标记本身也是最佳描述符的“替代” [Pinho等人，2018； Varoquaux等人，2018]。生物标志物设计促进了空间紧凑的像素选择，产生了用于疾病预测的生物标志物，这些生物标志物集中在大脑区域。然后由专家医师考虑这些。由于分析基于高维线性回归方法，因此可以确保ML模型的透明度。

  可解释性方法也已用于利用时间序列数据的应用程序，通常是通过突出显示序列数据的特征来实现的。例如，Deming等。 [2016]通过在基因组序列上训练的神经网络中应用注意模块，通过可视化注意mask weights来识别重要的序列基序。在这里，他们提出了一个遗传架构，该架构通过迭代搜索各种神经网络构造块来找到合适的网络架构。 他们特别指出，神经网络体系结构的选择在很大程度上取决于应用领域，如果没有关于网络设计的现有知识，这将是一个挑战。 请注意，根据优化的架构，注意力模块和专家知识可能会导致不同的科学见解。

  此外，辛格等。 [2017]在AttentiveChrome神经网络中将注意力模块用于基因组学。 该网络包含关注模块的层次结构，以获取有关网络关注的重点和目的的见解，从而获得结果的可解释性。 崔等人 [2016]在医疗保健中开发了一种基于层次注意力的解释工具，称为RETAIN（逆时针注意力）。 该工具从患者的病史中识别出患者的过往访视以及这些访视期间的重要临床变量，以支持医学解释。 Chen等人已在递归神经网络中使用注意力模块进行基于多模式传感器的活动识别。根据活动的不同，他们的方法会为网络的决策提供最有帮助的身体部位，模态和传感器。

  在某些情况下，可以通过将模型用作基础设计问题的驱动器来解释模型。 例如，Brookes和Listgarten [2018]提出了一种以数据为中心的科学设计方法，该方法基于考虑的数据的生成模型（例如基因组或蛋白质）和目标数量或属性的预测模型（例如 ，疾病指标或蛋白质荧光。 对于DNA序列设计，通过将预测模型应用于生成模型的样本来整合这两个组件。 这样一来，就可以通过在生成模型上利用自适应采样技术来生成新的合成数据样本，以优化数量或属性的值。

  尽管如此，诸如混淆矩阵之类的经典工具也被用作解释科学结果途中的工具。 在生物声学应用中，使用声学传感器识别无核生物，Colonna等人。 [2018]使用分层方法在三个分类级别上进行共同分类，即家庭，属和物种。 研究每个级别的混淆矩阵，例如可以识别不同物种之间的生物声相似性。

3.2 通过解释模型得出的科学结果（Scientific Outcomes by Explaining Models）

  
1148/5000
到目前为止，提出的方法要么将模型视为黑匣子，要么仅通过应用解释工具更好地解释输出结果而间接使用它。 Liao和Poggio [2017]提出了一个名为“面向对象的深度学习”的概念，其目的是将DNN转换为符号描述，从而获得可解读性和可解释性。他们指出，在DNN中，通常天生就没有诸如对象或事件之类的符号概念的显式表示，而是面向特征的表示，这很难解释。 在对象的表示中，可以将对象构造为具有可解读和可解释的属性。 尽管到目前为止尚不常用，但是他们的工作为提高模型的可解释性指明了一个有希望的方向。 本节中回顾的方法使用面向特征的通用表示形式，着重于系统中变化的潜在因素的解读，这可以由专家随后进行解释。 我们将进一步关注最近的ML方法，该方法关注于模型的单个组件或整个模型结构的解释和说明。

  与第3.1节中的大多数工作依赖于相关参数的先验知识相反，其他一些工作则得出了环境的特征，而没有对基础科学过程的任何假设。 例如，Ehrhardt等。 [2017]推导物理参数时，无需假设有关物理过程的先验知识，也无需对基础物理模型进行建模，以便随时间推移在简单物理场景中进行预测。 在这里，物理上可解释的参数不仅作为结果导出，而且还集成在循环的端到端长期预测网络中。 因此，不需要仿真软件和基本物理定律的显式建模。

  另一个广泛的框架[Yair等，2017； Dsilva等，2018； Holiday等，2019]利用无监督学习方法来学习物理过程观测值的低复杂度表示。 在许多情况下，基础过程的自由度较小，这表明非线性流形学习算法能够将这些自由度识别为低维非线性流形嵌入的组件维，从而保留了原始数据空间基础几何的自由度。

  Iten等。 [2018]引入了SciNet，一种改进的变分自动编码器，它从实验数据中学习表示形式，并使用学到的表示形式从中获取物理概念，而不是从实验输入数据中得出物理概念。学习的表示被迫比实验数据简单得多，并且包含系统的解释因素，例如物理参数。这通过以下事实证明：物理参数和隐藏层中神经元的激活具有线性关系。此外，Ye等。 [2018]在他们的神经网络中构建瓶颈层来表示物理参数，以预测视频中对象碰撞的结果。但是，并不是学习瓶颈层的体系结构，而是使用有关底层物理过程的先验知识进行设计的。丹尼尔斯等。 [2019]使用他们的机器学习算法“ Sir Isaac” [Daniels and Nemenman，2015]推断生物时间序列数据的动力学模型，以了解和预测蠕虫行为的动力学。他们为微分方程系统建模，其中隐藏变量的数量由系统自动确定，其含义可以由专家解释。

  最近已经探索了使用嵌入式方法的特征选择方案来建立或优化物理过程[Rudy等，2017]和材料科学[Ghiringhelli等，2017，Ouyang等，2018]中的模型。他们使用稀疏性惩罚，提出了可以解释感兴趣属性的变量组，并提出了最简单的模型，即在达到目标准确度的情况下涉及尽可能少的变量的模型。 Meila等。 [2018]提出了一种稀疏性增强技术，以恢复从无监督的非线性降维方法获得的嵌入坐标的域特定含义。 作为一个说明性的例子，研究了乙醇分子，该方法确定了键扭，该键扭解释了从嵌入方法获得的环面，该环面反映了两个旋转自由度。 稀疏性的应用在利用偏微分方程和动力学系统模型的更广泛的问题类别中也被证明是卓有成效的[Tran and Ward，2017； Mangan等，2016； Schae ff er等，2013]。

  例如，可以为特定的科学应用定制复杂的ML方法（例如DNN），以便所使用的体系结构限制或提升网络建模数据中所需的属性。例如，在用于反演的等离子物理建模中，可以通过修改后的深度学习网络来促进诸如正性和平滑度之类的属性[Matos等，2018]。同样，污染物在土壤中的分散特性可以通过长期短期记忆网络成功建模[Breen et al，2018]。在[Adiga et al，2018]中，ML在流行病学中的应用利用了网络动态系统模型来进行传染动态，其中节点对应于具有指定状态的对象；因此，ML模型的大多数属性与所考虑的科学领域的属性相匹配。 Ma等。 [2018]引入了 可见的神经网络，该网络将基因本体树的层次结构编码为NN， 无论是从文献中还是从大规模分子数据集推论而来。这使得能够进行透明的生物学解释，同时成功预测基因突变对细胞增殖的影响。此外，有人认为所采用的 深层次结构在多个尺度上捕获了许多不同的特征簇，并将解释从模型输入推到了代表生物子系统的内部特征。 在他们的工作中，尽管在模型训练期间没有提供有关子系统状态的任何信息，但是以前未记录的学习的子系统状态可以通过分子测量来确定。

  理解诸如群体，关系和互动等结构是实现科学成果的主要目标之一。但是，它提出了一个核心挑战，到目前为止，在这一领域仅进行了有限的工作。例如，严等[2019]在名为GroupINN的可解释神经网络中引入了一个分组层，以识别端到端模型中的神经元子组。在他们的工作中，他们建立了一个网络，用于分析以功能图表示的大脑功能性磁共振图像的时间序列，目的是揭示高度预测性的大脑区域与认知功能之间的关系。他们没有使用整个功能图，而是利用网络中的分组层来识别神经元组，其中每个神经元代表图中的一个节点，并对应于大脑中感兴趣的物理区域。粗化图中的分组节点被分配到感兴趣的区域，这对于预测认知功能很有用，并且组之间的连接定义为功能连接。

  Tsang等。 [2018]引入了神经交互检测，这是一种用于检测统计交互的前馈神经网络。 通过检查学习到的隐藏单元的权重矩阵，他们的框架能够分析希格斯-玻色子数据集中的特征相互作用[Adam-Bourdarios等，2014]。 具体来说，他们分析了模拟粒子环境中的特征相互作用，这些相互作用是由希格斯玻色子的衰变引起的。 舒特等人使用了深张量网络。 [2017]在量子化学中预测分子能量直至化学准确性，同时允许进行解释。 所谓的局部化学势，是一种灵敏度分析的变体，其中一种测量在给定位置插入电荷的神经网络输出上的影响，可以用来从学习的模型中获得更多的化学见解。 例如，可以从这些三维响应图确定芳香环在稳定性方面的分类。

  Lusch等。 [2018]构建了一个DNN，用于根据数据计算Koopman特征函数。在领域知识的激励下，他们采用辅助网络对连续频率进行参数化。由此，获得了紧凑的自动编码器模型，该模型另外是可解读的。对于非线性摆的例子，可以将通过深层神经网络学习到的两个本征函数映射为幅度和相位坐标。以这种可解释的形式，可以观察到幅度跟踪了哈密顿能的能级集，这一新见解与作者先前未知的最新理论推导是一致的。在单细胞基因组学中，采用计算数据驱动的分析方法来揭示细胞身份的多种同时性，包括发育轨迹，细胞周期或空间背景下的特定状态。分析的目的是获得细胞经历的动态转变的可解释的表示，该动态转变可以确定细胞组织和功能的不同方面。在这里，重点是 从单细胞型蛋白质到聚类细胞的无监督学习方法，从而系统地预先检测未知的细胞亚型，然后在第二步中研究定义标记， 参见[Wagner et al，2016]。审查本应用程序领域中的关键问题，进展和未解决的挑战。

自然科学中有关机器学习的相关调查（Related Surveys about Machine Learning in the Natural Sciences）

  巴特勒等。 [2018]概述了将ML用于分子和材料科学的最新研究。 假设标准的ML模型是数值的，则算法需要合适的数值表示形式来捕获相关的化学性质，例如库仑矩阵和分子图，以及代表晶体结构的径向分布函数。 监督学习系统通常用于预测化合物和材料的数值特性。 无监督学习和生成模型正用于指导化学合成和化合物发现过程，其中成功地采用了深度学习算法和生成对抗网络。 利用有机化学和语言学之间相似性的替代模型基于化合物的文本表示。

  如Ching等人（2003年）所述，在生物学和医学中已经使用了几种机器学习方法来获得新的见解。 [2018]适用于广泛的深度学习方法类。监督学习主要集中于疾病和疾病类型的分类，患者分类以及药物相互作用的预测。无监督学习已应用于药物发现。作者指出，除了推导新发现外，对这些发现的解释也非常重要。此外，对于大型训练数据集的深度学习需求，限制了其当前的适用性，超出了成像（通过数据增强）和所谓的“组学”研究。 Gazestani和Lewis [2019]概述了系统生物学中的深度学习方法。他们描述了如何设计DNN，这些DNN对通过组合各种数据类型而生成的广泛的现有网络和系统级知识进行编码。据说，这样的设计可以在生物系统中的层次交互作用方面为模型提供信息，这对于做出准确的预测很重要，但在输入数据中不可用。

  Reichstein等。 [2019]概述了地球系统科学中的机器学习研究。 他们得出结论，虽然探索，假设生成和检验的总体周期保持不变，但现代数据驱动的科学和机器学习可以提取观测数据中的模式，以挑战复杂的理论和地球系统模型，从而强有力地补充和丰富了地球科学研究。 同样 Karpatne等[2018]指出，有必要与地球科学领域的领域专家和ML研究人员密切合作，以解决新颖而相关的任务。 他们指出，开发可解释和透明的方法是理解数据中的模式和结构并将其转化为科学价值的主要目标之一。

致谢（Acknowledgements）

  部分工作是在美国加利福尼亚大学洛杉矶分校的纯粹与应用数学研究所举办的“极限尺度的科学：大数据与大规模计算相结合的地方”长期计划中完成的。 我们感谢他们在计划期间提供的财务支持。 我们衷心感谢长期计划的参与者进行了富有成果的讨论，特别是陶凯敬，高龙飞，彼得罗·格兰迪内蒂，菲利普·海内尔，莫伊塔巴·哈格高塔拉里和RenéeJ？akel。

参考文献（References）

• Reza Abbasi-Asl, Yuansi Chen, Adam Bloniarz, Michael Oliver, Ben DB Willmore, Jack L Gallant, and Bin Yu. The deeptune framework for modeling and characterizing neurons in visual cortex area v4. bioRxiv, page 465534, 2018.
• Amina Adadi and Mohammed Berrada. Peeking Inside the Black-Box: A Survey on Explainable Artificial Intelligence (XAI). IEEE Access, 6:52138–52160, 2018. doi: 10.1109/ACCESS.2018.2870052.
• Claire Adam-Bourdarios, Glen Cowan, Cecile Germain, Isabelle Guyon, Balazs Kegl, and David Rousseau. Learning to discover: the higgs boson machine learning challenge. URL http://higgsml. lal. in2p3. fr/documentation, page 9, 2014.
• Abhijin Adiga, Chris J. Kuhlman, Madhav V. Marathe, Henning S. Mortveit, S. S. Ravi, and Anil Vullikanti. Graphical dynamical systems and their applications to bio-social systems. International Journal of Advances in Engineering Sciences and Applied Mathematics, Dec 2018. doi: 10.1007/s12572-018-0237-6.
• 等等