哈工大机器学习实验三--k-means聚类和混合高斯模型
一、实验目的
- 理解k-means聚类过程
- 理解混合高斯模型(GMM)用EM估计参数的实现过程
- 掌握k-means和混合高斯模型的联系
- 学会EM估计参数的方法和代码实现
- 学会用GMM解决实际问题
二、实验环境
- Win10,x86-64
- Pycharm 2019.1
- python 3.7.1
- 使用python库:numpy(计算),pandas (读写文件), sklearn(用于聚类验证), matplotlib.pyplot(用于可视化)
三、设计思想
3.1 算法原理
3.1.1 k-means聚类
k-means聚类就是根据某种度量方式(常用欧氏距离,如欧氏距离越小,相关性越大),将相关性较大的一些样本点聚集在一起,一共聚成k个堆,每一个堆我们称为一“类”。k-means的过程为:先在样本点中选取k个点作为暂时的聚类中心,然后依次计算每一个样本点与这k个点的距离,将每一个与距离这个点最近的中心点聚在一起,这样形成k个类“堆”,求每一个类的期望,将求得的期望作为这个类的新的中心点。一直不停地将所有样本点分为k类,直至中心点不再改变停止。
3.1.2 高斯混合模型
高斯混合模型是指具有如下形式的概率分布模型:
P ( y ∣ θ ) = ∑ k = 1 K α k φ ( y ∣ θ k ) P(y|\theta)=\sum_{k=1}^K \alpha_k \varphi(y|\theta_k) P(y∣θ)=k=1∑Kαkφ(y∣θk)
其中 α k \alpha_k αk是样本中类k中的数据所占的比率, ∑ k = 1 K α k = 1 \sum_{k = 1}^{K}\alpha_k = 1 ∑k=1Kαk=1, φ ( y ∣ θ k ) \varphi(y|\theta_k) φ(y∣θk)是第k类中的高斯分布的概率分布函数。
其中 φ ( y ∣ θ k ) \varphi(y|\theta_k) φ(y∣θk)具体为
φ ( y ∣ θ k ) = 1 2 π D 2 ∣ Σ k ∣ 1 2 e x p ( − ( y − μ k ) T Σ k − 1 ( y − μ k ) 2 ) \varphi(y|\theta_k)=\frac{1}{2\pi^{\frac{D}{2}}|\Sigma_k|^{\frac{1}{2}}}exp(-\frac{(y-\mu_k)^T\Sigma_k^{-1}(y-\mu_k)}{2}) φ(y∣θk)=2π2D∣Σk∣211exp(−2(y−μk)TΣk−1(y−μk))
其中D为样本数据的维数, Σ k \Sigma_k Σk为第k个高斯模型的协方差矩阵,如果数据为一维,则是方差; μ k \mu_k μk为第k个模型的均值。当样本为一维数据时
φ ( y ∣ θ k ) = 1 2 π σ k e x p ( − ( y − μ k ) 2 2 σ k 2 ) \varphi(y|\theta_k)=\frac{1}{\sqrt{2\pi}\sigma_k}exp(-\frac{(y-\mu_k)^2}{2\sigma_k^2}) φ(y∣θk)=2πσk1exp(−2σk2(y−μk)2)其中 σ k \sigma_k σk为第k类的标准差。
通常将 ( α , Σ , μ ) (\alpha ,\Sigma,\mu) (α,Σ,μ)记为 θ \theta θ,是高斯混合模型中的隐变量,由于隐变量的存在,高斯混合模型无法求出解析解,但是可以用EM算法迭代求解隐变量,并完成分类。
3.1.3 高斯混合模型参数估计的EM算法:
- 初始化响应度矩阵 γ \gamma γ, 协方差矩阵,均值和 α \alpha α
- E步:定义响应度矩阵 γ \gamma γ,其中 γ j k \gamma_{jk} γjk表示第j个样本属于第k类的概率,计算式如下
γ j k = α k φ ( y j ∣ θ k ) ∑ k = 1 K α k φ ( y j ∣ θ k ) , j = 1 , 2 , . . . , N ; k = 1 , 2 , . . . , K \gamma_{jk}=\frac{\alpha_k\varphi(y_j|\theta_k)}{\sum_{k=1}^{K}\alpha_k\varphi(y_j|\theta_k)},j=1,2,...,N;k=1,2,...,K γjk=∑k=1Kαkφ(yj∣θk)αkφ(yj∣θk),j=1,2,...,N;k=1,2,...,K - M步:将响应度矩阵视为定值,更新均值,协方差矩阵和 α \alpha α
μ k = ∑ k = 1 N γ j k y j ∑ j = 1 N γ j k , k = 1 , 2 , . . . , K \mu_k=\frac{\sum_{k=1}^{N}\gamma_{jk}y_j}{\sum_{j=1}{N}\gamma_{jk}} , k=1,2,...,K μk=∑j=1Nγjk∑k=1Nγjkyj,k=1,2,...,K
Σ k = ∑ j = 1 N γ j k ( y − μ k ) ( y − μ k ) T ∑ j = 1 N γ j k , k = 1 , 2 , . . , K \Sigma_k=\frac{\sum_{j=1}^N\gamma_{jk}(y-\mu_k)(y-\mu_k)^T}{\sum_{j=1}^{N}\gamma_{jk}},k=1,2,..,K Σk=∑j=1Nγjk∑j=1Nγjk(y−μk)(y−μk)T,k=1,2,..,K
p.s.注意,分子看似加和其实是对所有的样本求协方差矩阵,不能简单地求协方差矩阵后相加,必须同时乘以相应的权重,得到一个2xN的矩阵A,然后求得协方差矩阵 A A T AA^T AAT
4. 重复2.3.步,直到收敛。
3.2 算法的实现
3.2.0 参数介绍
self.data:保存样本点
self.K: 聚类的数目
self.dim:数据的维度
self.center : 存储中心点,使用np.array初始化数组时要注意:要定义为浮点数,否则会直接取整
self.n :样本数量
self.flags:记录k-means算法中每一个样本点属于哪一类
self.flags_em :记录GMM-EM算法中每一个样本点属于哪一类(由概率大小决策)
self.cov_all :保存k个高斯模型的协方差矩阵
self.u:保存k个高斯模型的均值
self.alpha :保存k个类的取值概率
self.r: 响应度矩阵
3.2.1 生成数据
使用numpy.random.multivariate_normal(mean,cov,data_num)生成4个高斯分布数据,其中协方差矩阵均为单位阵,并用f.write将数据写入’test.csv’文件中
mean1 = [1, 1]
mean2 = [1, 3]
mean3 = [3, 1]
mean4 = [3, 3]
cov1 = np.mat([[1, 0], [0, 1]])
data1 = np.random.multivariate_normal(mean1, cov1, 50)
data2 = np.random.multivariate_normal(mean2, cov1, 50)
data3 = np.random.multivariate_normal(mean3, cov1, 50)
data4 = np.random.multivariate_normal(mean4, cov1, 50)3.2.2 读取数据
使用pandas.read_csv从‘test.csv’中将数据读取出来,注意要在后面加上.values才能将DataFrame解析成ndArray(数组)
self.data = pd.read_csv("test.csv", header=None).values 3.2.3 k-means聚类
随机选取k个点作为中心点
利用random随机生成正整数,结合set()的互异性得到k个互不相等的正整数,将这k个样本点作为初始的k个类的中心
s = set()
# 生成K个随机正整数
while True:
if len(s) == self.K:
break
s.add(int(math.fabs(random.randint(0, self.n - 1))))
i = 0
for num in s:
self.center[i, 0] = self.data[num][0]
self.center[i, 1] = self.data[num][1]
i += 1计算所有样本点到中心的距离,并对样本点进行重新标记
for i in range(self.n):
flag = 0
min_length = MAX_INT
for j in range(self.K):
if min_length > self.cal_similarity(self.data[i, :], self.center[j, :]):
min_length = self.cal_similarity(self.data[i, :], self.center[j, :])
flag = j
self.flags[i] = flag
self.new_center()当两次标记的loss相差小于door的值时,算法结束。
3.2.4 GMM-EM算法
用k-means分类的结果初始化:沿用k-means得到的均值,计算k-means分类得到的各类的协方差矩阵作为各类初始的协方差矩阵
分别进行E步、M步的迭代steps次
while steps > 0:
steps -= 1
# E步求每个样本属于每个类的响应度
for j in range(self.n):
alpha_multi_fi = 0
for k in range(self.K):
# print(self.cal_probability(j, k))
alpha_multi_fi += self.alpha[k] * self.cal_probability(j, k)
for k in range(self.K):
fi = self.cal_probability(j, k)
self.r[j][k] = self.alpha[k] * fi / alpha_multi_fi
# M步更新参数
for k in range(self.K):
x1 = np.zeros((1, self.dim)) # 均值的分子
for j in range(self.n):
x1 += self.r[j][k] * self.data[j, :]
# 更新均值
x2 = self.data - np.tile(self.u[k], (self.n, 1)) # 数据与均值的差值,np.tile(复制矩阵)
x3 = np.eye(self.n) # 每个样本对于类别k的概率对角阵
for j in range(self.n):
x3[j][j] = self.r[j][k]
# 更新协方差矩阵
self.cov_all[k] = np.dot(np.dot(x2.T, x3), x2) / self.cal_echo(k)
# 更新alpha(每一类的概率)
self.alpha[k] = self.cal_echo(k) / self.n四、实验结果与分析
4.1 实验结果展示
生成的数据如下
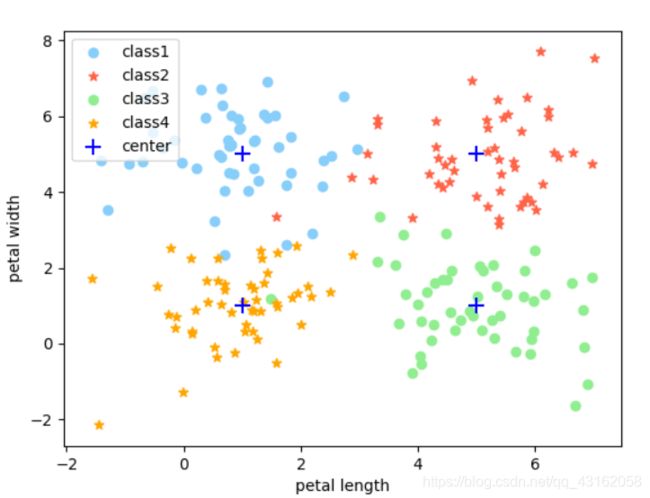
用k-means分类可得
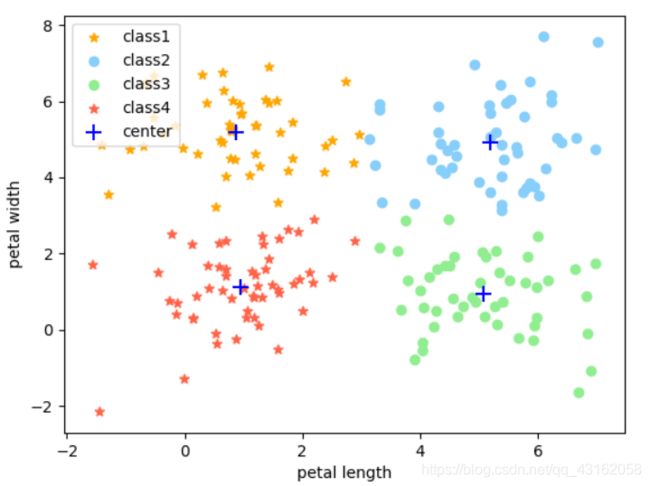
用GMM-EM分类可得
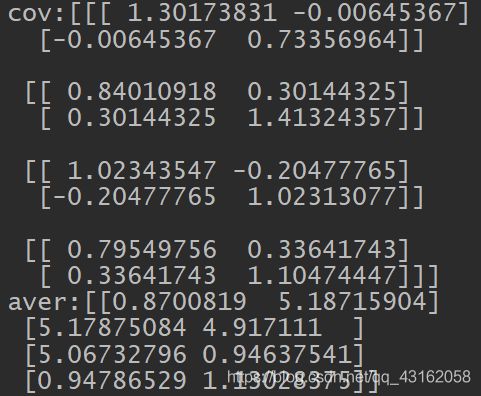
EM算法估计的参数结果如下
与sklearn的聚类结果比较
sklearn的参数, 均值几乎一模一样,但协方差有微小偏差
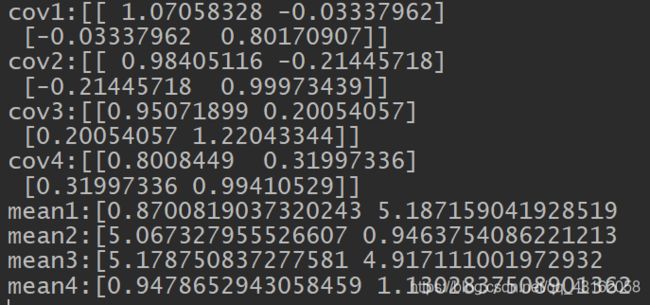
4.2 用真实数据集测试
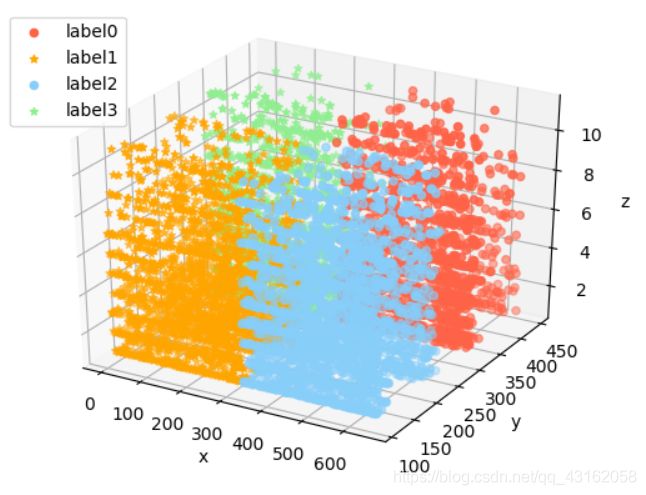
由于数据量较大,所以选取前8000个测试聚类效果
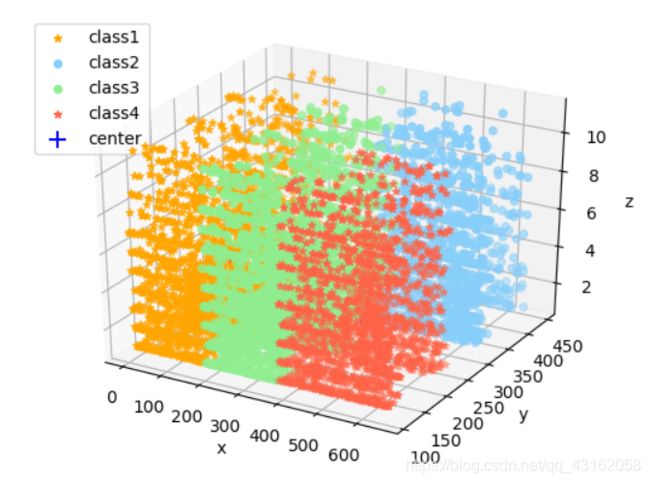
k-means的结果,聚类效果还挺好
GMM-EM以K-Means作为初值的结果
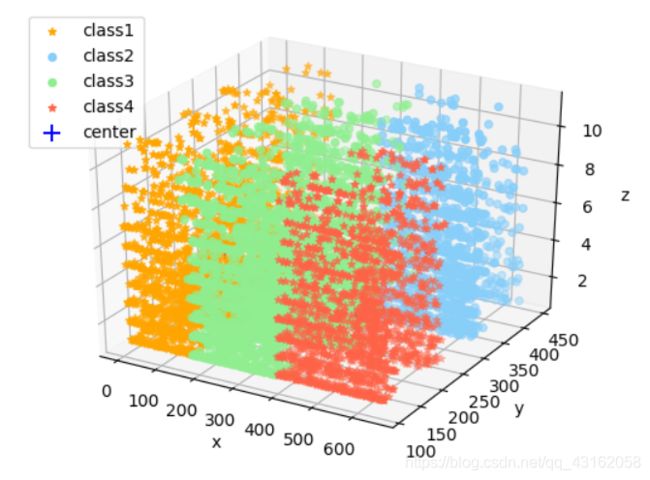
得协方差矩阵和均值
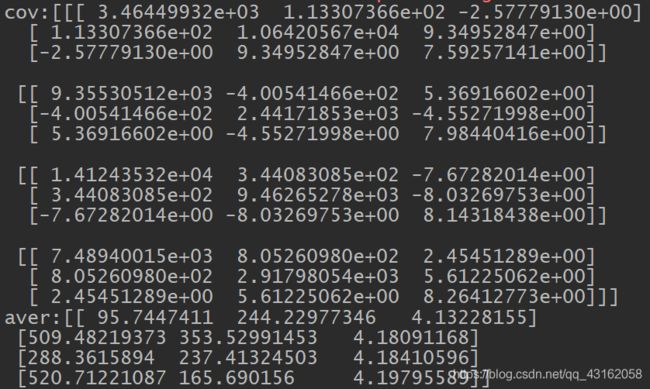
使用sklearn库分类可得
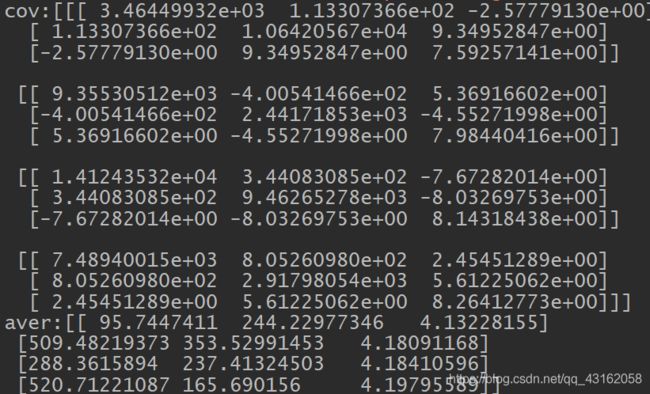
参数如下,和GMM-EM估计结果依然吻合,但是很奇怪的是,分类的图形并不完全一样
4.3 实验中遇到的问题及分析
4.3.1 关于协方差矩阵的迭代
之前一直以为是计算N个协方差矩阵,然后再将N个协方差矩阵的和作为第k类的新的协方差矩阵。我知道这样做肯定有问题,因为这样算得的协方差矩阵是非满秩的,也就意味着在下一轮迭代的时候协方差矩阵不可逆。以前一直没有理解这里的协方差矩阵的含义,其实这里的协方差矩阵相当于是关于类k对高斯混合模型中的每一个样本点求与中心点的偏差和,由于每个样本点属于类k的概率不同,因此还得乘以每个样本点属于类k的概率。
4.3.2 关于python的数据类型踩的坑
- numpy.matrix和numpy.array两者有区别,不能混用,numpy.matrix关于矩阵的运算更多,而numpy.array与c语言中的数组相似更多一些,但是两者也有一些共同点,比如都可以进行切片,可以计算矩阵的转置。
- numpy.array如果是自己定义,如果后面需要引入浮点数,一定要在初始定义的时候就加入浮点数,否则后面运算中出现的浮点数会被强制转化为整数,从而丢失精度。
4.3.3 涉及原理的一些坑
由于k-means选取的初始点是随机选取的,大多数情况下表现都还不错,但是有时候选择的点过于奇怪会导致k-means分类效果不太好 ,甚至出现和初始的分类完全不像的分类图。而且由于GMM-EM对初值敏感,导致GMM-EM参数估计的结果也会比较奇怪,但是这种概率很小。
比如下面这幅图就是初始值随机得不太正常的k-means分类结果
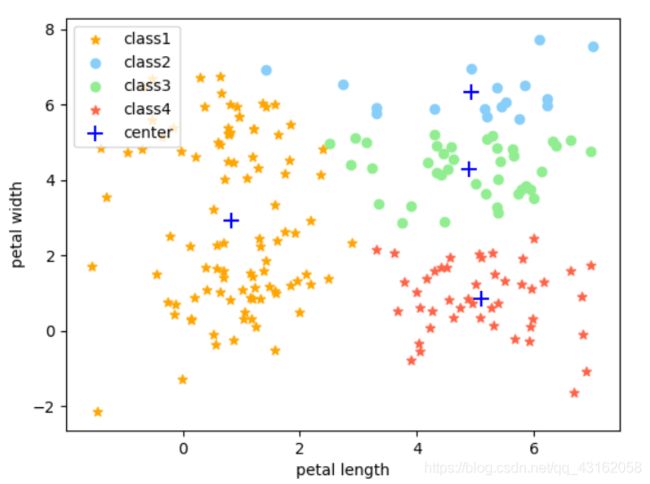
GMM-EM参数估计后分类结果如下,依然非常奇怪,而且增加迭代次数并不能改变这种情况
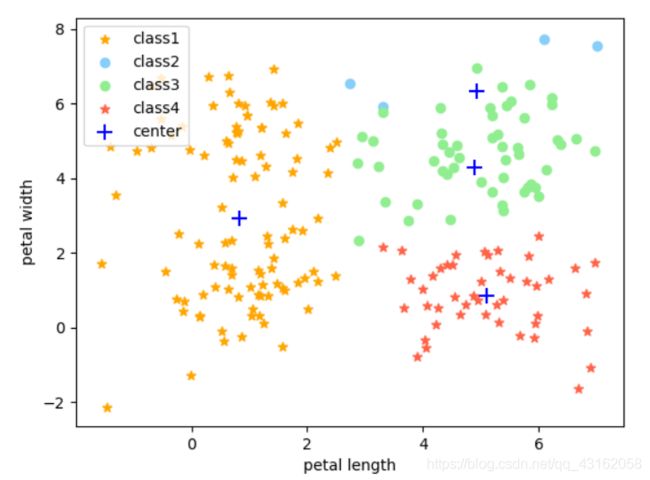
五、结论
- K-Means的分类结果受初始中心点的影响,我们可以通过一些求均值或者别的的方式寻找初始点来尽量减少这种影响;GMM-EM算法对初值的敏感程度更高,所以一般将K-Means得到的结果作为GMM-EM方法的初值。
- GMM-EM算法可以达到很高的准确度,计算结果可以和sklearn自带的聚类算法计算的结果几乎相同。
- K-Means和高斯混合模型比较:K-Means其实就是一种特殊的高斯混合模型,我们假设每种类在样本中出现的概率相等,都为 1 K \frac{1}{K} K1, 而且假设高斯模型中的每个变量之间是独立的,即变量间的协方差矩阵是对角阵,这样我们可以直接用欧氏距离作为K-Means的协方差去衡量相似性;K-Means对响应度也做了简化,每个样本只属于一个类,即每个样本属于某个类,则响应度为1,对于不属于的类,响应度直接设为0,算是对GMM的一种简化。而在高斯混合模型中,每个类的数据出现在样本中的概率为 α \alpha α, 用协方差矩阵替代K-Means中的欧式距离去度量点和点之间的相似度,响应度也由离散的0,1变成了需要通过全概率公式计算的值。但是由于GMM并未增加如K-Means那么多假设条件,分类最终效果比K-Means好,但是GMM-EM算法过于细化,容易被噪声影响,所以适合作为优化算法,即适合对K-Means的分类结果进行进一步优化。
六、参考文献
【统计学习方法】李航
附录:源代码
import pandas as pd
import numpy as np
import random
import matplotlib.pyplot as plt
import math
MAX_INT = 10000000 # 初始化为一个较大的值
DOOR = 1e-30 # k-means算法迭代结束的阈值
class GaussMix:
"""高斯混合模型"""
def __init__(self):
"""k-means的参数"""
self.data = pd.read_csv("test.csv", header=None).values # 读入多样本点
self.K = 4 # 聚几类
self.dim = len(self.data[0, :]) # 数据的维度
self.center = np.tile(np.array([[.0, .0]]), (self.K, 1)) # 存储中心点,使用np.array初始化数组时要注意:要定义为浮点数,否则会直接取整
self.n = len(self.data) # 样本数量
self.flags = list(range(self.n)) # 记录每一个样本点属于哪一族
self.flags_em = list(range(self.n))
"""高斯混合模型新增的参数"""
self.cov_all = [np.array([[2., 1.], [1., 2.]]), np.array([[3., 1.], [1., 4.]]), np.array([[2., 1.], [1., 2.]]),
np.array([[3., 1.], [1., 4.]])] # 保存协方差矩阵
self.u = np.array([[1., 2.], [6., 7.], [1., 2.], [1., 2.]]) # 均值
self.alpha = [0.25, 0.25, 0.25, 0.25] # 某一类的概率
self.r = np.zeros((self.n, self.K)) # 响应度矩阵
# 计算相似度(欧氏距离)
@staticmethod
def cal_similarity(lis1, lis2):
x = np.mat(lis1) - np.mat(lis2)
return np.dot(x, x.T)[0][0]
# 计算损失
def cal_loss(self):
ans = 0
for i in range(len(self.data)):
for j in range(len(self.center)):
# 每个点与每个中心计算欧式距离
ans += self.cal_similarity(self.data[i, :], self.center[j, :])
return ans
# 选择初始中心
def select_center(self):
s = set()
# 生成K个随机正整数
while True:
if len(s) == self.K:
break
s.add(int(math.fabs(random.randint(0, self.n - 1))))
i = 0
for num in s:
self.center[i, 0] = self.data[num][0]
self.center[i, 1] = self.data[num][1]
i += 1
# 更新各簇的中心点
def new_center(self):
for k in range(self.K):
cnt = 0 # 计数
a = np.zeros((1, self.dim)) # 统计和
for i in range(self.n):
if self.flags[i] == k:
cnt += 1
a += self.data[i, :]
a /= cnt # 均值
self.center[k] = a
# k-means算法
def k_means(self):
self.select_center()
loss1 = self.cal_loss()
while True:
loss0 = loss1
for i in range(self.n):
flag = 0
min_length = MAX_INT
for j in range(self.K):
if min_length > self.cal_similarity(self.data[i, :], self.center[j, :]):
min_length = self.cal_similarity(self.data[i, :], self.center[j, :])
flag = j # 寻找最近距离的类
self.flags[i] = flag # 重新标记
self.new_center() # 更新中心点
loss1 = self.cal_loss()
if np.fabs(loss1 - loss0) < DOOR:
break
# 可视化
def draw(self, sig):
x0 = []
y0 = []
x1 = []
y1 = []
x2 = []
y2 = []
x3 = []
y3 = []
for i in range(self.n):
x = self.flags[i]
if sig == 1:
x = self.flags_em[i]
if x == 0:
x0.append(self.data[i][0])
y0.append(self.data[i][1])
elif x == 1:
x1.append(self.data[i][0])
y1.append(self.data[i][1])
elif x == 2:
x2.append(self.data[i][0])
y2.append(self.data[i][1])
else:
x3.append(self.data[i][0])
y3.append(self.data[i][1])
plt.legend(loc=2)
plt.scatter(x0, y0, marker='*', c='orange', label='class1')
plt.scatter(x1, y1, marker='o', c='lightskyblue', label='class2')
plt.scatter(x2, y2, marker='o', c='lightgreen', label='class3')
plt.scatter(x3, y3, marker='*', c='tomato', label='class4')
plt.scatter(self.center[0, 0], self.center[0, 1], marker='+', color='blue', s=100, label='center')
for k in range(1, self.K):
plt.scatter(self.center[k, 0], self.center[k, 1], marker='+', color='blue', s=100)
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()
# 计算初值,根据训练得到的k-means模型计算均值和协方差矩阵
def cal_init(self):
# 初始均值
for i in range(self.K):
for j in range(self.dim):
self.u[i, j] = self.center[i, j]
# 初始协方差
cov = []
for i in range(self.K):
# 用每一类所有的样本计算每一类的协方差矩阵
array = []
for k in range(self.n):
if self.flags[k] == i:
array.append(self.data[k, :])
array = np.array(array)
aver = []
for k in range(len(array)):
aver.append(self.u[i, :])
aver = np.array(aver)
cov.append(np.dot((array - aver).T, array - aver))
self.cov_all = np.array(cov)
# 计算概率密度 第j个样本属于第k类的概率
def cal_probability(self, j, k):
# 分母
x1 = (2 * np.pi) ** (self.dim * 1.0 / 2) * np.linalg.det(self.cov_all[k]) ** 0.5
# 分子
x2 = np.exp(-0.5 * np.dot(np.dot((self.data[j, :] - self.u[k]), np.linalg.inv(self.cov_all[k])),
(self.data[j, :] - self.u[k]).T))
return x2 / x1
# EM估计高斯混合模型的参数
# 计算当为类k时,样本响应的概率和
def cal_echo(self, k):
ans = 0
for i in range(self.n):
ans += self.r[i][k]
return ans
def expectation_max(self, steps):
# print('init cov:' + str(self.cov_all))
# print('init aver:' + str(self.u))
while steps > 0:
steps -= 1
# E步求每个样本属于每个类的响应度
for j in range(self.n):
alpha_multi_fi = 0
for k in range(self.K):
# print(self.cal_probability(j, k))
alpha_multi_fi += self.alpha[k] * self.cal_probability(j, k)
for k in range(self.K):
fi = self.cal_probability(j, k)
self.r[j][k] = self.alpha[k] * fi / alpha_multi_fi
# M步更新参数
for k in range(self.K):
x1 = np.zeros((1, self.dim)) # 均值的分子
for j in range(self.n):
x1 += self.r[j][k] * self.data[j, :]
# 更新均值
x2 = self.data - np.tile(self.u[k], (self.n, 1)) # 数据与均值的差值,np.tile(复制矩阵)
x3 = np.eye(self.n) # 每个样本对于类别k的概率对角阵
for j in range(self.n):
x3[j][j] = self.r[j][k]
# 更新协方差矩阵
self.cov_all[k] = np.dot(np.dot(x2.T, x3), x2) / self.cal_echo(k)
# 更新alpha(每一类的概率)
self.alpha[k] = self.cal_echo(k) / self.n
print('cov:' + str(self.cov_all))
print('aver:' + str(self.u))
# 用最终得到的响应度进行分类
def div_em(self):
for j in range(self.n):
rec = 0
rate = 0
for k in range(self.K):
if self.r[j][k] > rate:
rec = k
rate = self.r[j][k]
self.flags_em[j] = rec
def main():
test = GaussMix()
test.k_means() # 先进行k-means训练
test.draw(0) # 画高斯分布得到的分类图
test.cal_init() # 用高斯分布得到的数据进行初始化
test.expectation_max(100) # EM算法进行参数估计
test.div_em() # 用高斯混合模型分类
test.draw(1) # 绘制分类图
main()