python计算机视觉——基础矩阵与对极几何

对极几何

多视图几何利用在不同视点拍摄的图像间关系研究相机或者特征之间的关系，而在多视图几何中最重要的基础就是双视图，如果已经有了一个场景的两个视图以及视图中的对应图像点，则依据相机位置关系，相机性质和三维场景点的位置可以得到图像点的几何关系约束，即对极几何。通过对极几何，我们可以在已知两幅图像中两点是对应关系的前提下，求解两个相机的相对位置和姿态。

如果仅看一个相机，我们并不能知道深度信息，可如果有两个相机的话（就像人有两只眼睛）我们就能得到深度的信息。

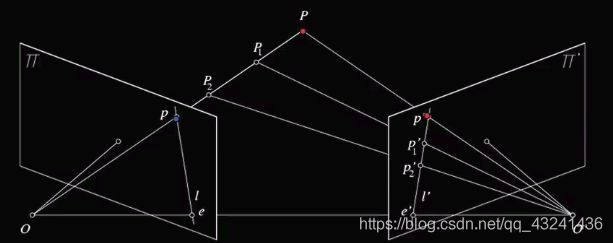
上图O和O’是两个相机中心，P点是物体所在，如果我们只看左边图像π上的点p，我们不能知道物体到底是在哪，点P1、P2或其他地方，可有了右边图像π’上的p’我们就能得到物体点P
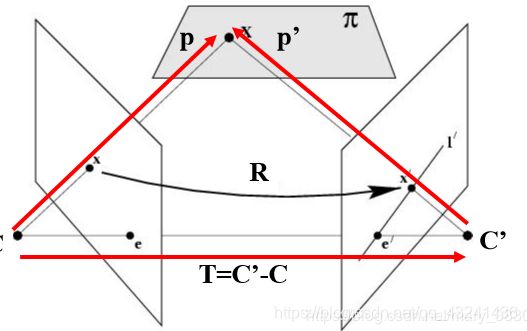
在上图，我们把两相机中心的连线OO’成为基线，把他们与观测物体的平面OO’P成为对极平面，对极平面与两相机图像的交线l和l’称为对极线，而OO’与两图像的交点e,e’就是对极点。
随着观测点P的上下移动，对极平面也会围绕基线旋转

我们可以看到在左图对极平面旋转时对极点是不变的，而在相机图像上所有对极线都会交于对极点，这个对极点就是另一个相机中心在其图像上的像，当然正如右图所示，对极点可以在图像外。

1. 本质矩阵与基础矩阵

本质矩阵（Essential matrix）
几何表示是便于理解的，可是计算机并不懂，我们要将其转为代数形式。
我们知道由相机1到相机2是刚体运动，那么观测点P在相机1坐标系的坐标就可以通过刚体转换变成相机2坐标系下，$$P^{\prime }=RP＋T$$

其中R和T分别表示旋转和平移，如果我们将其左叉乘一个T，即
$$T\times P^{\prime }=T\times RP＋T\times T=T\times RP$$

其中 表示对极平面的法线，若再左点乘一个P’得到
$$P^{\prime }（T\times P^{\prime }）=P^{\prime }(T\times RP)$$

由于P’与法线TxP’是垂直的，所以有
$$0=P^{\prime }(T\times RP)$$

我们知道两向量的叉乘可以转换为一向量的反对称矩阵与另一向量的点乘，于是
$$P^{\prime }（T\times RP）=P^{\prime }[T\times ]RP)=0$$
$[T\times ]$表示$T$的反对称矩阵，我们让$E=[T\times ]R$,那么
$P^{\prime T}\times EP=0$.
这个$E$就是本质矩阵.

本质矩阵采用的是相机的外部参数，也就是说采用相机坐标(The essential matrix uses CAMERA coordinates)，如果要分析数字图像，则要考虑坐标(u,v)，此时需要用到内部参数(To use image coordinates we must consider the INTRINSIC camera parameters)

基础矩阵
1）两幅图像之间的约束关系使用代数的方式表示出来即为基本矩阵。

2）基础矩阵F满足：$x^{T}F{x}^{\prime }=0$

3）基础矩阵可以用于简化匹配和去除错配特征。

原理：

设X在C,C′坐标系中的相对坐标分别为p,p′，则有 ： $$p=Rp\prime +Tp$$其中
$x=K^{\prime }p$
$x^{\prime }=K{p}^{\prime }$
$p=K^{-1}x$
$p^{\prime }=K^{\prime -1}{x}^{\prime }$

根据三线共面，有：$(p-T{)}^T(T\times p)=0转换为(R^T{p}^{\prime }{)}^T(T\times p)=0⇨T\times p=Sp$

还记得上文提到过的本质矩阵，本质矩阵描述的是：空间中的点在两个坐标系中的坐标对应关系。
根据前述，$K$和$K$’分别为两个相机的内参矩阵，有：

基础矩阵描述的是： 空间中的点在两个相平面中的坐标对应关系。

2. 估算基础矩阵F（8点法）

8点算法
8点法是通过对应点来计算基础矩阵的算法。
原理：
由于基础矩阵FFF定义为：$$x^{T}F{x}^{\prime }=0$$
任给两幅图像中的匹配点 x 与 x′ ，令 x=(u,v,1)T ，x’=(u’,v’,1)T，基础矩阵F是一个3×3的秩为2的矩阵，一般记基础矩阵F为：
$$F=\left[\begin{array}{ccc}{f}_{11}& f_{12}& f_{13}\\ f_{21}& f_{22}& f_{23}\\ f_{31}& f_{32}& f_{33}\end{array}\right]$$
有相应方程：$$u{u}^{\prime }11+u{v}^{\prime }f12+uf13+v{u}^{\prime }f21+v{v}^{\prime }f22+vf23+u^{\prime }f31+v\prime f32+f33=0$$
由矩阵乘法可知有：

在实际计算中，可以直接用$A^{T}A$的分解来求解参数。 也可以用非线性优化，通过搜索f使得$||Af||$最小化, 同时满足$||f||=1$的约束。上述求解后的F不一定能满足秩为2的约束，因此 还要在F基础上加以约束。通过SVD分解可以解决上述问题，令$F=U\Sigma V^T$
则 ：
$$\Sigma =\left[\begin{array}{ccc}{\sigma }_1& 0& 0\\ 0& {\sigma }_2& 0\\ 0& 0& {\sigma }_3\end{array}\right]$$
令
$${\Sigma }^{\prime }=\left[\begin{array}{ccc}{\sigma }_1& 0& 0\\ 0& {\sigma }_2& 0\\ 0& 0& {\sigma }_3\end{array}\right]$$
则最终解为：$F^{\prime }=U{\Sigma }^{\prime }{V}^T$

本矩阵有一个重要的特点就是奇异性，F矩阵的秩是2。如果基本矩阵是非奇异的，那么所计算的对极线将不重合。所以在上述算法解得基本矩阵后，会增加一个奇异性约束。 最简便的方法就是修正上述算法中求得的矩阵FFF。设最终的解为{F}′F′，令$detF\prime =0$下求得Frobenius范数（二范数）$\Vert F-F\prime \Vert$最小的F′。这种方法的实现还是使用了SVD分解，若$F=UD{V}^T$，此时的对角矩阵$D=diag(r,s,t)$，满足$r\ge s\ge t$，则$F^{\prime }=Udiag(r,s,0)V^T$最小化范数$\Vert F-F^{\prime }\Vert$，也就是最终的解。

基本步骤：
求线性解：由系数矩阵A最小奇异值对应的奇异矢量f求的F。
奇异性约束：是最小化Frobenius范数$\Vert F-F\prime \Vert$的F′代替F。

优点：
线性求解，容易实现，运行速度快 。
缺点：
对噪声敏感。

估算基础矩阵
步骤：

1. 导入两幅图像，并使用sift算法提取特征；
2. 使用函数match_twosided连接两幅图的特征；
3. RANSAC去除错误点匹配；
4. 归一化8点算法估计基础矩阵。这是通过对应点来计算基础矩阵的算法。

# -*- coding: utf-8 -*-
from PIL import Image
from numpy import *
from pylab import *
import numpy as np
from PCV.geometry import camera
from PCV.geometry import homography
from PCV.geometry import sfm
from PCV.localdescriptors import sift
# -*- coding: utf-8 -*-

im1 = array(Image.open('picture/home/1.jpg'))
im2 = array(Image.open('picture/home/2.jpg'))

sift.process_image('picture/home/1.jpg', 'im1.sift')
l1, d1 =sift.read_features_from_file('im0.sift')

sift.process_image('picture/home/2.jpg', 'im2.sift')
l2, d2 =sift.read_features_from_file('im1.sift')

matches = sift.match_twosided(d1, d2)
ndx = matches.nonzero()[0]
x1 = homography.make_homog(l1[ndx, :2].T)
ndx2 = [int(matches[i]) for i in ndx]
x2 = homography.make_homog(l2[ndx2, :2].T)

d1n = d1[ndx]
d2n = d2[ndx2]
x1n = x1.copy()
x2n = x2.copy()

figure(figsize=(16,16))
sift.plot_matches(im1, im2, l1, l2, matches, True)
show()

def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
    """ Robust estimation of a fundamental matrix F from point
    correspondences using RANSAC (ransac.py from
    http://www.scipy.org/Cookbook/RANSAC).

    input: x1, x2 (3*n arrays) points in hom. coordinates. """

    from PCV.tools import ransac
    data = np.vstack((x1, x2))
    d = 10 # 20 is the original
    # compute F and return with inlier index
    F, ransac_data = ransac.ransac(data.T, model,
                                   8, maxiter, match_threshold, d, return_all=True)
    return F, ransac_data['inliers']

# find E through RANSAC
model = sfm.RansacModel()
F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-4)

print(len(x1n[0]))
print(len(inliers))

# 计算照相机矩阵（P2 是 4 个解的列表）
P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2 = sfm.compute_P_from_fundamental(F)

# triangulate inliers and remove points not in front of both cameras
X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2)

# plot the projection of X
cam1 = camera.Camera(P1)
cam2 = camera.Camera(P2)
x1p = cam1.project(X)
x2p = cam2.project(X)

figure()
imshow(im1)
gray()
plot(x1p[0], x1p[1], 'o')
#plot(x1[0], x1[1], 'r.')
axis('off')

figure()
imshow(im2)
gray()
plot(x2p[0], x2p[1], 'o')
#plot(x2[0], x2[1], 'r.')
axis('off')
show()

figure(figsize=(16, 16))
im3 = sift.appendimages(im1, im2)
im3 = vstack((im3, im3))
imshow(im3)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1p[0])):
    if (0<= x1p[0][i]0: #plot([locs1[i][0],locs2[m][0]+cols1],[locs1[i][1],locs2[m][1]],'c')
        x1=int(l1[i][0])
        y1=int(l1[i][1])
        x2=int(l2[int(m)][0])
        y2=int(l2[int(m)][1])
        # p1 = array([l1[i][0], l1[i][1], 1])
        # p2 = array([l2[m][0], l2[m][1], 1])
        p1 = array([x1, y1, 1])
        p2 = array([x2, y2, 1])
        # Use Sampson distance as error
        Fx1 = dot(F, p1)
        Fx2 = dot(F, p2)
        denom = Fx1[0]**2 + Fx1[1]**2 + Fx2[0]**2 + Fx2[1]**2
        e = (dot(p1.T, dot(F, p2)))**2 / denom
        x1e.append([p1[0], p1[1]])
        x2e.append([p2[0], p2[1]])
        ers.append(e)
x1e = array(x1e)
x2e = array(x2e)
ers = array(ers)

indices = np.argsort(ers)
x1s = x1e[indices]
x2s = x2e[indices]
ers = ers[indices]
x1s = x1s[:20]
x2s = x2s[:20]

figure(figsize=(16, 16))
im3 = sift.appendimages(im1, im2)
im3 = vstack((im3, im3))
imshow(im3)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1s)):
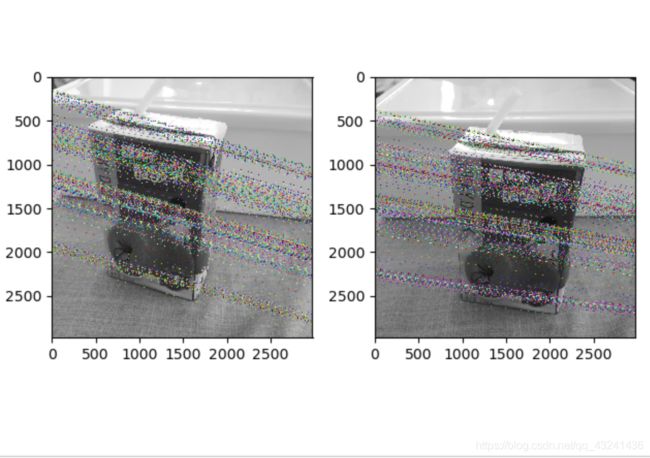
    if (0<= x1s[i][0]

SIFT对两个图像进行特征提取以及匹配，然后使用归一化8点算法进行基本矩阵的求解，并且把两个视图的对极线都画出。

运行结果：
sift匹配：

RANSAC去除错误点匹配：

八点算法结果：

基本矩阵为：

可以看到，八点算法得到的特征匹配连线最为准确和干净。

3. 外极点和外极线

首先我们需要在两个图像之间找到尽可能多的匹配项，以找到基本矩阵。为此，我们将SIFT描述符与基于FLANN的匹配器和比率测试结合使用。

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
img1 = cv.imread('myleft.jpg',0)  #索引图像 # left image
img2 = cv.imread('myright.jpg',0) #训练图像 # right image
sift = cv.SIFT()
# 使用SIFT查找关键点和描述符
kp1, des1 = sift.detectAndCompute(img1,None)
kp2, des2 = sift.detectAndCompute(img2,None)
# FLANN 参数
FLANN_INDEX_KDTREE = 1
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
search_params = dict(checks=50)
flann = cv.FlannBasedMatcher(index_params,search_params)
matches = flann.knnMatch(des1,des2,k=2)
good = []
pts1 = []
pts2 = []
# 根据Lowe的论文进行比率测试
for i,(m,n) in enumerate(matches):
    if m.distance < 0.8*n.distance:
        good.append(m)
        pts2.append(kp2[m.trainIdx].pt)
        pts1.append(kp1[m.queryIdx].pt)

现在，我们获得了两张图片的最佳匹配列表。 让我们找到基本面矩阵。

pts1 = np.int32(pts1)
pts2 = np.int32(pts2)
F, mask = cv.findFundamentalMat(pts1,pts2,cv.FM_LMEDS)
# 我们只选择内点
pts1 = pts1[mask.ravel()==1]
pts2 = pts2[mask.ravel()==1]

接下来，我们找到Epilines。在第二张图像上绘制与第一张图像中的点相对应的Epilines。因此，在这里提到正确的图像很重要。我们得到了一行线。因此，我们定义了一个新功能来在图像上绘制这些线条。

def drawlines(img1,img2,lines,pts1,pts2):
    ''' img1 - 我们在img2相应位置绘制极点生成的图像
        lines - 对应的极点 '''
    r,c = img1.shape
    img1 = cv.cvtColor(img1,cv.COLOR_GRAY2BGR)
    img2 = cv.cvtColor(img2,cv.COLOR_GRAY2BGR)
    for r,pt1,pt2 in zip(lines,pts1,pts2):
        color = tuple(np.random.randint(0,255,3).tolist())
        x0,y0 = map(int, [0, -r[2]/r[1] ])
        x1,y1 = map(int, [c, -(r[2]+r[0]*c)/r[1] ])
        img1 = cv.line(img1, (x0,y0), (x1,y1), color,1)
        img1 = cv.circle(img1,tuple(pt1),5,color,-1)
        img2 = cv.circle(img2,tuple(pt2),5,color,-1)
    return img1,img2

现在，我们在两个图像中都找到了Epiline并将其绘制。

# 在右图（第二张图）中找到与点相对应的极点，然后在左图绘制极线
lines1 = cv.computeCorrespondEpilines(pts2.reshape(-1,1,2), 2,F)
lines1 = lines1.reshape(-1,3)
img5,img6 = drawlines(img1,img2,lines1,pts1,pts2)
# 在左图（第一张图）中找到与点相对应的Epilines，然后在正确的图像上绘制极线
lines2 = cv.computeCorrespondEpilines(pts1.reshape(-1,1,2), 1,F)
lines2 = lines2.reshape(-1,3)
img3,img4 = drawlines(img2,img1,lines2,pts2,pts1)
plt.subplot(121),plt.imshow(img5)
plt.subplot(122),plt.imshow(img3)
plt.show()

以下是不同情境下运行的结果

1）左右拍摄，极点位于图像平面上

2）像平面接近平行，极点位于无穷远

3）图像拍摄位置位于前后

4. 总结与结论

• 实验遇到的困难及解决办法：
  1.python3安装opencv
  安装指南：在Windows中安装OpenCV-Python/
  还可以通过cmd——>pip install python-opencv安装
  2.极线的运行中会报错：AttributeError: module ‘cv2.cv2’ has no attribute ‘SIFT’
  解决：将sift = cv2.SIFT()替换为：sift = cv2.xfeatures2d.SIFT_create()
  分析：opencv将SIFT等算法整合到xfeatures2d集合里面了。写法：sift = cv2.xfeatures2d.SIFT_create()
  说明：问题产生的环境
  Python版本：3.7.2
  OpenCV版本：3.4.2
  原博解决

• 基本矩阵的特性

  1. rank (F) = 2 (基本矩阵的秩为2，非常重要)

  2. 基本矩阵依赖内部和外部参数（Intrinsic and Extrinsic Parameters) （f, R & T）决定。

  3. 使用像素坐标系

  4. F就是左边图像到右边图像的基本矩阵，从公式上可以看出基本矩阵是有方向的，右图到左图的基本矩阵就是F的转置

  5. F矩阵是一个7个自由度的33矩阵(33矩阵本身9个自由度，因为相差一个常数因子和行列式值为0两个条件，减掉2个自由度)，相差一个常数因子的意思是：kF(k!=0)也是基本矩阵，也就是说如果F是基本矩阵，那么kF也是基本矩阵，所以基本矩阵不唯一，在相差一个倍数的前提下是唯一的，也就是我们可以固定矩阵中某一个非零元素的值，这样自然少一个自由度。

  6. 属性表
     

• 基本矩阵的作用

  1. 与本质矩阵类似，基本矩阵也告诉我们一个图像中的像素如何与另一个图像的极线相关联。
     (像素坐标系：像素–>极线)
  2. 三维重建和特征匹配上
  3. 基本矩阵独立于场景结构
  4. 它可由场景点在图像中的对应关系进行计算，而不需要摄像机的内参和外参来进行计算。
  5. 相反，可以先求出F，然后根据F求出摄像机的外参(R, T)

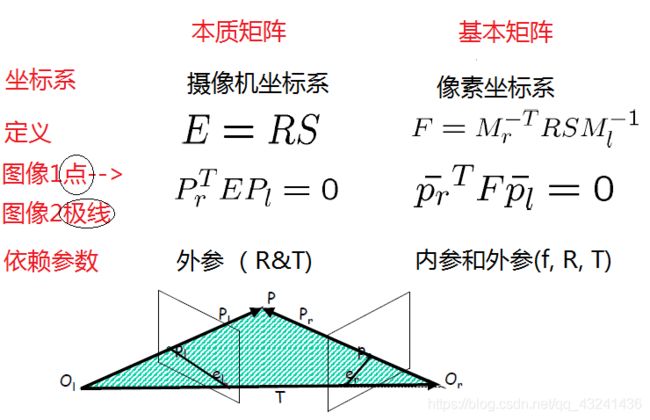
• 本质矩阵与基本矩阵的比较

参考博客
参考博客
参考博客
参考博客https://panchuang.net/2020/03/31/opencv-python-系列-五十-对极几何/