2021-05-12翻译

MP-SPDZ: A Versatile Framework for Multi-Party Computation 2020

Marcel Keller
CSIRO’s Data61
Australia
[email protected]
[email protected]

摘要：多协议SPDZ (MP-SPDZ)是SPDZ-2 (Keller等人，CCS 13)的一个分支，SPDZ是被称为SPDZ (Damgård等人，Crypto 12)的多方计算(MPC)协议的实现。MP-SPDZ将SPDZ-2扩展为30个MPC协议变体，所有这些变体都可以与基于Python的相同高级编程接口一起使用。这大大简化了比较不同协议和安全模型的成本。

实现的协议的广度加上一个可访问的高级接口，使它适合于在各种安全模型中计算成本的基准，无论是有或没有安全计算背景的研究人员

本文概述了MP-SPDZ开发过程中实现的各种协议和设计选择，以及编程接口的功能。

1.引言

多方计算允许一组各方对他们的私有输入进行协作计算，而除了结果之外不显示任何其他内容。
已经提出了一系列的应用，如真实拍卖[BDJ+06]，避免卫星碰撞[HLOI16]，计算性别薪酬差距[LVB+16]，或隐私保护机器学习[MZ17]。在20世纪80年代基础理论发展之后[CCD88, BGW88]， 2009年Pinkas等人[PSSW09]在软件中首次实现。从那时起，已经为一系列安全模型和计算领域创建了许多框架。我们所说的安全模型是指对各方行为的假设，特别是假设有多少人的行为是诚实的，以及不诚实的各方是否遵循协议或试图获取信息或通过偏离而损害结果。另一方面，计算域表示一种数学结构，该结构用于表示底层方案所要求的计算中的秘密信息。在应用中，定义域通常采用一个环的形式，即具有两个类似加法和乘法运算的集合。通常说的环是简单地由带模的整数运算定义的，但也有其他的例子，如特征二的伽罗瓦域(例如，它定义了AES的算术结构)。

几乎所有开放的用于多方计算的框架都局限于特定的安全模型和计算领域，这使得很难评估一个安全模型与另一个安全模型的成本，因为必须多次实现相同的计算。同样，很难比较同一安全模型中的协议。MP-SPDZ（https://github.com/data61/mp-spdz）的目标是改变这一点，它提供了一个使用相同虚拟机的30种协议变体的实现，以及一个编译器，该编译器将高级代码编译为字节码，以便由该虚拟机执行。这允许在各种设置中对计算进行基准测试之前，只实现一次计算。

在一个框架中结合许多协议的方法的核心是这样一种直觉:虽然存在差异,但所有用于安全计算的常用协议在很大程度上可以简化为几个相似的操作，这些都是输入、输出、局部可计算的线性操作，一个更复杂的操作，如与或乘法，并生成相关的随机性，如随机位。因此，为了尽可能多地重用组件和优化，构建一个通用框架来促进此蓝图似乎很自然。MP-SPDZ这样做的同时，仍然允许在必要时增加特定的协议。

MP-SPDZ基于SPDZ-2 [KRSS18, KSS13]，实现了SPDZ协议[DPSZ12, DKL+13]。SPDZ-2的基础设施已在一系列工作中使用和扩展[KS14, KOS15, KOS16, Kel17, KY18, KPR18, DEF+19]。Araki等人[ABF+18]已采取步骤，在SPDZ-2中整合除SPDZ以外的其他协议。然而，他们的方法由于过度依赖库调用来实现共享添加等基本操作而受到损害，因此效率相对较低。这可以从SPDZ与更简单的诚实多数协议的比较中看出(Araki等人的图6-8)，因为前者是在SPDZ-2中原生实现的。MP-SPDZ不是基于Araki等人的工作，而是直接从SPDZ-2分叉。

2018年上半年可用的运输框架。他们估计，在所有框架中创建和运行三个简单的示例程序总共需要750人小时。MP-SPDZ的目标是通过为每个发行版提供独立的Linux二进制文件和为高级语言提供大量文档来降低安全计算的门槛（https://mp-spdz.readthedocs.org）。此外，它使用了一个持续集成工具，在GitHub上提交的问题通常在几天内就会得到解决。

Paper organization. 

在介绍了类似的框架(使用比较基准)和基本概念之后，我们将一层一层地进行，从底层协议到高级库。

作为贯穿整个论文的一个锚点，我们将使用计算由两个不同方提供的两个向量的内积的例子。Hastings等人将此作为他们的例子之一。MP-SPDZ的代码如图1所示。

1.1 Comparison to Other Frameworks

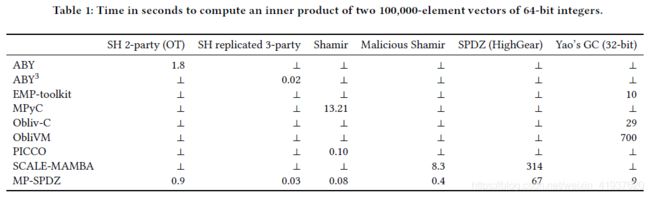
下面我们将考虑Hastings等人描述的所有框架，以及在撰写本文时添加到其存储库中包含示例程序和构建环境的框架[HHNZ20]。如果可用，我们也指出内积例子的近似大小。表1突出了MP-SPDZ与其他框架的比较。SH代表半诚实的安全。详见1.2节。

ABY. 该框架仅实现了具有半诚实安全性的两方计算[DSZ15]。然而，与MP-SPDZ不同的是，它提供了秘密共享计算和乱码电路之间的转换。内积的例子使用了大约60行代码，没有注释或空行。

ABY3.  该框架仅实现了具有诚实多数和半诚实安全的三方计算[MR18]。内积的例子使用了大约40行代码，没有注释或空行。

CBMC-GC. 这是一个编译器，将C代码编译成二进制电路描述[BHWK16]，由ABY执行。Hastings等人无法通过他们的例子使其工作。

EMP-toolkit. 该框架仅实现各种安全模型中的混淆电路[WMK16]。如果没有使用姚的半诚实安全的乱码电路，循环将在编译时展开。内积示例使用了大约60行代码，没有注释或空行。

FRESCO. 该框架[Ale20]只实现不诚实的多数计算，对算术电路(SPDZ和)具有恶意安全，对二进制电路具有半诚实安全[DNNR17]。内积示例使用了大约30行代码，没有注释或空行。

Frigate. 这是一个编译器，将类似c的代码编译为二进制电路描述[MGC+16]。与MP-SPDZ不同，循环总是在编译时展开。内积示例使用了大约20行代码，没有注释或空行。

JIFF. 这个JavaScript库只实现了诚实-多数计算和半诚实安全作为一个整体[Tea20]。与MP-SPDZ不同，它允许在脱机和在线阶段之间更改安全模型。内积示例使用了大约50行代码，没有注释或空行。

MPyC. 这个Python框架[Sch20]只实现了基于Shamir的秘密共享[Sha79]的半诚实安全计算。内积示例使用了大约20行代码，没有注释或空行。

Obliv-C. 该框架通过标准C [ZE15]编译C语言到机器码的扩展。它只以半诚实的安全性支持姚的乱码电路。内积示例使用了大约20行代码，没有注释或空行。

OblivVM. 这个框架编译Java到Java字节码的扩展[LWN+15]。它只是用半诚实的安全措施来支持姚混乱的线路。内积示例使用了大约20行代码，没有注释或空行。

PICCO. 这个框架通过标准C [ZSB13]将C语言的扩展编译为本机二进制文件。它仅实现了基于Shamir秘密共享的诚实多数的半诚实计算。内积示例使用大约10行代码，没有注释或空行。

SCALE-MAMBA. 这个框架[COS19]是SPDZ-2 [KSS13, KRSS18]的另一个分支。尽管有共同的根源，但自2018年以来，这两个分支已经出现了相当大的分化。SCALE-MAMBA只实现对质数取模(而不是对2的幂取模)的算术计算，Hazay等人[HSS17]提出的乱码电路，以及基于秘密共享的二进制计算[FKOS15, WRK17]。所有的计算仅用恶意安全实现，对素数取模的不诚实多数计算仅用同态加密实现。另一方面，SCALE-MAMBA在理论上为任何可能的访问结构实现诚实多数计算。

前端类似于MP-SPDZ，但没有后来添加的动态循环优化(第6.3节)、重复代码优化(第6.4节)和机器学习功能(第7.3节)。此外，作者已经开始从Python编译器转向基于Rust的新编译器。内积示例使用不到10行代码，没有注释或空行。

Sharemind MPC. 这个框架为各种后端实现了一个前端，但它自己的后端只使用了具有诚实多数的三方半诚实计算[BLW08]。它还允许使用ABY和FRESCO作为后端，而专有后端不是免费的。内积示例使用不到10行代码，没有注释或空行。

TinyGarble. 这个框架只实现姚的半诚实安全的乱码电路[SHS+15]。Hastings et al.无法使其工作与他们的例子。

Wysteria. 该框架实现了一种特定于领域的语言，仅在不诚实多数的半诚实设置下进行二进制计算[RHH14]。Hastings等人无法在这个框架中运行他们的所有示例。

1.2 Benchmarks

我们已经对MP-SPDZ与前一节中列出的其他框架进行了基准测试（The code can be found at https://github.com/mkskeller/mpc-benchmarks）。表1显示了在一台使用第7代i7处理器(基线频率为2.8 GHz)的机器上计算长度100,000的内积需要多少秒。我们选择了本地计算，因为并不是所有的框架都支持在不同的主机上执行。

为了进行基准测试，我们在MP-SPDZ代码中用get_raw_input_from()替换了get_input_from()。这是因为前者导致使用c++标准库的istream功能读取输入，这大大增加了一些基准测试的时间。其他框架中的示例要么使用像atoi()这样更快的函数，要么使用硬编码的输入。

此外,素数(Shamir和SPDZ)的计算模的计时已经使用了128位的素数，因为这是一个常见的选择，因为许多算法需要(k + s)位的素数来进行k位计算和安全参数s。为了更公平的比较，我们已经将SCALE-MAMBA中的所有统计安全参数减少到40。类似地，HighGear图排除了密钥生成，因为这两个框架处理这个问题的方式不同。

从表中可以看出，使用虚拟机的更复杂的方法不会显著降低算术计算的性能。

此外，我们使用Yao的乱码电路进行了基准测试，但使用的是32位整数而不是64位整数，因为有些例子只支持前者。

请注意，⊥意味着特定的框架不实现特定的协议，除了ABY和Yao的情况，其中没有可用的示例代码。

我们已经确定了导致框架性能显著下降的许多原因。MPyC和obilvm不是用C/ c++实现的。对于SCALE-MAMBA，我们发现由于经常使用变长整数，它利用了频繁的分配/空闲调用，并且它使用大量相对昂贵的函数调用MPIR来进行固定长度的算术。此外，它还生成了比所需更多的预处理数据。

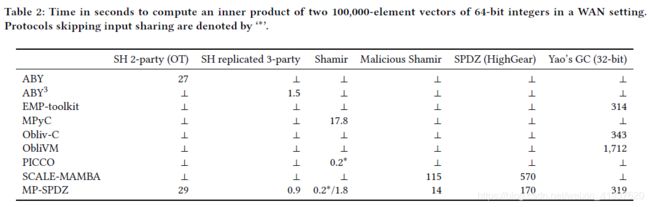
最后，表2和表3显示了我们在模拟WAN设置(100mbit /s和100ms RTT)以及总通信中的框架图。
后者是在所有其他框架的Docker中使用ip -s link lo获得的。

Missing frameworks. 我们没有为1.1节中提到的各种框架提供基准测试，原因如下:

• 没有有效的内积例子:CBMC-GC, TinyGarble，Wysteria
• 没有后端执行实际计算:Frigate
• 内积示例不完整(没有预处理):FRESCO
• 使用JavaScript: JIFF
• 软件不可用:Sharemind MPC

2 PRELIMINARIES

在本节中，我们将解释安全多方计算中的各种基本概念。

Security models. 多方计算协议的一个核心属性是对各方的假设，这些假设发生在两个轴上。第一个问题是，有多少人的行为被认为是诚实的，有多少人被认为在某种程度上是腐败的。MP-SPDZ中的协议都假设了阈值损坏，即有一定数量的当事人被认为是腐败的。诚实的多数和不诚实的多数之间有很大的区别，也就是说，这个门槛是否严格低于参与人人数的一半。对于不诚实的大多数人来说，协议通常更复杂、更昂贵。

第二个问题是腐败参与人的行为。这里的两个主要类别是，它们是否仍然遵循协议，但在提取信息时串谋(称为半诚实或被动破坏)，或者它们是否为了获取信息或扭曲计算结果而偏离协议(称为恶意或主动破坏)。后一种设置提出了进一步的问题，即如果出现偏差(保证输出)，计算是否还能继续进行，以及在诚实方不这样做(公平性)的情况下，被损坏的一方是否能学习到结果。MP-SPDZ中所有带有恶意安全的协议都在“带有中止的恶意”模型中工作，这意味着检测到偏差，但之后协议无法恢复。原因在于，公平相对昂贵，而对于不诚实的大多数人来说，保证产出是完全不可能的。考虑两方协议的情况:当另一方停止通信时，一方不能继续。

Computation domains. 在多方计算中，有各种各样的数学结构。这通常采用整数对某个数m取模的形式。如果m = 2，计算就变成了二进制电路，因为加法对应XOR，乘法对应AND。对于更大的M，文献建立了算术电路这个术语，因为提供的基本运算仍然是加法和乘法。如果M是一个素数，定义域满足一个域的定义，即除0外的所有数都有一个乘法逆。这对于包括Shamir的秘密共享[Sha79]和SPDZ [DPSZ12]在内的许多方案都是必需的。对于后者，这些要求后来被调整为计算一个模幂，从而产生了协议。然而，用素数取模的整数计算并不是有限域的唯一例子。MP-SPDZ也在中实现计算。后者尤其适用于对称密码系统，如基于算法的AES。

Secret sharing. 这种信息分布的概念是许多多方计算协议的核心。信息的分发方式允许一些集合(called qualified称为限定的)对其进行重构，而一些较小的集合(called unqualified称为非限定的)不能从给定的共享中推断出任何东西。哪些子集可以恢复、哪些不能恢复的确切定义称为访问结构。显然，限定集的超集也必须是限定的，非限定集合的子集必须是非限定的，这样访问结构才有意义。此外，秘密共享的共同定义要求各方的所有子集要么是限定的，要么是非限定的。

在范围内的数字x被各方P1, . . . , Pn通过发送随机数到Pi，使。可以很容易地看出，所有各方一起可以重构x，而任意严格子集的视图无法被一组随机数所区分。除基于乱码的协议外，该秘密共享方案适用于所有具有不诚实多数的协议。

其他秘密共享方案中使用MP-SPDZ包括replicated  secret sharing(BL90)始于additive secret sharing，但发送多个共享给每个方和Shamir的秘密共享[Sha79]，其中，份额是用固定次数的随机多项式来确定的，它等于被破坏的参与方的最大数目。

所有这些秘密共享方案都是线性的，也就是说，由于重构也是线性的，所以秘密共享值的任何(仿射)线性组合都可以局部计算。

Beaver’s multiplication. 该技术[Bea92]将秘密数的乘法简化为秘密随机数的乘法，在安全性和实用性方面都很有用。首先，它允许在检查双方是否遵守协议之前乐观地执行秘密随机数的乘法。如果检查失败，协议可以中止而不产生任何后果，因为秘密随机性独立于实际的秘密数据。其次，即使实际的计算是顺序的，Beaver的乘法也可以进行批处理预处理，这在使用(仅)允许一次有效地加密多个值的基于格的密码系统时是一个特别的优势。假设[x]表示x的秘密共享，并假设独立的随机a和b有一个三重([a]， [b]， [ab])。揭示x + a和y + b后，就可以计算出[x]和[y]的乘法。揭示这些并不能揭示x或y，因为a和b是秘密的，是随机选择的。在揭示了总数之后，各方开始计算

[xy] = [(x + a − a) · (y + b − b)]
= (x + a) · (y + b) − (x + a) · [b] − (y + b) · [a] + [ab].

注意，这个计算对于秘密值是仿射线性的，因此可以用任何线性秘密共享方案来计算它。

Oblivious transfer.  这是一个基本的两方加密协议，它是第一个被用于不诚实多数计算的协议。本质上，一方(称为发送方)输入两个字符串s_0、s_1，另一方(称为接收方)输入位b并学习s_b。关键是，发送方没有学习b，接收方也没有学习s_(1−b)。相对来说，从遗忘传输构造一个协议是很简单的，它允许双方在不透露输入的情况下计算各自已知的私有号码的乘积的秘密共享。该构造由MASCOT[KOS16]等协议来利用。我们只知道遗忘传输是由公开密钥密码学构造的。然而，OT扩展[ikp03]可以用来保持使用这种更昂贵的方案在一个较低的常数，同时使用更对称的加密代替。

Homomorphic encryption. 这指的是一种加密方案，能够在不显示明文的情况下有效地对密文进行操作。虽然有限同态的加密方案已经被知道有一段时间了(教科书RSA在某种意义上是同态的)，但只有基于格的密码学的出现才导致方案在两个操作上是同态的。MP-SPDZ采用了Brakerski等人[BGV12]提出的分层加密方案，该方案要求对一个数字向量进行一次加密。最小长度取决于明文模数，但通常范围从几千到几万。具体实现基于Gentry等[GHS12]的方法，该方法采用Montgomery表示[Mon85]和快速傅里叶变换来定义。第一种方法便于对素数求模而不需要昂贵的模约简，第二种方法是将一组数转换为明文空间中的一个多项式的有效方法，使两个这样的多项式的乘法对应于这些数的元素级乘积。这种方法限制了可以使用的素数模，但许多应用只需要一般的类整数计算，与实际的素数无关。

3 THE PROTOCOLS

表4显示了在MPSPDZ中实现的每个安全模型和计算域组合中的协议变体。在下面的部分中，我们将简要描述它们。

3.1 Dishonest Majority

所有协议的不诚实多数使用的技术有关的公开密钥密码学，或不经意传输同态加密。Nielsen等人[NNOB12]和Damgård等人[DPSZ12]开始了这方面的实际协议研究。前者提出了一种基于不经意传输的两方协议(后来被称为TinyOT)计算二进制电路，后者提出了一种利用同态加密(以作者的名字命名为SPDZ)进行领域计算的多方协议(以素数模或模计算)。两者都使用Beaver技术将计算划分为数据独立阶段和数据依赖阶段[Bea92]。前者(有时称为脱机)输出后者使用的相关信息以及实际的私有数据。

MASCOT. 该协议表示了在SPDZ中使用带有恶意安全性[KOS16]的不经意传输(OT)计算Beaver triples的方法，这是SPDZ-2中发布的第一个离线阶段。这里的核心技术是使用带有恶意安全性的所谓OT扩展[KOS15]，这大大提高了吞吐量，因为公开密钥密码学只在计算的开始短暂地使用。

. MASCOT已经适应以2的幂为模计算[CDE+18, DEF+19]。这里的主要挑战是，并不是中的每个元素都有一个逆，这是证明MASCOT(和SPDZ)安全性的关键工具。通过移动到以获得更大的k'来抵消零因子的影响来缓解这一问题。MP-SPDZ完全实现使用自己的实现与编译时k优化。

SPDZ and Overdrive. LowGear和HighGear [KPR18]是两个协议的名称，它们分别使用半同态和somewhat同态加密为SPDZ计算Beaver三元组。他们是SPDZ-2的一部分。半同态是指可以通过加密文和乘密文，分别获得明文的和和乘积的加密。通过somewhat同态，我们的意思是，另外也可以将两个密文相乘，但结果不能再与一个密文相乘。所有已知的同态密码系统都会因每增加一级密文乘法而造成相当大的性能损失。SPDZ、LowGear和HighGear的核心思想是使用多方计算技术将这种乘法级别的数量最小化。LowGear和HighGear代表了一种权衡，因为LowGear在所有参与方之间运行子协议(类似于Bendlin等人[BDOZ11])，因此不能像HighGear那样根据参与方的数量进行扩展。由于MP-SPDZ不实现恶意安全的LowGear和HighGear所需的密钥生成，它们的变体使用表4中两个秘密安全协议的秘密安全密钥生成帐户。可以选择使用TopGear零知识证明[BCS19]来代替原来的变体。这减少了内存使用和较小计算所需的时间。

MP-SPDZ也保留了SPDZ协议早期变种的离线阶段，带有恶意的[DPSZ12]和隐蔽的安全性[DKL+13]。然而，由于它们被HighGear所取代，它们没有与在线阶段集成，因此没有出现在表4中。

Binary secret sharing. MP-SPDZ支持两种计算二进制电路的方法:秘密共享、不诚实多数和恶意安全。第一种方法是从中选取的，k = 1。然而，这种变体的缺点是通信在安全参数中是二次的。尽管这对于也是成立的，但是如果k大于安全参数，影响就小了，就像一样，因为基于不经意传输的协议的通信在中。

第二种是基于Frederiksen等人[FKOS15]对TinyOT的多方泛化，安全参数中通信是线性的。

BMR. Beaver等人[BMR90]提出了一种从继承安全特性的任何多方计算方案构造混淆电路的方法。他们的方法后来被Lindell等人改进[LPSY15]，使用SPDZ作为底层协议。MP-SPDZ利用SPDZ/MASCOT和其他安全模型中的协议实现BMR。这个功能从来都不是SPDZ-2的一部分，但在MP-SPDZ的第一个版本之前就部分发布了，因为Keller和Yanai使用它来实现无关RAM [KY18]。

 Yao’s Garbled Circuits. Bellare等人[BHKR13]提出了一种Yao的乱码电路的变体，它与AES-NI(现代处理器上AES的本地实现)工作得特别好。在SPDZ-2的最后一个版本之后增加了一个实现，最近扩展到包括半门技术[ZRE15]。

Semi-honest security. 将具有恶意安全性的协议转换为具有半诚实安全性的协议是相对直接的，方法是删除所有只对恶意安全性起作用的方面。SPDZ和TinyOT中的所有协议都具有实现这一点的两个主要元素:一个信息理论标签(在大多数文献中称为MAC)和一个称为sacrifice的过程，该过程使用更多的相关随机性来检查相关随机性的正确性。之后，后者不得不放弃，因为这一过程揭示了这两部分之间的关联，因此得名sacrifice。剥离两者后，协议将使用底层技术(无关传输或同态加密)，接近于规范的半诚实协议。主要的区别在于，在半诚实的设置中，人们可以直接使用OT或HE来处理秘密数据，而不是产生相关的随机性。然而，考虑到OT或HE的成本，与Beaver的乘法的额外成本相比，开销相对较小。此外，利用同态加密的相关随机性可以很容易地处理基于LWE的方案的SIMD结构，即这种方案只能一次加密数千个域元素，以获得合理的安全参数。这使得即使在计算顺序乘法时也可以使用单一加密。

因此，MP-SPDZ在所有计算域实现了一个基于OT的协议，以及半同态和somewhat同态加密域的协议。

3.2 Honest Majority

诚实-多数设置允许计算安全完全使用秘密共享，而没有不经意传输或同态加密。MP-SPDZ使用了两个秘密共享方案，replicated secret sharing[BL90]和Shamir的秘密共享[Sha79]。两者都是乘法，也就是说，可以在不进行通信的情况下本地计算两个共享的乘法共享，尽管会导致不同的秘密共享方案。涉及通信的重共享协议resharing protocol然后可以转换回原来的共享方案，从而促进进一步的倍增。resharing protocol是线性的，因为一个和的重新共享等价于重新共享的总和，这使得双方能够以一次乘法的通信成本计算内积。框架通过为内积提供特定的接口来反映这一点。

Semi-honest computation based on replicated secret sharing. Araki等人[AFL+16]观察到，通过使用伪随机零共享(CDI05)，可以由每一方发送恰好一个计算域元素来完成重新共享。后者是指在不通信的情况下，使用伪随机数生成并在每一对当事人之间共享一组密钥来生成一个新的零随机共享。Eerikson等人指出，一种类似的技术有助于减少私人输入的通信[EKO+20]。

Semi-honest computation based on Shamir’s secret sharing. 这可以追溯到Ben-Or等人[BGW88]计算素数模和Chaum等人[CCD88]计算特征二的扩展域(进而是二进制电路)。MP-SPDZ实现Cramer等人所描述的重共享[CDM00]。

Malicious computation. Lindell和Nof [LN17]已经将SPDZ sacrifice调整为一个质数的乘法秘密共享模的设置(包括replicated和Shamir的秘密共享)，Araki等人[FLNW17]已经为TinyOT这样做。这两部作品都是基于这样的观察，即使用同态加密或遗忘传输的optimistic triple production可以被使用乘法秘密共享的三元组乘积取代。这样的一对三元组就可以像在不诚实多数设置中那样进行检查，从而导致需要生产的三元组与在线阶段可用的三元组的比例。其中两个用于大型域(SPDZ)，三个用于基于位的协议(TinyOT)。

对于2的乘方计算，Eerikson等人[EKO+20]提出了几个变体，一个类似于TinyOT，另一个受sacrifice的启发，第三个基于通用编译器[DOS18]，第四个被称为post-sacrifice。最后一种方法是由Lindell和Nof [LN17]引入的，用于对一个质数取模的计算，它的工作原理是执行任何乘法，只使用半诚实的安全性，但存储输入和输出，以便稍后检查，使用与SPDZ sacrifice类似的随机三元组。这偏离了Beaver’的技术，并证明MP-SPDZ不限于它。

3.3 Higher-Level Protocols

上面描述的所有协议通常都与算术黑盒的实现有关，即私有输入、加法、乘法和公共输出。然而，许多计算，如比较，需要进一步的相关随机性，最明显的是秘密随机位在更大的领域。获取此类位的一种简单方法是拥有足够多的参与者(取决于安全模型)输入一个随机位，然后计算所有这些位的异或。然而，这并不能最优地伸缩到组方的数量，因为在更大的域中计算异或可简化为一个乘法:a⊕b = a + b−2ab。此外，对于恶意安全，它必须检查输出是否真的是一个位。

求一个素数的模，Damgard et al. (DKL + 13)表明，一个秘密随机位可以产生的成本只有一个乘法和一个开放使用的广场一个随机数没有透露这两个可能的根对应的(如果不是零)。Damgård等人[DEF+19]后来将其推广到对2的幂取模的计算。

Arithmetic-binary conversion. MP-SPDZ实现了算术运算(对较大的数取模)和二进制运算(对两个数取模)之间的几种转换方法。一般的方法是在两个领域中使用相关的随机性，即Rotaru和wood引入的所谓的doubly-authenticated bits双认证比特(daBits) [RW19]，以及Escudero等人引入的扩展的daBits [EGK+20]。在具有少量半诚实参与人的计算中，也有可能进行更直接的转换[ABF+18, MR18]。

3.4 Benchmarks

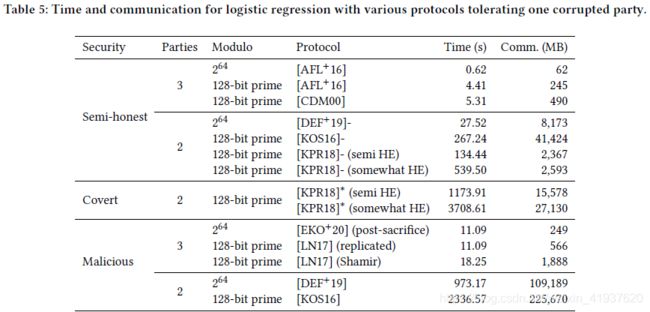
为了比较算术电路的协议，我们对10个特征的1280个示例和128批处理的逻辑回归的一个新纪元的计算进行了基准测试。由此产生的电路在1000多轮中进行了100多万次运算。表5和表6分别显示了我们在AWS c5.9xlarge实例上对一个和两个腐败的玩家的结果。注意，我们精确地计算sigmoid函数，不像ABY3 [MR18]。

对于计算二进制电路的协议，我们实现了计算由两个不同的32位方输入的向量的内积。表7和表8分别显示了我们在AWS c5.9xlarge实例上对一个和两个损坏的播放器的结果。注意，[CCD88]表示通过在特征二的域内嵌入位来计算二进制电路，以满足Shamir秘密共享的条件。此外，[LPSY15]之后的协议为BMR构造命名了底层协议。

4 INTERNAL INTERFACES

在基于秘密共享的多方计算中，并行通信在一定程度上是不可缺少的。这就提出了一个问题，即如何将该需求转换为一个尽可能容易使用的接口。考虑以下简单的操作符重载:

A = b * c

e = d * f

这两个乘法运算可以并行进行。然而，第一行隐含的通信必须至少延迟到第二行执行，这意味着a不能表示实际的共享，而是一个延迟的值，这反过来又要求后台有相当多的机器来处理通信和递延值的可用性。它的继任者VIFF [Gei07]就采用了这种方法MPyC [Sch20]和FRESCO [Ale20]。相比之下，MP-SPDZ的目标是在这个阶段提高效率，并将可用性推迟到更高的水平。因此，内部接口要求程序员指示并行计算。一个严格的基于矢量的接口是实现这一点的一种方法，但是MP-SPDZ提供了一个稍微更易于使用的变体。假设a和b是大小为n的倍数的向量，假设输出为c。

这个接口允许更动态的使用，而不需要首先将信息复制到向量中。

由于每个协议都提供相同的接口，因此使用c++模板一次性为多个协议实现相同的计算很简单，这也是因为输入和输出协议使用相同的方法。

回到我们的内积示例，图2显示了使用算术协议的内部接口实现的产品。当通信在交换调用中发生时，它将尽可能地并行化。此外，如果协议可用，代码将使用优化的点积工具。注意，所有协议的代码都是相同的。它只是输入、协议和输出对象的类型在协议之间发生变化。

4.1 Templating

c++模板在MP-SPDZ中被广泛使用，因为它允许在合适的时候重用代码，而不会造成性能损失。如果使用带有虚函数的运行时多态性，那么在协议不同的执行点上，每个附加的协议都会产生额外的开销。鉴于协议框架中实现不同的非常小的单位(例如,添加份额可以只涉及增加两个64位的数字,还增加了几个双数字模很大'),我们估计的成本运行时多态是相当大的,由于连续的分支。

作为模板好处的一个例子，Beaver的乘法[Bea92]的实现需要大约100行代码，同时被用于跨越所有计算域和多个安全模型的十多个协议。

任何协议的中心类都表示该协议中的一个秘密值。像对应的明文值和子协议的类型这样的其他所有东西都使用typedef从这个类派生出来。通常，描述特定协议的类有一个用于秘密值类的模板变量，所有派生信息都可以从这个模板变量中访问。

4.2 Preprocessing

后端相当大一部分用于所谓的预处理，这表示产生相关的随机性。这种随机性最突出的例子是乘法三元组([a]， [b]， [ab])，其中a和b是统一随机的，所有数字都是秘密共享的。这样的三元组是Beaver的乘法的核心。其他的例子包括平方(a, a^2)和逆(a, a^−1)，随机比特，daBits，和edaBits [EGK+20]。

MP-SPDZ提供了为半诚实和恶意安全性一般生成预处理的实现，以及特定协议的特定实现。例如，在SPDZ [DKL+13]中，不使用乘法而生成平方和更有效，或者在某些协议中，可以从随机比特生成二进制位，以2的幂取模。

由于批量生成预处理元素的边际成本更低，因此框架提供了这样做的基础设施。此外，还可以从磁盘读取这些信息，这有助于只对依赖于秘密数据的计算阶段(有时称为“在线阶段”)进行基准测试。

预处理通常是按需执行的，以避免不必要的计算，这与SCALE-MAMBA [COS19]不同，在SCALE-MAMBA [COS19]中，每当运行计算时，甚至会生成较少使用的平方。这不仅会减慢计算速度，还会导致应用程序在最后似乎挂起，因为预处理还没有完成。

5 THE VIRTUAL MACHINE

Keller等人[KSS13]提出了一个专门设计用于多方计算的虚拟机。这个虚拟机是MP-SPDZ的前身SPDZ-2 [KRSS18]的核心。虚拟机的主要特点是，涉及通信的指令允许不受限制的参数数量，从而减少通信轮数。正是这个特性使它区别于许多其他虚拟机和处理器。以64位x86指令集为例。虽然指令在完成所需的时钟周期数上有所不同(最小的是加法，但超过100个正弦或余弦[F+11])，但指令之间的差异很容易通过计算它们所需的二进制电路的差异来量化。在多方计算中，份额的增加和乘法不仅在数量上有差异，而且在质量上也有差异，因为前者可以在局部完成，而后者涉及通信。由于网络延迟，不同的协议之间存在质的差异，但是不受限制的通信并行化的好处是显而易见的。

在乱码电路的背景下，并行化特性还有另一个好处。Bellare等人[BHKR13]提出使用AES-NI实现乱码电路，AES的cpu本地实现。他们的方案利用了所谓的流水线，这意味着如果指令一个接一个地直接执行，那么多个AES操作可以在同一个CPU核心上并行运行。虚拟机设计允许利用流水线，同时在这方面减轻了用户的负担。

High-level design. SPDZ-2实现了SPDZ在线阶段，用于Fp中一个大素数p和n = 40或n = 128的的计算。MP-SPDZ增加了一系列协议，一些协议用代替，并增加了布尔电路的计算(技术上是)。后者根植于Keller和Yanai [KY18]所使用的实现，默认情况下它使用长度为64的向量。对于一些共享只包含一个位或一对位的协议来说，这对于效率是必要的，通过使用当代处理器的64位机器字，同时计算64位操作，这将导致自然的优化。因此，虚拟机的每个实例都提供了类似整数的计算(在或中)，以及和布尔电路的计算，所有这些都在相同的安全模型中。

Basic data types. 虚拟机允许为每个计算域和64位整数处理公共和秘密值的数据。在每个域中在另一个整数类型之上有明确的数据类型的原因是计算域中数字的大小不同，并且Fp中的数字使用Montgomery表示存储，它不适合用于循环计数器或寻址内存等目的。因此，使用反映所有计算域的公共数据类型更简洁。此外，在乱码电路的上下文中，在乱码之前已知的公共号码(如循环计数器)和来自揭示秘密值的数字之间存在概念上的差异。这个差异很重要，因为计算的乱码部分依赖于显示值，必须在计算结果产生上述值之后发生，而乱码只依赖于循环计数器，可以在任何时候处理。

Registers. 虚拟机为每种基本数据类型提供无限数量的寄存器。虽然这没有基于堆栈的设计复杂，但它允许更简单的实现。寄存器号被硬编码到字节码中，这使得虚拟机能够为计算分配足够的数字。寄存器通常用于存储指令的输入和输出，并且它们是线程本地的。

Memory. 对于更复杂的数据结构，如数组、矩阵和高维结构，虚拟机为每一种基本数据类型提供另一种工具，称为内存。内存数组是全局的，因此允许线程之间通信信息。与寄存器不同，可以使用存储在整数寄存器中的运行时值访问内存。内存必须在编译时分配。

Instructions. 虚拟机支持的大部分指令大致可以分为以下几类:

Copying  这包括初始化寄存器、在寄存器和内存之间复制，以及不同公共数据类型的寄存器之间的转换。

Simple computation  类似于常见的三参数格式的指令用于所有不需要通信的计算，包括对秘密值的线性操作。

Secure protocols  所有这类指令允许无限数量的论据，以促进减少沟通轮如上所述。
这些协议包括必要的，如私有输入、乘法和公共输出，但也包括更专门的，如内积、矩阵乘法、2D卷积和Dalskov等人的特殊截断[DEK19]。

Preprocessed information  如第4.2节所述，预处理是成批执行的。这意味着这种类型的指令只会在必要时发生通信。为了优化预处理，还可以通信磁带中所需的预处理信息量。

Control flow  虚拟机允许跳转、衍生和连接线程。

Further input/output  这类指令促进了安全协议之外的功能，如打印或客户端通信。

Protocol information  我们可以通过访问玩家数量等信息在不同玩家配置中使用相同的程序，然后在收集输入时循环遍历所有可用玩家。

Vectorization. 大多数指令都是向量化的，也就是说，它们意味着对请求的多个连续寄存器执行相同的操作。这大大减少了在编译和执行期间表示重复计算的开销。虚拟机还有助于结构化地将值加载到连续寄存器中，例如，加载多维数组中任意维度的行。

Threads. 虚拟机实现多线程的方法如下:计算在主线程中运行，这一过程由称为“tape”的指令列表描述。后者可以在其他线程中启动更多的tape，并等待它们完成。但是，必须在编译时知道线程的最大数量。尽管有这个限制，但是可用的功能对于许多从多线程(如矩阵乘法或卷积)中获益的应用程序来说已经足够强大了。

Inner product example. 图3显示了长度为3的向量的内积示例的字节码表示。注意，inputmixed, dotprods, asm_open都将参数的数量作为第一个参数。第一个指令允许分别将参与方0和1的私有输入存储在寄存器s1、s3、s5和s2、s4、s6中，然后将内积的结果存储在s0中。最后，显示内部产品并打印，后面跟着一个新的行字符。

6 THE COMPILER

与SPDZ-2类似，编译器运行用Python编写的高级代码，并输出由虚拟机运行的字节码。
正如本章所指出的，有些方面已经更改。然而，以下核心方面保持不变。

Type system.  MP-SPDZ遵循Python的动态类型范式。这使得编程更加直观，例如，任何涉及秘密值和公共值的操作都会产生秘密值。考虑在一个更强的类型系统中，将秘密类型赋值给公共类型将涉及自动揭示，这可能是无意的，或者编译器将需要产生错误，这将使编程更加困难。因此，动态类型加上一个明确命名的方式来揭示秘密信息，就在安全性和易用性之间找到了折衷。

Basic blocks. 这个概念来源于一般的编译器设计，表示没有分支的指令序列。编译器只在基本块的上下文中执行最小化循环的优化，因为它需要重新安排指令。

6.1 Minimizing the Number of Rounds

这是编译器进行的主要优化。它分析一个基本块，找出可以合并成一条指令的同类指令，因为它们是独立的。回想一下，这样的指令允许无限个参数。合并的一个简单例子是可以并行运行的两个乘法。MP-SPDZ与SPDZ-2的不同之处是，它独立地合并不同的操作，而SPDZ-2使用海狸乘法减少了对开口的乘法。这样的缩减显然排除了不使用Beaver乘法的协议。因此，MP-SPDZ使用安全乘法指令，该指令独立于开放操作进行合并。与SPDZ-2的另一个区别是，后者将打开过程分成两个指令，分别称为startopen和stopopen，这使得在等待来自网络的信息的同时执行本地计算。然而，这是以增加编译器的复杂性为代价的，而且并行打开的数量受到通信缓冲区的限制，这必须在编译器级别上考虑。MP-SPDZ使用单一指令进行打开，简化了处理。

该算法分为三个步骤:

1. 首先，它创建一个基本块中所有指令的依赖图。这个图采用有向无环图的形式，其中节点代表指令。在两个节点之间创建一条边有几个原因，最明显的是如果一个指令的输出是另一个指令的输入。其他依赖包括与环境的各种类型的交互，例如，从一方读取输入的顺序不应该改变。
2. 该算法分配的指令可以合并为轮。同一回合的所有指令都具有相同的类型。这是通过最长路径算法的变体来实现的: (a)所有没有前辈的节点取四舍五入；
   (b)每个不可合并的节点都被赋值为其前一个节点的整数的最大值；
   (c)每个可合并节点都被分配比其所有前一个节点都大且相容的最小轮数，即它不被另一种类型的指令占用。由于该算法只考虑节点的前身，它可以与依赖图的创建一起运行。
3. 所有指令在同一轮合并。这包括合并参数以保留语义，以及合并依赖关系图中的所有边。
4. 指令根据更改后的依赖关系图按拓扑顺序输出。

内存指令依赖。 由于内存指令允许运行时地址，所以在依赖关系图中如何处理它们并不简单。如果每个读指令都依赖于一个写指令，反之亦然，那么可能会丢失很大的最小化轮数的潜力。考虑一个展开循环，其中读取一个内存地址，然后对读值进行一些计算，结果存储在相同的地址，并对更多的地址重复相同的操作。所有的计算都可以并行执行，但是由于每个内存指令都依赖于前一条指令，所以无法并行执行。因此，编译器只考虑涉及相同地址的依赖关系，无论是编译时地址还是运行时地址的相同寄存器。在访问数据结构(如多维数组)时结合缓存寄存器，可以在效率和正确性保证之间取得平衡。此外，编译器提供了一个命令来启动一个新的基本块，这从本质上保留了指令的顺序。

Dead code elimination. 上面创建的依赖关系图还允许消除带有未使用结果的指令。如果一个指令不被认为是本质上必不可少的(因为对环境或内存的副作用)，并且所有的后继指令都被淘汰，那么它就被认为是过时的。一个简单的向后传递就足以确定和消除过时的指令。

6.2 Register Allocation  寄存器分配

与SPDZ-2中一样，编译器最初使用无限的write-once寄存器，最后将这些寄存器分配给最小数量的寄存器。对于一个没有分支的直线程序，通过向后传递，在最后一次读取时分配寄存器，在写入时释放寄存器，这是很简单的。对于一个有分支的程序来说，有些寄存器必须在整个循环中存在，以防止在最后一次读取后重写，这是很困难的。这可以通过分配寄存器来解决，这些寄存器是在循环开始之前写入的，在处理循环的各个部分之前。

6.3 Loops

虽然多方计算的本质使实现依赖于秘密数据的循环变得非常重要，但依赖于公共数据的循环自然减少了计算的表示。与SPDZ-2类似，MP-SPDZ支持依赖于编译时和运行时公共数据的循环。前者仍然允许对计算代价进行编译时分析。在高级语言中，可以使用函数装饰器执行循环:

虽然这很不寻常，但它通过在编译器范围内运行高级Python代码来实现编译。此外，它允许在不创建特定于领域的语言的情况下进行各种循环。例如，@for_range创建连续执行的严格运行时循环，@for_range_opt实现下面描述的动态优化，而@for_range_multithread和@for_range_opt_multithread在固定数量的线程中执行循环。

Dynamic loop optimization. Büscher等人[BDK+18]描述了在第6.1节中为了合并通信轮而展开的循环和在编译期间由于表示展开计算而增加的空间而限制内存使用之间的权衡。他们提出一种动态的方法，直到时间预算耗尽为止。MP-SPDZ通过使用生成指令数的预算来调整他们的方法，这可以作为总体编译成本的代理。

6.4 Repetitive Code

由于多方计算中的基本计算仅限于一个域内的加法和乘法，因此即使是看似简单的计算，如比较，也会转化为基本运算的非平凡组合。MP-SPDZ的设计原则是将计算分解为基本运算，以限制虚拟机的复杂性。然而，这意味着重复的代码会导致相同构建块的重复扩展。为了避免这个代价，编译器提供了像6.1节中那样原子地处理一些基本计算并合并它们。在加快编译速度的同时，这样做的缺点是一些并行计算将顺序执行。例如，对独立数据的比较和相等测试可以并行执行(从而减少轮数)，但是分开处理这两个测试将依次执行它们。由于折衷的原因，此优化只在请求时使用。

以上述方式处理的构建块实例范围从整数操作(如比较和截断)到数学函数(如三角函数)。

作为一个具体的例子，考虑计算几个值的最大值的情况。为了最小化轮复杂度，这必须以二叉树的形式计算，在每个节点上选择最大值，并且在每个级别上的所有比较都应该并行计算。以向量化的方式进行编程有点麻烦。MP-SPDZ允许使用简单的递归方法，合并所有并行比较。通过重复的代码优化，这在创建用于比较的电路之前发生，这大大加快了编译速度。

7 HIGH-LEVEL LIBRARY

在本节中，我们将描述在编译器上实现的秘密计算的能力。这些实现通常涉及到将所需的功能分解为协议支持的基本操作，如计算域中的输入、输出和算术。由于这些操作是由算术黑盒建模的，因此通常可以直接证明扩展功能的安全性。

7.1 Integer Operations

补充比较，相等，左/右移位，2的模幂，2的幂有秘密指数。在较大的计算域中，大多数这些操作的核心组件是“mask-and-open”方法。这涉及到将某种形式的秘密随机值与秘密值相加或相减，并打开结果，然后可以将结果作为公共值处理，例如提取单个位。图4给出了位分解的基本示例。它使用这些公开位与屏蔽的秘密位一起计算一个秘密值的位分解，也就是说，对每个位共享一个单独的秘密，而不是对整个值共享一个秘密。与后者不同，前者允许直接计算上述所有整数运算。Catrina和de Hoogh [Cd10]演示了如何利用质数的计算模来优化这个简单的方法，后来Dalskov等人[DEK19]对2的幂的计算模进行了改进，Escudero等人[EGK+20]对其部分转换为二进制计算。

Mask-and-open对素数的计算取模只在统计上是安全的，并且要求秘密值在一个假定的间隔内。例如，假设，对于安全参数s，随机选择，则x + r在统计上与中的均匀数没有区别。在对2的幂取模的计算中，这不是问题，因为溢出位可以简单地通过与2的幂相乘来“擦除”。

7.2 Fractional Numbers

作为SPDZ-2, MP-SPDZ提供了两种表示小数的方法:定点和浮点。前者用整数y表示一个分数x，使表示固定精度f。后者类似于IEEE 754等浮点表示，x由四元组表示
这样

附加位s和z简化了计算，因为安全计算不直接允许访问较大值的单个位。

Fixed-point numbers. 由于效率较高，这是MP-SPDZ中用于小数的首选方法。加法和减法是直接的线性表示，乘法对应整数乘法，然后截断f位。截断既可以计算为左移，也可以计算为更有效的概率截断。后者涉及基于输入的随机舍入。例如，当四舍五入为整数时，0.25将四舍五入为0，概率是0.75，而四舍五入为1，概率是0.25。Catrina和Saxena首先提出这一方法用于质数模计算[CS10]， Dalskov等[DEK19]将其用于2的幂模计算，Escudero等[EGK+20]用于混合计算。katrina和Saxena还提出了如何使用Goldschmidt算法[Gol64]在安全计算中计算除法。

Floating-point numbers. Aliasgari等人[ABZS13]演示了如何在素数取模的安全计算环境中实现浮点数。他们的方法直接转化为Z2k，除了乘以来计算x在时的左移。然而，这可以通过位分解来实现。标准库实现浮点数的加减除法和比较。请注意，Aliasgari等人的方法并不完全符合IEEE754。然而，在SCALE-MAMBA [COS19]提供的Bristol Fashion格式中，可以使用二进制电路进行一些运算(加法、乘法、除法和平方根)的兼容计算。参见7.3节。

Mathematical functions.  Aly和Smart [AS19]已经在安全计算中实现了许多数学函数，范围从平方根的三角函数到指数和对数。MP-SPDZ通过重用作者通过SCALE-MAMBA [COS19]提供的代码集成了这一点。所有函数都是为定点数实现的，而浮点数的实现被限制为正弦、余弦和正切。

7.3 Further Functionality

该库扩展了基础数学，如下面的段落所示。

Machine learning. 该库提供了逻辑回归[KS19]和深度学习推理[DEK19]的功能。前者允许在sigmoid函数的精确实现和近似于ABY3 [MR18]之间进行选择。后者支持在MobileNets [JKC+17]和一些ImageNet解决方案中使用的量化方案，如DenseNet、ResNet和SqueezeNet。这些是在CrypTFlow [KRC+20]的帮助下从TensorFlow自动编译的，这为进一步使用网络打开了可能性。

Oblivious data structures. MP-SPDZ保留Keller和Scholl使用的代码[KS14]。这包括一个无关数组、队列和堆栈实现。在这里，Oblivious的意思是所有访问都是秘密进行的，也就是说，没有显示索引(如果适用的话)以及访问是读还是写。然而，它是固有的安全计算，在结构中的数据量的上限被揭示。无关RAM [SvS+13]是实现更大尺寸的高效数据结构的核心技术。基于上述数据结构，库中包含了图中最短路径的Dijkstra算法和稳定匹配的Gale-Shapley算法的示例实现。

Binary circuits. 该库允许以所谓的布里斯托时尚格式处理二进制电路。这种基于文本的格式是由SCALE-MAMBA [COS19]的作者建立的，其灵感来自于用于其他安全计算框架的类似格式。SCALE-MAMBA带来了一个选择的示例电路，如Keccak海绵功能[BDPVA09]。在后者的基础上，该库提供了短输入的SHA3计算。MP-SPDZ与SCALE-MAMBA不同，MP-SPDZ在编译器中对二进制电路进行处理，以优化它们的秘密共享计算和姚的乱码电路。SCALE-MAMBA只在bmr风格的乱码电路中使用布里斯托时尚电路，这样的优化作用较小，因为在AES中使用的密钥是不固定的。