Swift 与 OC 枚举的异同
Swift 与 OC 枚举存在的不同问题与解决方案。
OC 中枚举的问题
在C、C++、Objective-C这类语言中,枚举实际上是整型的别名,仅具备整型的能力,由于类似的语言的类型系统很弱,以至于无法发现一些潜在的错误。
比如在OC中可以定义一个方向的枚举:
typedef NS_ENUM(NSUInteger, Direction) {
EAST,
SOUTH,
WEST,
NORTH
};在使用的时候,通常会使用if或switch语句:
if (direction == EAST) { // do something
}有时会出现这样的代码:
if (direction == 0) {
// do something
}类型系统并不会发现问题,因为枚举就是整型,但是当枚举的定义发生变化时,这样的代码就变成了bug,而且很难排查。
此外,在逻辑上,完全可以写出EAST + SOUTH这样的代码,由于方向不具备可加性,这样的代码毫无意义,对于这样的代码,OC的类型系统并不会报错。
Swift 中的枚举
Swift中的枚举变成了一个独立的类型,这意味着,当我们在Swift中同样的定义:
enum Direction {
EAST,
SOUTH,
WEST,
NORTH
};这几个值并非0,1,2,3(当然也可以让他们恰好等于这些值)。
Swift为枚举提供了远超整型的能力,除了基本的if和switch模式匹配等基本用法之外,还可以:
指定成员的类型,如Int、String以及任意的类型
定义方法和计算属性
获取枚举所有成员的数组,Direction.allCases.
关联值,可以使用元组来存储数据,配合模式匹配可以大幅减少代码,并且支持泛型关联值。
作为一个类型,可以实现协议,定义扩展
实现递归枚举,可以很方便的表示类似列表或者树的结构,配合递归函数降低理解成本。
这些特性官方文档都有详细的说明,这里就不展开了。
Swift中的枚举和OC枚举的相同之处就是名称一样,内涵和外延已经完全不同,其核心价值在于提供了在多种类型(而非仅仅整型)间做选择的机制,在将这种机制的实现细节与对外抽象分离的同时,赋予其上述所有的能力,这提供了更高的抽象层次和更强的表现能力。
接下来我们来看一个简单的例子和一个综合应用的例子。
牛刀小试——简化错误处理
之前,函数的正常结果和异常结果是无法统一的,体现在代码上往往以类似if(someValue !=nil) {} else {}的方式来处理,有了枚举之后,可以利用Optional将两种结果进行抽象统一,从而简化错误流程。下面这个例子的作用是从一个json字符串实例化为模型对象:
正常的代码:
func makeModel1(s : String?) -> Model?
{
let d1 = s?.data(using: String.Encoding.utf8)
// 判断是否为空
if let a = d1 {
// 可能throw的代码try一下
guard let dict = try? JSONSerialization.jsonObject(with: a) as? Dictionary else {
fatalError("Json data error")
}
let model = Model.init(dict: dict)
return model
}
return nil
} 利用Optional简化后的代码
func makeModel2(s : String?) -> Model?
{
s?.data(using: String.Encoding.utf8).map{
try? JSONSerialization.jsonObject(with: $0)
}.map {
Model.init(dict: $0 as! Dictionary)
}
} 这个逻辑并不复杂,但还是足以显示出合理抽象的威力,Optional提供了这样一种抽象,将错误处理的细节屏蔽掉了,我们只需要写数据转换的主逻辑,这种写与读的顺畅性在带给我们愉悦的同时,也提升了程序的正确性。在实际场景会遇到更复杂的多层嵌套各种if的代码,主流程非常不清晰,各种错误处理很容易出错,这个时候非常适合用Optional来简化。第二个版本是为了优化了可读性故意变成了多行,实际上只有一行代码
func makeModel2(s : String?) -> Model?
{
s?.data(using: String.Encoding.utf8).map{try? JSONSerialization.jsonObject(with: $0)}.map { Model.init(dict: $0 as! Dictionary)}
} 综合应用——关联值、递归、模式匹配、方法定义、与高阶函数结合
在swift中,枚举有几个新的能力,比如可以关联值,支持递归,进行模式匹配,定义方法,正是这些能力使得枚举实现了能力的进击,我们通过一个例子来展示一下这些特性如何让我们的表达更方便。
最近笔者在设计一个表达式引擎的方案,在一开始研究了一个非常简单的表达式系统,即有理数域的加减乘除,这里笔者组合了模式匹配、关联值、方法定义、递归枚举的能力,用很少的代码进行了抽象,并将这个四则运算的表达式系统用于计算经典的游戏算法——24点,24点的游戏抽象成算法问题是这样的:
给定任意4个1-10内的整数,计算出它们都过加减乘除得出24的所有表达式在继续往下之前,读者可以思考一下使用OC应该如何解决。
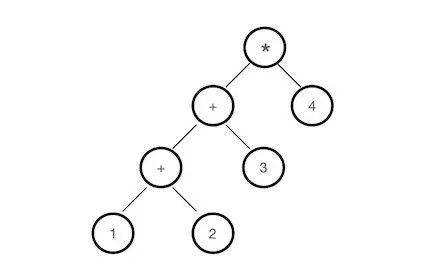
接下来我们开始,假如4个数字是1,2,3,4,我们知道(1+2+3)*4=24,考察(1+2+3)*4,这个可以看成一个如图所示的运算
这张图很直观的体现了3个信息:
表达式可以体现为树的形式,而树是很适合用递归来描述的;
表达式的节点分为两种,一种是数字,一种是运算,并且每个运算必定关联两个节点
表达式的求值过程式是递归地将运算应用到两个节点的过程
因此我们可以利用枚举关联值、递归的能力建立表达式的模型,并且利用模式匹配定义求值的方法:
enum Exp {
case value(Double) //值节点
indirect case plu(Exp, Exp) //加法
indirect case sub(Exp, Exp) //减法
indirect case mul(Exp, Exp) //乘法
indirect case div(Exp, Exp) //除法
// 求值,模式匹配
func eval() -> Double {
switch self {
case .value(let value):
return value;
case .plu(let exp1, let exp2):
return exp1.eval() + exp2.eval()
case .sub(let exp1, let exp2):
return exp1.eval() - exp2.eval()
case .mul(let exp1, let exp2):
return exp1.eval() * exp2.eval()
case .div(let exp1, let exp2):
return exp1.eval() / exp2.eval()
}
}
}一个四则运算表达式的建模和求值就完成了。如果是利用class定义,需要定义一个类似Type的枚举来表示加减乘除,这就需要多写很多代码,更重要的是,加减乘除和具体的Double值之间的处理会比较繁琐,而对于枚举来说,就像呼吸一样自然。
那么怎么用这个Exp的枚举解决24点问题呢,这里一共有两大步:
将4个数字表示为可能的表达式数组,这一步又分成两小步:
获取4个数字的全排列
针对每一种排列方式,在每两个相邻的数字中间插入不同的运算符号
对数组中的表达式求值,取其中结果为24的表达式
限于篇幅,这里直接给出代码和注释
// 查找4个数字的24点答案
func search24(_ nums:(Double, Double, Double, Double)) -> [Exp] {
return makeExpFromNums([nums.0,nums.1,nums.2,nums.3]).filter{ $0.eval() == 24}
}
// 将一个数组递归构造成Exp的数组
func makeExpFromNums(_ nums:[Double]) -> [Exp] {
if (nums.count == 0) { //返回空数组
return []
} else if (nums.count == 1) { // 返回值
return [.value(nums.first!)]
} else { // 1、排列,2、分割数组,3、对分割后的两部分递归构造Exp,4、对递归的两个Exp数组组装成最终的Exp数组
return permutation(nums).flatMap{partition($0).flatMap{makeExpFromExpArray((makeExpFromNums($0.0), makeExpFromNums($0.1)))}}
}
}
// 构造4个数字的全排列,这是个递归函数,将第一个元素插入到后续元素的全排列中即可
func permutation(_ nums:[Double]) -> [[Double]] {
if (nums.count == 0) {
return [[]]
}
return permutation(Array(nums.suffix(from: 1))).flatMap{insert(num: nums.first!, nums: $0)}
}
// 给点一个数组nums,有nums.count+1的插入点
func insert(num:Double, nums:[Double]) -> [[Double]] {
(0...nums.count).map{nums.prefix(upTo:$0) + [num] + nums.suffix(from:$0)}
}
// 将一个数组分割成两部分
func partition(_ nums:[Double]) -> [([Double], [Double])] {
(0...nums.count).map{(Array(nums.prefix(upTo: $0)), Array(nums.suffix(from:$0)))}.filter{$0.0.count != 0 && $0.1.count != 0}
}
// 两个Exp的数组,双重循环构造Exp数组
func makeExpFromExpArray(_ exps:([Exp], [Exp])) -> [Exp] {
exps.0.flatMap { exp1 in
exps.1.flatMap{ exp2 in
[.plu(exp1, exp2), .sub(exp1, exp2), .mul(exp1, exp2), .div(exp1, exp2)]}
}
} 怎么样,是不是很简单,有了第一部分的抽象,第二部分代码除了递归的终止条件之外,都只有一行代码,这部分代码也展现了枚举与函数式编程结合后对于计算强大的抽象和表达能力。
有兴趣的读者可以尝试用OC实现一下同样的功能,然后对比一下代码。
Swift 中枚举的本质
除了官方文档和上面的两个例子之外,我们来聊聊枚举类型的本质,这里并不是去探究其底层实现,而是逻辑上应该如何理解枚举,以及什么情况下应该使用枚举。
对于类和结构体来说,我们可以定义多个属性,在一个实例中,这些属性的值是同时存在的,这就相当于多个值的与,逻辑上等价于数学上集合间的笛卡尔积,因此这两种被称为积类型。
对于枚举来说,无论我们定义多少个值,在一个实例中,只能存在一个,这就相当于多个值的或,逻辑上等价于数学上集合间的不相交并集,因此枚举被称为和类型。进一步说,Swift的枚举可以定义初始化器、方法和属性、遵循协议,其成员可以有关联值,基本上与类和结构体的能力对齐,这是因为枚举是积类型的对偶,也叫余积类型。
因此,可以得出使用枚举的充要条件,当取多个选项中的一个选项时,应该使用枚举,反之亦然,枚举适用于在多种情况下选择其一的场景,这样,就不会出现在一个类型中同时定义数据和errorCode的情况了。
在现代语言中,和类型的使用越来越多,最典型的就是是可空类型,Scala中的Option,Kotlin中的可空类型,Haskell中的Maybe。除了Optional,Swift系统库中的Result、Change都是枚举,包括Combine框架也大量应用了枚举。
✿ 拓展阅读
作者|四点
编辑|橙子君
出品|阿里巴巴新零售淘系技术