ML/DL题（一）-漫谈距离美

———–题目不是用来刷的，是用来思考的！—————

目录

题目
1.1 欧式距离
1.2 曼哈顿距离
——————————-思考——高手的分割线———————————–

1. 距离的美学
2. 样本相似性度量
   2.1 闵氏距离
   2.1.1 曼哈顿距离/绝对值距离
   2.1.2 欧几里得距离
   2.1.3 切比雪夫距离
   2.1.4 闵氏距离的共同点
   2.2 马氏距离
   2.3 从概率角度看马氏/欧式距离
   2.4 杰卡德相似系数
3. 变量间的相似度度量
   3.1 相关系数
   3.2 余弦相似度
4. 两个概率分布间的相似度度量
   4.1 从极大似然估计谈到KL散度
   4.2 巴氏距离
5. 对信息的相似度度量
6. 类，群或社区间的相似性度量
7. 我眼中的距离到底有多美

前言

对于学生而言，除了参加竞赛，另一个能增强自己实力的方法就是刷题。为什么刷题能起那么大的用处，我也是听到了coursera上learning how to learn的老师讲了之后才宛然大悟的，虽是数学系的学生，但自己平时做的题确实是很少。所以从今天开始，争取每天整几道关于机器学习，深度学习的面试题，从面试题中整理知识，同时看一下每个考点都是怎么在实际工程中应用的，以及它和其他相关联的知识点之间的关系是什么？

今天是第一篇，看一下距离的考点。

1. 题目

在k近邻或knn中，我们常用欧式距离来计算最近的邻居之间的距离，有时也用曼哈顿距离，请说说他们之间的差别？

答：

1.1 欧式距离

（1）欧式距离是由闵氏距离的参数q取2的时候推导出来的，比如计算点 x=(x1,x2,⋯,xn),y=(y1,y2,⋯,yn) 的欧式距离可以表示为：

d(x,y)=∑i=1n(xi−yi)2‾‾‾‾‾‾‾‾‾‾‾‾⎷

既然是由闵氏距离推出来的，那它也就有闵氏距离的两个缺点：

• 缺点1:要求计算距离的指标必须处于同一量纲下。但我们可以对各个指标进行标准化，使其转换为同一分布

• 缺点2:欧式距离要求各个坐标对距离的贡献应该是相同的，且变差相同。（一个坐标轴就表示一个变量，变差表示一个变量两个不同取值的偏差）
  解决方法就是 对欧式距离公式进行一定的改写：

  d2(xik,xjk)=[∑k=1p（xik−xjkskk）2]12
  其中 skk 表示变量k的标准差,就是把分布都标准化到均值为0，方差为1的标准正态分布。

1.2 曼哈顿距离

曼哈顿距离又称为城市区块距离，是在欧几里得空间中的固定直角坐标系上的两点所形成的线段对坐标轴的投影之和。如图所示：

如图所示，红线，蓝线，黄线均为曼哈顿距离 =12，绿色为欧几里得距离= 6X2‾‾√=8.48
之所以又称为城市区块距离，是因为从一个十字路口转到下一个十字路口，走的就是曼哈顿距离，如果你能穿越大楼，沿着直线走就是欧几里得距离。

——————————-思考——高手的分割线———————————–

1.距离的美学

最常见的应该就是欧式距离了，查看维基百科，可以发现欧式距离定义为在欧几里得空间中两点间的普通距离。注意最关键的是两点间的距离，也就是说只要计算欧几里得距离，就一定存在两点，你可能会说，这不是废话吗？

请问你怎么定义两点？
我是数学系的，学数学的人应该都知道，数学是对这个世界的高度抽象。如果从你问一个数学老师，什么是无穷大，老师展示不出来给你，如果你问他，那我能不能看一下点，数学老师可能也拿不出一个点给你看。因为那是抽象出来的，在大尺度上，人可以是一个点，在纸上用笔点一下，也是一个点，你可以把一栋楼，一个城市，甚至一个国家看成点，关键在于你怎么看待它。
这有个视频，看完你会更理解我想表达的是什么？点我：powers of ten

我在说什么？既然什么东西都能看成是一个点，那我就把距离抽象为两个东西的相互作用的关系，这两个东西你可以认为它是两个点，两个向量，两个分布，那距离就更广泛了，我一起来看一下一般公认的距离都有什么？怎么定义的！

2. 样本相似性度量

2.1 闵氏距离

要用数量化的方法对事物进行分类，就要用数量化的方法来定义每个样本的相似程度，这个相似程度在数学上可以用距离来衡量，最常用的闵氏距离：

dp(x,y)=[∑k=1p|xk−yk|q]1q

事实上，这是一种距离的定义，当q取不同的取值的时候，可以得到不同的距离公式。

2.1.1 曼哈顿距离/绝对值距离

当q=1时，可以得到曼哈顿距离。

d1(x,y)=[∑k=1p|xk−yk|](1)

前面已经有对于该距离的定义了，这是它的数学表达式。

from scipy.spatial.distance import _validate_vector
def cityBlock(u,v):
    u = _validate_vector(u)
    v = _validate_vector(v)
    return abs(u-v).sum()

2.1.2 欧几里得距离

当q=2时可以得到欧几里得距离：

d2(x,y)=[∑k=1p|xk−yk|2]12(2)

from scipy.spatial.distance import _validate_vector
from numpy import linalg as LA
def euclidean(u,v):
    u = _validate_vector(u)
    v = _validate_vector(v)
    return LA.norm(u-v)

这样也可以：

def euclidean(u,v):
    u = _validate_vector(u)
    v = _validate_vector(v)
    s = abs(u-v)**2
    s = s.sum()
    return np.sqrt(s)

欧几里得距离前面也仔细说了，这就不细说了。

2.1.3 切比雪夫距离

当 q=∞ 时，可以得到切比雪夫距离：

d∞(x,y)=max1≤k≤p|xk−yk|(3)

证明方法适用夹逼定理即可。

def chebyshev(u,v):
    u = _validate_vector(u)
    v = _validate_vector(v)
    return max(abs(u-v))

其中最常用的又是欧式距离，因为当坐标轴进行正交旋转的时候，欧式距离是保持不变的，而很多算法，都是需要变换坐标轴的。

2.1.4 闵氏距离的共同点

既然这三种距离都是由闵氏距离推导出来的，因此他们都具有相同的缺点，如下：
- 缺点1：闵氏距离没有考虑样本的各指标的数量级水平。当样本的各指标数量级相差悬殊时，该距离不合适。
- 解决方法：在计算距离之前，先把所有指标都转化为统一的分布内，即标准化。

• 缺点2:使用欧式距离要求各坐标对距离的贡献应该是同等的，且变差大小也是相同的，如果变差不同，则不太适用。
  比如在择偶时衡量一个男性的指标，假如是身高和收入水平，一个人是1.5米，收入6000，另一个人是1.8米，收入5500，这两个人的两个指标的变差差别就很大，不好用欧式距离。

• 解决方法2:将欧式距离进行一定的改写：

  d2(xik,xjk)=[∑k=1p（xik−xjkskk）2]12
  其中 skk 表示变量k的标准差，其实就是为了调整变量的变差。

2.2 马氏距离

与闵氏距离相似的还有马氏距离，它是对闵氏距离的进一步调优,向量 xi,xj 的马氏距离定义为：

dij(M)=(Xi−Xj)Tϵ−1(Xi−Xj)‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√

其中 ϵ−1 表示协方差矩阵的逆，协方差阵定义如下：

该距离可以表示数据的协方差距离，能非常有效得计算两个未知样本集的相似度。
若协方差阵为单位矩阵，则该距离就是欧式距离，如果协方差阵为对角阵，则该距离为优化后的欧式距离：

d2(xik,xjk)=[∑k=1p（xik−xjkskk）2]12=[∑k=1p(xik−xjk）2s2kk]12

s2kk 表示方差。

可以证明它对一切线性变换是不变的，故不受量纲的影响，它不仅对自身的变差做了调整，还对指标的相关性也做了考虑，非常适用于两个未知样本集的相似度计算。

2.3 从概率角度看马氏/欧式距离

设有两个一维正太分布 G1:N(μ1,σ21)和G2:N(μ2,σ22) ,若有一个样本位于A处，如下图所示：

从绝对距离看，点A距离左边的分布 G1 貌似更近一点，即 |A−μ1|<|A−μ2| ,但是从概率的角度，这个就未必了。
学过概率的人应该都知道，样本在每一段的概率是固定的，和方差 σ 有关，如图所示：

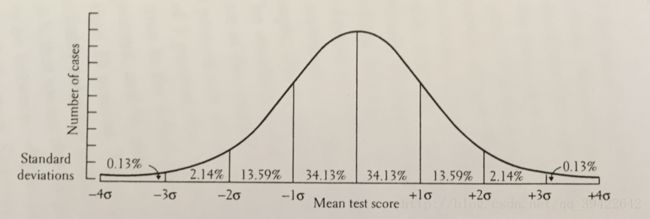
由他们的图像可以推断点A大致位于 G1 右侧的 2σ 左右，而位于 G2 左边的 σ 左右，因此从概率的角度来看点A要离 σ 更近。

2.4 杰卡德相似系数

杰卡德相似系数(Jaccard similarity coefficient) 是用来衡量两个集合A，B在A，B的并集中所占的比例，称为两个集合的杰卡德相似系数，定义如下：

J(A,B)=A⋂BA⋃B

因此，杰卡德相似系数可以用来衡量两个样本的相似性。

与之相反的是杰卡德距离，定义如下：

它是用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。

举个例子：样本A与样本B都是n维向量，并且所有维度的取值都是0,1。例如A(0011),B(1110),我们可以将样本看成是一个集合，1表示集合包含该元素，0表示集合不包含该元素。因此有：

• M11：样本A，B都是1的维度个数
• M01：样本A是0，样本B是1的维度个数
• M10：样本A是1，样本B是0的维度个数
• M00：样本A，B都是0的维度个数

根据定义，杰卡德相似系数可以表示为：

J=M11M01+M10+M11

即 M01+M10+M11 表示并集的元素个数， M11 表示交集的元素个数。

相应的杰卡德距离定义为：

DJ=M01+M10M01+M10+M11

杰卡德距离的python代码如下：

def jaccard(u,v):
    u = _validate_vector(u)
    v = _validate_vector(v)
    dist = (np.double(np.bitwise_and((u!=v),np.bitwise_or(u !=0,v!=0)).sum())
            /np.double(np.bitwise_or(u !=0,v!=0)).sum())
    return dist

3. 变量间的相似度度量

3.1 相关系数

记变量 xj 的取值 （x1j,x2j,⋯,xnj） 就可以用两变量的相关系数作为他们的相似性度量:

rjk=∑i=1n(xij−x⎯⎯j)(xik−x⎯⎯k)[∑i=1n(xij−x⎯⎯j)2(xik−x⎯⎯k)2]12(2.3.1)

它的区间为[-1,1]，越接近1，表示正相关，接近-1.表示负相关，等于0，表明两变量独立，互不影响。

在监督学习中，如果特征数量少，可以使用相关系数筛选有用特征，python代码也很简单:

plt.figure(figsize=(12,12))
from seaborn.linearmodels import corrplot,symmatplot

_ = corrplot(df,annot = False)
plt.show()

另外的，我们可以把相关系数写成用随机变量X,Y及其对应的均值 μX,μY 和方差: σX,σY 表示如下：

ρX,Y=corr(X,Y)=E[(X−μX)(Y−μY)]σXσY

,这样用python实现较简单：

def correlation(u,v):
    u = _validate_vector(u)
    v = _validate_vector(v)
    uMean = u.mean()
    vMean = v.mean()
    um = u - uMean
    vm = v - vMean
    dist = np.dot(um,vm)/(norm(um)*norm(vm))

相关距离：

DXY=1−ρXY

3.2 余弦相似度

也可以利用两个变量的夹角余弦作为它们的相似性度量：

rjk=∑i=1nxijxik[∑i=1nx2ij∑i=1nx2ik]12

两者都满足

• |rjk|≤1,对一切的j,k
• rjk=rkj,对一切的j,k

其中 |rjk| 越接近1， xj,xk 就越相似，如果越接近0，相似性就越弱。

用向量表示余弦相似度：

a⃗ ⋅b⃗ =||a⃗ ||||b⃗ ||cosθ

如图所示的角度：

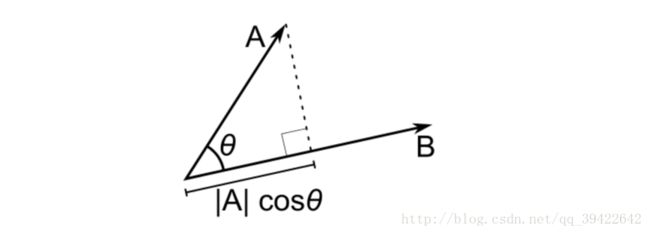
该方法最常用于自然语言处理中，衡量两句话的相似度。
给个应用的例子：

documents = ("the sky is blue",
             "the sun is bright",
             "the sun in the sky is bright",
             "We can see the shinning sun,the bright sun")
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf_vectorizer = TfidfVectorizer()
tfidf_matrix = tfidf_vectorizer.fit_transform(documents)
print tfidf_matrix.shape
(4, 11)

先拿到这四句话的对应的tfidf矩阵，每一行代表一句话，一共有11个terms.然后可以计算一下第一句话与自己及其他三句话的相似度：

from sklearn.metrics.pairwise import cosine_similarity
cosine_similarity(tfidf_matrix[0:1],tfidf_matrix)
array([[ 1.        ,  0.36651513,  0.52305744,  0.13448867]])

余弦距离可以表示为：

Cosine_distance=1.0−cosine_similarity=1.0−a⃗ ⋅b⃗ ||a⃗ ||⋅||b⃗ ||

def cosineDistance(u,v):
    u = _validate_vector(u)
    v = _validate_vector(v)
    dist = 1.0 - np.dot(u,v)/(norm(u)*norm(v))
    return dist
u = [1,2,4,5]
v = [1,2,3,5]
dis = cosineDistance(u,v)
print dis
0.00839645423524

夹角余弦的取值为[-1,1],夹角余弦越大，表示两个向量的夹角越小，夹角余弦越小，表示两个向量的夹角越大，相似性也越低。当夹角余弦为1时，两个向量重合，为-1时，两个向量方向相反。

4.两个概率分布间的相似度度量

4.1 KL散度（Kullback-Leibler divergence）

KL散度在生成式对抗网络GAN中被用来衡量生成分布与真实数据分布之间的相似性。但其本质依然是极大似然估计，因为它能从极大似然估计中推导出来。

而在信息论中，它又被成为相对熵，我们使用香农熵来对整个概率分布中的不确定性进行量化：

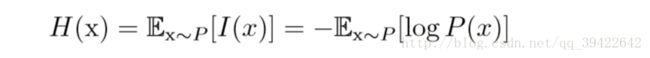
假设对于同一个随机变量x有两个不同的概率分布 P(x),Q(x) ,使用KL散度（相对熵）来衡量他们的相似性如下：

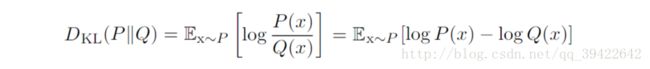
如果他们在离散型变量下为相同的分布，在连续型变量的情况下为几乎处处相同的分布，则他们的KL散度为0，且KL散度为非负。但有一点需要注意的是，KL散度和先前距离不太一样，因为它是不可逆，即：

DKL(P||Q)≠DKL(Q||P)

但既然我把距离抽象成两个东西的相互作用，所以就把这个也写进来了。

E表示期望，因为离散型和连续型的随机变量的期望计算方法不一样，对于离散型随机变量的KL散度计算公式如下：

DKL(P||Q)=∑ip(i) logp(i)q(i)

对于连续型随机变量的KL散度可以写成为：

DKL(P||Q)=∫+∞−∞p(x) logp(x)q(x)

python实现如下：

def discreteKL(pk,qk):
    pk = np.asarray(pk)
    pk = 1.0*pk/np.sum(pk,axis = 0)
    qk = np.asarray(qk)
    qk = 1.0*qk/np.sum(qk,axis = 0)
    if len(pk) != len(qk):
        raise ValueError("pk and qk must have the same length")
    KL = np.sum(np.where(qk != 0, pk*np.log(pk/qk), 0))
    return KL
import numpy as np
import scipy.stats

# 随机生成两个离散型分布
x = [np.random.randint(1, 11) for i in range(10)]
print x
y = [np.random.randint(1, 11) for i in range(10)]
print y 
KL = discreteKL(x,y)
print KL

输出：

[4, 5, 7, 3, 9, 7, 2, 5, 6, 8]
[10, 4, 7, 2, 9, 1, 9, 10, 6, 5]
0.288755527342

调用scipy计算如下

KL = scipy.stats.entropy(x,y)
print KL
0.128572817563

4.2 jensen-shannon距离

JS距离是KL散度的对称，平滑版本。定义如下： M=12(P+Q) ,有：

JSD(P||Q)=12DKL(P||M)+12DKL(Q||M)

4.3 巴氏距离

巴氏距离也是一种衡量分布的相似性度量。

5.对信息的相似度度量

此外还有信息熵，信息增益，我均把他们当成距离，因为我把距离抽象成两个东西的相互关系了，如此更能理解他们之间的内涵。这部分待写。

6.类，群或社区间的相似性度量

这部分包含的内容是两个类间的相似性度量，或者是社区发现算法中的模块度，也是两个对象之间的相似度度量。

7.我眼中的距离到底有多美

这几个部分先欠着，待我对这几个部分有了更深的认识之后再写。

参考
让你看懂聚类分析
Machine Learning :: Cosine Similarity for Vector Space Models (Part III)
scipy/scipy/spatial/distance.py
从K近邻算法、距离度量谈到KD树、SIFT+BBF算法
BAT机器学习面试1000题系列
统计学习方法BR-附录：距离、相似度和熵的度量方法总结【有补充材料】
机器学习相关——协同过滤
Jaccard index
Jensen–Shannon divergence