基础积累 | 必备教程，一文全面理解Pytorch（附代码实例）

点击上方“AI算法修炼营”，选择加星标或“置顶”

标题以下，全是干货

来自 | 知乎   作者 | 瑾er

链接 | https://zhuanlan.zhihu.com/p/111144134

本文仅作学术分享，如有侵权，请联系删除

一、介绍

PyTorch是增长最快的深度学习框架。PyTorch也非常具有Python风格，注重简洁和实用。

此外，也有一些使用者说，使用PyTorch甚至可以改善健康。

二、动机

网上有许多PyTorch教程，它的文档非常完整和广泛。那么，为什么要继续阅读这个循序渐进的教程呢?这份教程以一系列常见的例子为主从基本原理开始讲解。从而使大家对PyTorch的理解更加直观。本文除了这些之外，还将提供一些避免常见陷阱和错误的建议。这份教程内容比较多，因此，为了便于查阅，建立目录如下：

三、目录

• 一个简单的回归问题

• 梯度下降法

• Numpy中的线性回归

• PyTorch

• Autograd

• 动态计算图

• 优化器

• 损失

• 模型

• 数据集

• DataLoader

• 评价

  

 四、一个简单的回归问题

大多数教程都是从一些漂亮的图像分类问题开始，以说明如何使用PyTorch。但是这容易让人偏离原来的目标即：PyTorch是如何工作的?

因此本教程从一个简单的回归问题开始。线性回归模型可表示成如下形式：

很多人认为回归模型就是线性回归，但是不是这样的，回归代表你的模型结果是一个或多个连续值。

   

数据生成

让我们开始生成一些合成数据:我们从特征x的100个点的向量开始，然后使用a = 1, b = 2和一些高斯噪声创建我们的标签。

接下来，让我们将合成数据分解为训练集和验证集，打乱索引数组并使用前80个打乱的点进行训练。

# Data Generation
np.random.seed(42)
x = np.random.rand(100, 1)
y = 1 + 2 * x + .1 * np.random.randn(100, 1)
# Shuffles the indices
idx = np.arange(100)
np.random.shuffle(idx)
# Uses first 80 random indices for train
train_idx = idx[:80]
# Uses the remaining indices for validation
val_idx = idx[80:]
# Generates train and validation sets
x_train, y_train = x[train_idx], y[train_idx]
x_val, y_val = x[val_idx], y[val_idx

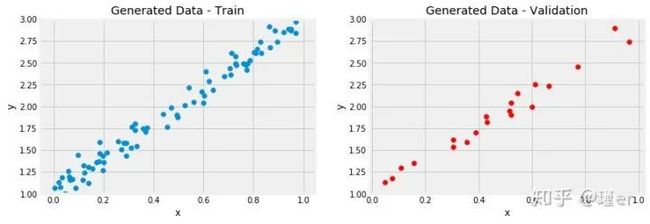
我们知道a = 1 b = 2，但是现在让我们看看如何使用梯度下降和训练集中的80个点来接近真实值的。

   

梯度下降法

关于梯度下降的内部运行机制，前面有篇文章来专门说明。这里只简单介绍梯度下降的四个基本步骤。

步骤1:计算损失

对于回归问题，损失由均方误差(MSE)给出，即标签(y)和预测(a + bx)之间所有平方误差的平均值。

值得一提的是，如果我们使用训练集(N)中的所有点来计算损失，我们是在执行 批量梯度下降。如果我们每次都用一个点，那就是 随机梯度下降法。在1和n之间的任何其他(n)都是 小批量梯度下降的特征。

步骤2:计算梯度

梯度是偏导数，为什么偏导数?因为它是用一个参数(w.r.t)来计算的。我们有两个参数，a和b，所以我们必须计算两个偏导。导数告诉你，当你稍微改变某个量时，这个量的变化量是多少。在我们的例子中，当我们改变两个参数中的一个时，我们的MSE损失变化了多少?

步骤3:更新参数

在最后一步，我们使用梯度来更新参数。因为我们试图最小化我们的损失，所以我们反转了更新的梯度符号。

还需要考虑另一个参数:学习率，用希腊字母eta表示(看起来像字母n)，这是我们需要对梯度进行参数更新的乘法因子，在程序里通常简化为lr.

关于如何选择合适的学习率，这是一个需要大量实践的内容，学习率不能太大，也不能太小。

第四步:重复。

现在，我们使用更新的参数返回步骤1并重新启动流程。

对于批量梯度下降，这是微不足道的，因为它使用所有的点来计算损失-一个轮次等于一个更新。对于随机梯度下降，一个epoch意味着N次更新，而对于小批量(大小为N)，一个epoch有N/n次更新。

简单地说，对于许多时代来说，反复地重复这个过程就是训练一个模型。

   

五、Numpy中的线性回归

接下来就是使用Numpy用梯度下降来实验线性回归模型的时候了。还没有到PyTorch,使用Numpy的原因有两点：

• 介绍任务的结松

• 展示主要的难点，以便能够充分理解使用PyTorch的方便之处。

对于一个模型的训练，有4个初始化步骤:

• 参数/权重的随机初始化(我们只有两个，a和b)——第3行和第4行;

• 超参数的初始化(在我们的例子中，只有学习速率和epoch的数量)——第9行和第11行; 确保始终初始化您的随机种子，以确保您的结果的再现性。和往常一样，随机的种子是42，是所有随机种子中最不随机的:-)

每个epoch有四个训练步骤:

• 计算模型的预测——这是正向传递——第15行;

• 计算损失，使用预测和标签，以及当前任务的适当损失函数——第18行和第20行;

• 计算每个参数的梯度——第23行和第24行;

• 更新参数——第27行和第28行; 请记住，如果您不使用批量梯度下降(我们的示例使用)，则必须编写一个内部循环来为每个点(随机)或n个点(迷你批量)执行四个训练步骤。稍后我们将看到一个小型批处理示例。

# Initializes parameters "a" and "b" randomly
np.random.seed(42)
a = np.random.randn(1)
b = np.random.randn(1)


print(a, b)


# Sets learning rate
lr = 1e-1
# Defines number of epochs
n_epochs = 1000


for epoch in range(n_epochs):
    # Computes our model's predicted output
    yhat = a + b * x_train


    # How wrong is our model? That's the error!
    error = (y_train - yhat)
    # It is a regression, so it computes mean squared error (MSE)
    loss = (error ** 2).mean()


    # Computes gradients for both "a" and "b" parameters
    a_grad = -2 * error.mean()
    b_grad = -2 * (x_train * error).mean()


    # Updates parameters using gradients and the learning rate
    a = a - lr * a_grad
    b = b - lr * b_grad


print(a, b)


# Sanity Check: do we get the same results as our gradient descent?
from sklearn.linear_model import LinearRegression
linr = LinearRegression()
linr.fit(x_train, y_train)
print(linr.intercept_, linr.coef_[0])

结果是：

# a and b after initialization
[0.49671415] [-0.1382643]
# a and b after our gradient descent
[1.02354094] [1.96896411]
# intercept and coef from Scikit-Learn
[1.02354075] [1.96896447]

以上是Numpy的做法，接下来我们看一看PyTorch的做法。

   

六、PyTorch

首先，我们需要介绍一些基本概念。

在深度学习中，张量无处不在。嗯，谷歌的框架被称为TensorFlow是有原因的，那到底什么是张量?

   

张量

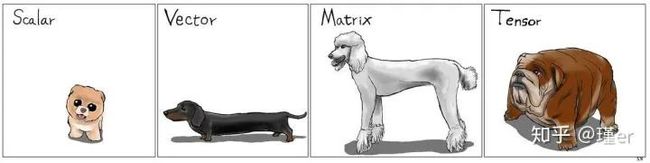
张量（tensor）是多维数组，目的是把向量、矩阵推向更高的维度。

一个标量(一个数字)有0维，一个向量有1维，一个矩阵有2维，一个张量有3维或更多。但是，为了简单起见，我们通常也称向量和矩阵为张量。

   

加载数据，设备和CUDA

你可能会问:“我们如何从Numpy的数组过渡到PyTorch的张量?”这就是from_numpy的作用。它返回一个CPU张量。

如何要使用GPU,那么它会把张量发送到GPU上面。“如果我想让我的代码回退到CPU，如果没有可用的GPU ?”你可以使用cuda.is_available()来找出你是否有一个GPU供你使用，并相应地设置你的设备。当然还可以使用float()轻松地将其转换为较低精度(32位浮点数)。

import torch
import torch.optim as optim
import torch.nn as nn
from torchviz import make_dot


device = 'cuda' if torch.cuda.is_available() else 'cpu'


# Our data was in Numpy arrays, but we need to transform them into PyTorch's Tensors
# and then we send them to the chosen device
x_train_tensor = torch.from_numpy(x_train).float().to(device)
y_train_tensor = torch.from_numpy(y_train).float().to(device)


# Here we can see the difference - notice that .type() is more useful
# since it also tells us WHERE the tensor is (device)
print(type(x_train), type(x_train_tensor), x_train_tensor.type())

如果比较这两个变量的类型，就会得到预期的结果第一种代码用的是numpy.ndarray,第三种代码用的是torch.Tensor.

使用PyTorch的type()，它会显示它的位置。

我们也可以反过来，使用Numpy()将张量转换回Numpy数组。它应该像x_train_tensor.numpy()一样简单，但是…

TypeError: can't convert CUDA tensor to numpy. Use Tensor.cpu() to copy the tensor to host memory first.

非常遗憾，Numpy不能处理GPU张量。

   

创建参数

如何区分用于数据的张量（就像我们刚刚创建的那些）和用作(可训练的)参数/权重的张量?

后一个张量需要计算它的梯度，所以我们可以更新它们的值(即参数的值)。这就是requires_grad=True参数的作用。它告诉PyTorch我们想让它为我们计算梯度。

你可能想为一个参数创建一个简单的张量，然后把它发送到所选择的设备上，就像我们处理数据一样，对吧? 但其实没那么快……

# FIRST
# Initializes parameters "a" and "b" randomly, ALMOST as we did in Numpy
# since we want to apply gradient descent on these parameters, we need
# to set REQUIRES_GRAD = TRUE
a = torch.randn(1, requires_grad=True, dtype=torch.float)
b = torch.randn(1, requires_grad=True, dtype=torch.float)
print(a, b)


# SECOND
# But what if we want to run it on a GPU? We could just send them to device, right?
a = torch.randn(1, requires_grad=True, dtype=torch.float).to(device)
b = torch.randn(1, requires_grad=True, dtype=torch.float).to(device)
print(a, b)
# Sorry, but NO! The to(device) "shadows" the gradient...


# THIRD
# We can either create regular tensors and send them to the device (as we did with our data)
a = torch.randn(1, dtype=torch.float).to(device)
b = torch.randn(1, dtype=torch.float).to(device)
# and THEN set them as requiring gradients...
a.requires_grad_()
b.requires_grad_()
print(a, b)

第一个代码块为我们的参数、梯度和所有东西创建了两个很好的张量。但它们是CPU张量。

# FIRST
tensor([-0.5531], requires_grad=True)
tensor([-0.7314], requires_grad=True)

在第二段代码中，我们尝试了将它们发送到我们的GPU的简单方法。我们成功地将它们发送到另一个设备上，但是我们不知怎么地“丢失”了梯度……

# SECOND
tensor([0.5158], device='cuda:0', grad_fn=) tensor([0.0246], device='cuda:0', grad_fn=)

在第三块中，我们首先将张量发送到设备，然后使用requires_grad_()方法将其requires_grad设置为True。

在PyTorch中，每个以下划线(_)结尾的方法都会进行适当的更改，这意味着它们将修改底层变量。

尽管最后一种方法工作得很好，但最好在设备创建时将张量分配给它们。

# We can specify the device at the moment of creation - RECOMMENDED!
torch.manual_seed(42)
a = torch.randn(1, requires_grad=True, dtype=torch.float, device=device)
b = torch.randn(1, requires_grad=True, dtype=torch.float, device=device)
print(a, b)
tensor([0.6226], device='cuda:0', requires_grad=True) tensor([1.4505], device='cuda:0', requires_grad=True)

容易多了,对吧? 现在我们知道了如何创建需要梯度的张量，让我们看看PyTorch如何处理它们

Autograd

Autograd是PyTorch的自动微分包。

那么，我们如何让PyTorch完成它的任务并计算所有的梯度呢?这就是backward()的好处。

还记得计算梯度的起点吗?这是loss。因此，我们需要从相应的Python变量中调用backward()方法，比如，loss. backwards()。

那么梯度的实际值呢?我们可以通过观察张量的grad属性来考察它们。

如果你查看该方法的文档，就会清楚地看到渐变是累积的。因此，每次我们使用梯度来更新参数时，我们都需要在之后将梯度归零。这就是zero_()的好处。

因此，让我们抛弃手工计算梯度的方法，同时使用backward()和zero_()方法。就这些吗? 嗯，差不多…但是，总是有一个陷阱，这一次它与参数的更新有关…

lr = 1e-1
n_epochs = 1000


torch.manual_seed(42)
a = torch.randn(1, requires_grad=True, dtype=torch.float, device=device)
b = torch.randn(1, requires_grad=True, dtype=torch.float, device=device)


for epoch in range(n_epochs):
    yhat = a + b * x_train_tensor
    error = y_train_tensor - yhat
    loss = (error ** 2).mean()


    # No more manual computation of gradients!
    # a_grad = -2 * error.mean()
    # b_grad = -2 * (x_tensor * error).mean()


    # We just tell PyTorch to work its way BACKWARDS from the specified loss!
    loss.backward()
    # Let's check the computed gradients...
    print(a.grad)
    print(b.grad)


    # What about UPDATING the parameters? Not so fast...


    # FIRST ATTEMPT
    # AttributeError: 'NoneType' object has no attribute 'zero_'
    # a = a - lr * a.grad
    # b = b - lr * b.grad
    # print(a)


    # SECOND ATTEMPT
    # RuntimeError: a leaf Variable that requires grad has been used in an in-place operation.
    # a -= lr * a.grad
    # b -= lr * b.grad


    # THIRD ATTEMPT
    # We need to use NO_GRAD to keep the update out of the gradient computation
    # Why is that? It boils down to the DYNAMIC GRAPH that PyTorch uses...
    with torch.no_grad():
        a -= lr * a.grad
        b -= lr * b.grad


    # PyTorch is "clingy" to its computed gradients, we need to tell it to let it go...
    a.grad.zero_()
    b.grad.zero_()


print(a, b)

在第一次尝试中,如果我们使用相同的更新结构如Numpy代码,我们会得到下面的奇怪的错误,我们再次“失去”梯度而重新分配参数更新结果。因此，grad属性为None，它会引发错误…

# FIRST ATTEMPT
tensor([0.7518], device='cuda:0', grad_fn=)
AttributeError: 'NoneType' object has no attribute 'zero_'

然后，我们稍微更改一下，在第二次尝试中使用熟悉的就地Python赋值。而且，PyTorch再一次抱怨它并提出一个错误。

# SECOND ATTEMPT
RuntimeError: a leaf Variable that requires grad has been used in an in-place operation.

为什么? !事实证明，这是一个“好事过头”的例子。罪魁祸首是PyTorch的能力，它能够从每一个涉及到任何梯度计算张量或其依赖项的Python操作中构建一个动态计算图。在下一节中，我们将深入讨论动态计算图的内部工作方式。

那么，我们如何告诉PyTorch“后退”并让我们更新参数，而不打乱它的动态计算图呢? 这就是torch.no_grad()。no_grad()的好处。它允许我们对张量执行常规的Python操作，与PyTorch的计算图无关。

最后，我们成功地运行了我们的模型并获得了结果参数。当然，它们与我们在纯numpy实现中得到的那些差不多。

# THIRD ATTEMPT
tensor([1.0235], device='cuda:0', requires_grad=True)
tensor([1.9690], device='cuda:0', requires_grad=True)

   

动态计算图

目前神经网络框架分为静态图框架和动态图框架，PyTorch 和 TensorFlow、Caffe 等框架最大的区别就是他们拥有不同的计算图表现形式。 TensorFlow 使用静态图，这意味着我们先定义计算图，然后不断使用它，而在 PyTorch 中，每次都会重新构建一个新的计算图。

对于使用者来说，两种形式的计算图有着非常大的区别，同时静态图和动态图都有他们各自的优点，比如动态图比较方便debug，使用者能够用任何他们喜欢的方式进行debug，同时非常直观，而静态图是通过先定义后运行的方式，之后再次运行的时候就不再需要重新构建计算图，所以速度会比动态图更快。

PyTorchViz包及其make_dot(变量)方法允许我们轻松地可视化与给定Python变量关联的图。

torch.manual_seed(42)
a = torch.randn(1, requires_grad=True, dtype=torch.float, device=device)
b = torch.randn(1, requires_grad=True, dtype=torch.float, device=device)


yhat = a + b * x_train_tensor
error = y_train_tensor - yhat
loss = (error ** 2).mean()

如果我们调用make_dot(yhat)，我们将得到下面图中最左边的图形:

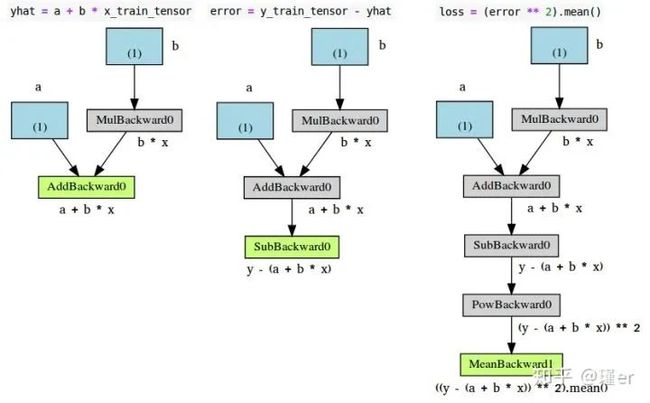
让我们仔细看看它的组成部分:

• 蓝方框:这些对应于我们用作参数的张量，也就是我们要求PyTorch计算梯度的张量;

• 灰箱:包含梯度计算张量或其相依关系的Python操作;

• 绿色方框:与灰色方框相同，只是它是渐变计算的起点(假设使用reverse()方法从用于可视化图形的变量中调用)——它们是从图形中的自底向上计算的。

如果我们为error(中间)和loss(右边)变量绘制图形，那么它们与第一个变量之间的惟一区别就是中间步骤的数量(灰色框)。

现在，仔细看看最左边的绿色方框:有两个箭头指向它，因为它将两个变量a和b*x相加。

然后，看一下同一图形的灰框:它执行的是乘法，即b*x。但是只有一个箭头指向它!箭头来自于对应于参数b的蓝色方框。

为什么我们没有数据x的方框呢?答案是:我们不为它计算梯度!因此，即使计算图所执行的操作涉及到更多的张量，也只显示了梯度计算张量及其依赖关系。

如果我们将参数a的requires_grad设为False，计算图形会发生什么变化?

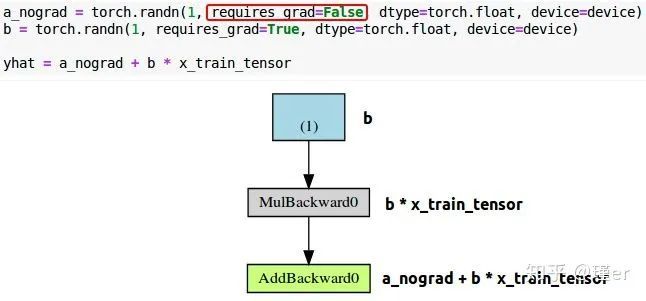
不出所料，与参数a对应的蓝色框是no more!很简单:没有梯度，没有图形。

动态计算图最好的地方在于你可以让它变得像你想要的那样复杂。甚至可以使用控制流语句(例如，if语句)来控制梯度流(显然!)

下面的图显示了一个示例。

   

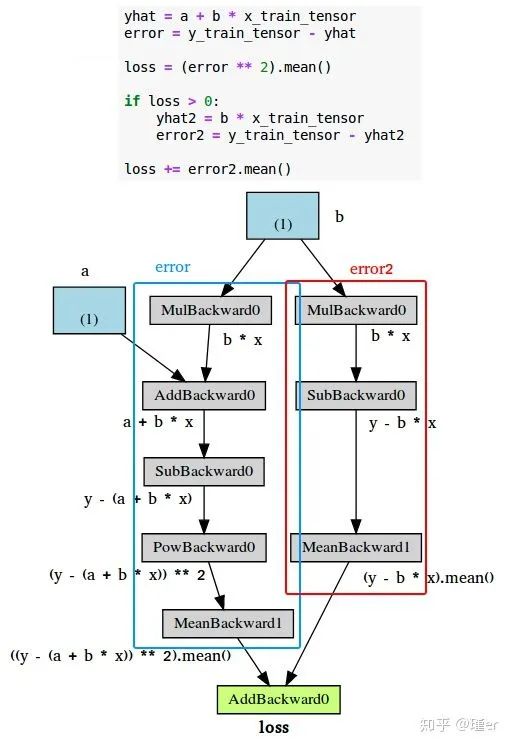
优化器

到目前为止，我们一直在使用计算出的梯度手动更新参数。这对于两个参数来说可能很好，但是如果我们有很多参数呢?我们使用PyTorch的一个优化器，比如SGD或Adam。

优化器获取我们想要更新的参数、我们想要使用的学习率(可能还有许多其他超参数!)并通过其step()方法执行更新。

此外，我们也不需要一个接一个地将梯度归零。我们只需调用优化器的zero_grad()方法就可以了! 在下面的代码中，我们创建了一个随机梯度下降(SGD)优化器来更新参数a和b。

不要被优化器的名字所欺骗:如果我们一次使用所有的训练数据进行更新——就像我们在代码中所做的那样——优化器执行的是批量梯度下降，而不是它的名字。

torch.manual_seed(42)
a = torch.randn(1, requires_grad=True, dtype=torch.float, device=device)
b = torch.randn(1, requires_grad=True, dtype=torch.float, device=device)
print(a, b)


lr = 1e-1
n_epochs = 1000


# Defines a SGD optimizer to update the parameters
optimizer = optim.SGD([a, b], lr=lr)


for epoch in range(n_epochs):
    yhat = a + b * x_train_tensor
    error = y_train_tensor - yhat
    loss = (error ** 2).mean()


    loss.backward()


    # No more manual update!
    # with torch.no_grad():
    #     a -= lr * a.grad
    #     b -= lr * b.grad
    optimizer.step()


    # No more telling PyTorch to let gradients go!
    # a.grad.zero_()
    # b.grad.zero_()
    optimizer.zero_grad()


print(a, b)

让我们检查一下之前和之后的两个参数，以确保一切正常:

# BEFORE: a, b
tensor([0.6226], device='cuda:0', requires_grad=True) tensor([1.4505], device='cuda:0', requires_grad=True)
# AFTER: a, b
tensor([1.0235], device='cuda:0', requires_grad=True) tensor([1.9690], device='cuda:0', requires_grad=True)

   

损失

PyTorch集成了很多损失函数。在这个例子中我们使用的是MSE损失。

注意 nn.MSELoss实际上为我们创建了一个损失函数——它不是损失函数本身。此外，你还可以指定一个要应用的reduction method，即如何聚合单个点的结果—你可以对它们进行平均(约简= ' mean ')，或者简单地对它们求和(约简= ' sum ')。

然后在第20行使用创建的损失函数，根据我们的预测和标签计算损失。

我们的代码是这样的:

torch.manual_seed(42)
a = torch.randn(1, requires_grad=True, dtype=torch.float, device=device)
b = torch.randn(1, requires_grad=True, dtype=torch.float, device=device)
print(a, b)


lr = 1e-1
n_epochs = 1000


# Defines a MSE loss function
loss_fn = nn.MSELoss(reduction='mean')


optimizer = optim.SGD([a, b], lr=lr)


for epoch in range(n_epochs):
    yhat = a + b * x_train_tensor


    # No more manual loss!
    # error = y_tensor - yhat
    # loss = (error ** 2).mean()
    loss = loss_fn(y_train_tensor, yhat)


    loss.backward()
    optimizer.step()
    optimizer.zero_grad()


print(a, b)

   

模型

在PyTorch中，model由一个常规的Python类表示，该类继承自Module类。

它需要实现的最基本的方法是:

__init__(self)定义了组成模型的两个参数:a和b。

模型可以包含其他模型作为它的属性，所以可以很容易实现嵌套。

forward(self, x):它执行了实际的计算，也就是说，给定输入x，它输出一个预测。

让我们为我们的回归任务构建一个适当的(但简单的)模型。它应该是这样的:

class ManualLinearRegression(nn.Module):
    def __init__(self):
        super().__init__()
        # To make "a" and "b" real parameters of the model, we need to wrap them with nn.Parameter
        self.a = nn.Parameter(torch.randn(1, requires_grad=True, dtype=torch.float))
        self.b = nn.Parameter(torch.randn(1, requires_grad=True, dtype=torch.float))


    def forward(self, x):
        # Computes the outputs / predictions
        return self.a + self.b * x

在_init__方法中，我们定义了两个参数，a和b，使用Parameter()类，告诉PyTorch应该将这些张量视为它们是的属性的模型参数。

我们为什么要关心这个?通过这样做，我们可以使用模型的parameters()方法来检索所有模型参数的迭代器，甚至是那些嵌套模型的参数，我们可以使用它们来提供我们的优化器(而不是自己构建参数列表!) 此外，我们可以使用模型的state_dict()方法获取所有参数的当前值。

重要提示:我们需要将模型发送到数据所在的同一设备。如果我们的数据是由GPU张量构成的，我们的模型也必须“活”在GPU内部。

我们可以使用所有这些方便的方法来改变我们的代码，应该是这样的:

torch.manual_seed(42)


# Now we can create a model and send it at once to the device
model = ManualLinearRegression().to(device)
# We can also inspect its parameters using its state_dict
print(model.state_dict())


lr = 1e-1
n_epochs = 1000


loss_fn = nn.MSELoss(reduction='mean')
optimizer = optim.SGD(model.parameters(), lr=lr)


for epoch in range(n_epochs):
    # What is this?!?
    model.train()


    # No more manual prediction!
    # yhat = a + b * x_tensor
    yhat = model(x_train_tensor)


    loss = loss_fn(y_train_tensor, yhat)
    loss.backward()
    optimizer.step()
    optimizer.zero_grad()


print(model.state_dict())

现在打印出来的语句将是这样的--参数a和参数b的最终值仍然相同，所以一切正常。

OrderedDict([('a', tensor([0.3367], device='cuda:0')), ('b', tensor([0.1288], device='cuda:0'))])
OrderedDict([('a', tensor([1.0235], device='cuda:0')), ('b', tensor([1.9690], device='cuda:0'))])

在PyTorch中，模型有一个 train()方法，有点令人失望的是，它没有执行训练步骤。其唯一目的是将模型设置为训练模式。为什么这很重要?有些模型可能使用Dropout机制，在训练和评估阶段有不同的行为。

   

嵌套模型

在我们的模型中，我们手动创建了两个参数来执行线性回归。让我们使用PyTorch的Linear模型作为我们自己的属性，从而创建一个嵌套模型。

尽管这显然是一个人为设计的示例，因为我们几乎是在包装底层模型，而没有向其添加任何有用的东西，但它很好地说明了这个概念。

在_init__方法中，我们创建了一个包含嵌套线性模型的属性。在forward()方法中，我们调用嵌套模型本身来执行forward传递(注意，我们没有调用self.linear.forward(x))。

class LayerLinearRegression(nn.Module):
    def __init__(self):
        super().__init__()
        # Instead of our custom parameters, we use a Linear layer with single input and single output
        self.linear = nn.Linear(1, 1)


    def forward(self, x):
        # Now it only takes a call to the layer to make predictions
        return self.linear(x)

现在，如果我们调用这个模型的parameters()方法，PyTorch将以递归方式显示其属性的参数。您可以使用类似于[*LayerLinearRegression().parameters()]的方法来获得所有参数的列表。你还可以添加新的线性属性，即使在前向传递中根本不使用它们，它们仍然会在parameters()下列出。

   

顺序模型

我们的模型非常简单……你可能会想:“为什么要为它构建一个类呢?”“

对于使用普通层的简单模型，其中一层的输出按顺序作为下一层的输入，我们可以使用Sequential模型。

在我们的例子中，我们将使用单个参数构建一个序列模型，即我们用来训练线性回归的线性层。模型应该是这样的:

# Alternatively, you can use a Sequential model
model = nn.Sequential(nn.Linear(1, 1)).to(device)

非常简单。

   

训练步骤

到目前为止，我们已经定义了优化器、损失函数和模型。向上滚动一点，快速查看循环中的代码。如果我们使用不同的优化器，或者损失，甚至模型，它会改变吗?如果不是，我们如何使它更通用?

好吧，我想我们可以说所有这些代码行执行一个训练步骤，给定这三个元素(优化器、损失和模型)、特性和标签。

那么，如何编写一个函数来获取这三个元素并返回另一个函数来执行一个训练步骤，将一组特性和标签作为参数并返回相应的损失呢?

然后，我们可以使用这个通用函数来构建一个train_step()函数，以便在训练循环中调用。现在我们的代码应该是这样的……看到训练循环有多小?

def make_train_step(model, loss_fn, optimizer):
    # Builds function that performs a step in the train loop
    def train_step(x, y):
        # Sets model to TRAIN mode
        model.train()
        # Makes predictions
        yhat = model(x)
        # Computes loss
        loss = loss_fn(y, yhat)
        # Computes gradients
        loss.backward()
        # Updates parameters and zeroes gradients
        optimizer.step()
        optimizer.zero_grad()
        # Returns the loss
        return loss.item()


    # Returns the function that will be called inside the train loop
    return train_step


# Creates the train_step function for our model, loss function and optimizer
train_step = make_train_step(model, loss_fn, optimizer)
losses = []


# For each epoch...
for epoch in range(n_epochs):
    # Performs one train step and returns the corresponding loss
    loss = train_step(x_train_tensor, y_train_tensor)
    losses.append(loss)


# Checks model's parameters
print(model.state_dict())

暂时把注意力放在我们的数据上……到目前为止，我们只是简单地使用了由Numpy数组转换而来的PyTorch张量。但我们可以做得更好，我们可以建立一个Pytorch张量数据。

   

数据集

在PyTorch中，dataset由一个常规的Python类表示，该类继承自dataset类。你可以将它的睦作一种Python元组列表，每个元组对应于一个数据点（特性，标签）。

它需要实现的最基本的方法是： __init__(self)：它采取任何参数需要建立一个元组列表-它可能是一个名称的CSV文件，将加载和处理;它可以是两个张量，一个代表特征，另一个代表标签;或者其他的，取决于手头的任务。

不需要在构造函数方法中加载整个数据集。如果数据集很大(例如，成千上万的图像文件)，立即加载它将是内存效率不高的。建议按需加载它们(无论何时调用了 _get_item__)。

_get_item__(self, index):它允许数据集被索引，因此它可以像列表一样工作(dataset)——它必须返回与请求的数据点对应的元组(特性，标签)。我们可以返回预先加载的数据集或张量的相应切片，或者，如前所述，按需加载它们(如本例中所示)。

__len__(self):它应该简单地返回整个数据集的大小，这样，无论什么时候采样它，它的索引都被限制在实际大小。

让我们构建一个简单的自定义数据集，它接受两个张量作为参数:一个用于特性，一个用于标签。对于任何给定的索引，我们的数据集类将返回每个张量的对应切片。它应该是这样的:

from torch.utils.data import Dataset, TensorDataset


class CustomDataset(Dataset):
    def __init__(self, x_tensor, y_tensor):
        self.x = x_tensor
        self.y = y_tensor


    def __getitem__(self, index):
        return (self.x[index], self.y[index])


    def __len__(self):
        return len(self.x)


# Wait, is this a CPU tensor now? Why? Where is .to(device)?
x_train_tensor = torch.from_numpy(x_train).float()
y_train_tensor = torch.from_numpy(y_train).float()


train_data = CustomDataset(x_train_tensor, y_train_tensor)
print(train_data[0])


train_data = TensorDataset(x_train_tensor, y_train_tensor)
print(train_data[0])

再一次，你可能会想“为什么要在一个类中经历这么多麻烦来包装几个张量呢?”如果一个数据集只是两个张量，那么我们可以使用PyTorch的TensorDataset类，它将完成我们在上面的自定义数据集中所做的大部分工作。

你注意到我们用Numpy数组构建了我们的训练张量，但是我们没有将它们发送到设备上吗?所以，它们现在是CPU张量!为什么?

我们不希望我们的全部训练数据都被加载到GPU张量中，就像我们到目前为止的例子中所做的那样，因为它占用了我们宝贵的显卡RAM中的空间。

构建数据集的作用是因为我们想用。

   

DataLoader

到目前为止，我们在每个训练步骤都使用了全部的训练数据。一直以来都是批量梯度下降。

这对于我们的小得可笑的数据集来说当然很好，但是对于一些大的数据集，我们必须使用小批量梯度下降。因此，我们需要小批量。因此，我们需要相应地分割数据集。

因此我们使用PyTorch的DataLoader类来完成这项工作。我们告诉它使用哪个数据集(我们在前一节中刚刚构建的数据集)、所需的mini-batch处理大小，以及我们是否希望对其进行洗牌。

我们的加载器将表现得像一个迭代器，因此我们可以循环它并每次获取不同的mini-batch批处理。

from torch.utils.data import DataLoader


train_loader = DataLoader(dataset=train_data, batch_size=16, shuffle=True)

要检索一个mini-batch批处理示例，只需运行下面的命令—它将返回一个包含两个张量的列表，一个用于特征，另一个用于标签。

next(iter(train_loader))

重新看一下训练循环，看一下这些是如何对循环做出改变的，我们来看看。

losses = []
train_step = make_train_step(model, loss_fn, optimizer)


for epoch in range(n_epochs):
    for x_batch, y_batch in train_loader:
        # the dataset "lives" in the CPU, so do our mini-batches
        # therefore, we need to send those mini-batches to the
        # device where the model "lives"
        x_batch = x_batch.to(device)
        y_batch = y_batch.to(device)


        loss = train_step(x_batch, y_batch)
        losses.append(loss)


print(model.state_dict())

现在有两件事不同了:我们不仅有一个内部循环来从DataLoader加载每个mini-batch批处理，而且更重要的是，我们现在只向设备发送一个mini-batch批处理。

对于更大的数据集，使用Dataset的_get_item__将一个样本一个样本地加载(到一个CPU张量中)，然后将属于同一小批处理的所有样本一次性发送到你的GPU(设备)是为了充分利用你的显卡RAM的方法。

此外，如果有许多gpu来训练您的模型，那么最好保持数据集“不可知”，并在训练期间将这些批分配给不同的gpu。

到目前为止，我们只关注训练数据。我们为它建立了一个数据集和一个数据加载器。我们可以对验证数据做同样的事情，使用我们在这篇文章开始时执行的分割…或者我们可以使用random_split。

   

随机分割

PyTorch的random_split()方法是执行训练验证分离的一种简单而熟悉的方法。请记住，在我们的示例中，我们需要将它应用到整个数据集(而不是我们在前两节中构建的培训数据集)。

然后，对于每个数据子集，我们构建一个相应的DataLoader，因此我们的代码如下:

from torch.utils.data.dataset import random_split


x_tensor = torch.from_numpy(x).float()
y_tensor = torch.from_numpy(y).float()


dataset = TensorDataset(x_tensor, y_tensor)


train_dataset, val_dataset = random_split(dataset, [80, 20])


train_loader = DataLoader(dataset=train_dataset, batch_size=16)
val_loader = DataLoader(dataset=val_dataset, batch_size=20)

现在，我们的验证集有了一个数据加载器。

   

六、评价

我们需要更改训练循环，以包括对模型的评估，即计算验证损失。第一步是包含另一个内部循环来处理来自验证加载程序的mini-batch，将它们发送到与我们的模型相同的设备。接下来，我们使用模型进行预测，并计算相应的损失。

差不多了，但有两件小事需要考虑:

torch_grad():虽然在我们的简单模型中没有什么不同，但是使用这个上下文管理器来包装验证内部循环是一个很好的实践，这样可以禁用您可能无意中触发的任何梯度计算——梯度属于训练，而不是验证步骤;

eval():它所做的唯一一件事就是将模型设置为评估模式(就像它的train()对手所做的那样)，这样模型就可以根据某些操作(比如Dropout)调整自己的行为。

现在，我们的训练是这种样子的：

losses = []
val_losses = []
train_step = make_train_step(model, loss_fn, optimizer)


for epoch in range(n_epochs):
    for x_batch, y_batch in train_loader:
        x_batch = x_batch.to(device)
        y_batch = y_batch.to(device)


        loss = train_step(x_batch, y_batch)
        losses.append(loss)


    with torch.no_grad():
        for x_val, y_val in val_loader:
            x_val = x_val.to(device)
            y_val = y_val.to(device)


            model.eval()


            yhat = model(x_val)
            val_loss = loss_fn(y_val, yhat)
            val_losses.append(val_loss.item())


print(model.state_dict())

   

七、总结

希望在完成本文中所有的代码后，你能够更好地理解PyTorch官方教程，并更轻松地学习它。

参考链接:

Understanding PyTorch with an example: a step-by-step tutorial