数学建模之倚天剑与屠龙刀
本文来自作者 Waves 在 GitChat 上分享 「数学建模之倚天剑与屠龙刀」
编辑 | 哈比
本 Chat 基于竞赛基础整理,非技术深度博文。
1. 认识数学建模
数学建模:从 1985 年美国的 MCM(Mathematical Contest in Modeling)一直发展至今。
亚里士多德说,“智慧不仅仅存在于知识之中,而且还存在于应用知识的能力中”。数学建模就是对数学知识最好的应用。
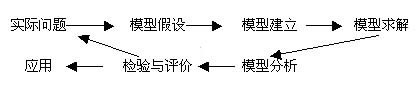
通过数学建模,你会发现,生活中很多有意思的事情都可以靠它来解决,其结构如下:
2. 应该怎么查找数据?
数据来源查找主要有三个模式:
题目来源数据;
题目来源数据 + 中外文期刊数据库(含统计年鉴);
题目来源数据 + 中外文期刊数据库(含统计年鉴)+ 爬虫数据。
附:中外文数据库
中文:CNKI、VIP、万方
外文:EBSCO、Elserive、ProQuest、Springerlink、EI、ISI Web of Knowledge
统计年鉴:National data 国家数据、中国国家统计局年鉴。
开放实验数据源:C Irvine Machine Learning Repository:https://goo.gl/ZzahzM。
UCI 指的是加州大学欧文分校。UCI 机器学习库主要是收集的机器学习领域的一些相关数据集和数据生成器,可以用来做一些基本的实验。
下图即可看见非常经典的 iris 数据。
3. 数据预处理和数据异常处理之间有什么区别?
数据预处理包含数据异常处理。数据预处理常常会包含:数据异常处理,数据空缺处理,无效数据处理,数据分类处理等。
常常使用的办法会有:剔除数据点,拟合模拟数据,对数据进行统计分类等。
4. 软件很多、算法很多,到底应该如何选择?
用一个故事说明:某男到医院就诊,医生亲切地问了一些该男的症状,最后得出结论:“我怀孕了……”
很荒谬吧?其实医生也需要一个好的模型诊断器,根据病人的一系列症状,从而得出病人患的是什么病。
4.1 软件方面
对于数学建模用到最多的软件有:Matlab、Mathmatic、 Lingo/LinDo、SAS、SPSS。
其中前两个主要为计算软件(也可做优化),中间的那个为优化软件,最后两个为统计分析软件。由于时间太紧了,Java、C++ 之类则在竞赛中很少用。
个人推荐:R 和 Python,从定位角度看,R 致力于提供更好的,对用户友好的数据分析、统计分析和绘图模型;而 Python 则强调生产效率和代码的可读性。
4.2 算法方面
数学建模常常可以划分成不同的模型需求:比如说优化模型、微分方程模型、统计模型、概率模型、图论模型、决策模型。
数学建模算法中常用的涉及:类比法、二分法、差分法、变分法、图论法、层次分析法、数据拟合法、回归分析法、数学规划(线性规划,非线性规划,整数规划,动态规划,目标规划)、机理分析、排队方法、对策方法、决策方法、模糊评判方法、时间序列方法、灰色理论方法、现代优化算法(禁忌搜索算法,模拟退火算法,遗传算法,神经网络)等。
其中层次分析法(AHP)是为数不多的主观方法,在评价模型中经常被引用,尤其当没有模型选择时,可以考虑使用!
在优化方法中在,决策变量、目标函数(尽量简单、光滑)、约束条件、求解方法是四个关键因素。
其中包括无约束规则、线性规则(用 Lingo 实现实现比较方便)非线性规则、0-1 规划,多目标规划(有目标加权、效用函数)动态规划、整数规划,适合软件(Matlab、 Lingo、R 和 python)。
回归分析:对具有相关关系的现象,根据其关系形态,选择一个合适的数学模型,用来近似地表示变量间的平均变化关系的一种统计方法 (一元线性回归、多元线性回归、非线性回归)。
回归分析在一组数据的基础上研究这样几个问题:建立因变量与自变量之间的回归模型(经验公式);对回归模型的可信度进行检验;判断每个自变量对因变量的影响是否显著;判断回归模型是否适合这组数据;利用回归模型对进行预报或控制。
相对应的有线性回归、多元二项式回归、非线性回归(比较方便的软件 Matlab、Mathmatic、Lingo/LinDo、SAS、SPSS、R 和 python)。
逐步回归分析:从一个自变量开始,视自变量作用的显著程度,从大到地依次逐个引入回归方程。
当引入的自变量由于后面变量的引入而变得不显著时,要将其剔除掉;引入一个自变量或从回归方程中剔除一个自变量,为逐步回归的一步。
对于每一步都要进行值检验,以确保每次引入新的显著性变量前回归方程中只包含对作用显著的变量。
这个过程反复进行,直至既无不显著的变量从回归方程中剔除,又无显著变量可引入回归方程时为止(软件方面 SAS、matlab、R 和 python)。
时间序列是按时间顺序排列的、随时间变化且相互关联的数据序列—通过对预测目标自身时间序列的处理,来研究其变化趋势(长期趋势变动、季节变动、循环变动、不规则变动)。
时间序列建模的基本步骤
数据的预处理:数据的剔取及提取趋势项。
取 n=1,拟合 ARMA(2n,2n-1)(即 ARMA(2,1))模型。
n=n+1,拟合 ARMA(2n,2n-1) 模型。
用 F 准则检验模型的适用性。若检验显著,则转入第 2 步。若检验不显著,转入第 5 步。
检查远端时刻的系数值的值是否很小,其置信区间是否包含零。若不是,则适用的模型就是 ARMA(2n,2n-1) 。若很小,且其置信区间包含零,则拟合 ARMA(2n-1,2n-2) 。
利用 F 准则检验模型 ARMA(2n,2n-1) 和 ARMA(2n-1,2n-2) ,若 F 值不显著,转入第 7 步;若 F 值显著,转入第 8 步。
舍弃小的 MA 参数,拟合 m<2n-2 的模型 ARMA(2n-1,m) ,并用 F 准则进行检验。重复这一过程,直到得出具有最小参数的适用模型为止。
舍弃小的 MA 参数,拟合 m<2n-1 的模型 ARMA(2n,m) ,并用 F 准则进行检验。重复这一过程,直到得出具有最小参数的适用模型为止。
聚类方法聚类方法对比:https://goo.gl/xH7C2k。
图论方法:
最短路问题:两个指定顶点之间的最短路径—给出了一个连接若干个城镇的铁路网络,在这个网络的两个指定城镇间,找一条最短铁路线 (Dijkstra 算法 )每对顶点之间的最短路径 (Dijkstra 算法、Floyd 算法 )。
最小生成树问题:连线问题—欲修筑连接多个城市的铁路设计一个线路图,使总造价最低(prim 算法、Kruskal 算法 )。
图的匹配问题:人员分派问题:n 个工作人员去做件 n 份工作,每人适合做其中一件或几件,问能否每人都有一份适合的工作?如果不能,最多几人可以有适合的工作?(匈牙利算法)。
遍历性问题:中国邮递员问题—邮递员发送邮件时,要从邮局出发,经过他投递范围内的每条街道至少一次,然后返回邮局,但邮递员希望选择一条行程最短的路线。
最小费用问题:在运输问题中,人们总是希望在完成运输任务的同时,寻求一个使总的运输费用最小的运输方案。
5. 建立了模型,某些相关参数偏差很厉害,是否怀疑过模型?
遇到这种问题以后,首先要做的就是确定模型的建立的合理性,依据是哪些?如果模型是合理的,那么比较重要的一点,就是需要将数据进行分析。
数据建模中的许多数据都是实际数据,而模型,是一种标准化。
实际数据放在模型中去验证,很多都是有问题。出现这些问题的原因,不是模型错误,而是数据不一定有效。
下面就举几种数据不一定有效的情况:
第一种情况是由于某些原因造成的缺少数据;
第二种情况是由于人为的一些原因造成的数据错误;
第三种情况是由于数据采集过程中,不恰当采集,造成的脏数据。
还有很多种情况,就不在这里细说。
遇到这样的事情,首先要做到的就是剔除掉无效数据,然后再论文中说明,为什么要剔除这些数据,然后再验证模型的合理性。
扫描下方二维码
阅读完整原文
并与作者交流