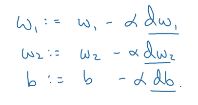第一课 神经网络与深度学习 第二周 神经网络基础（已完结（虽然有坑））
视频地址
二分分类
怎么说，第一段话就颠覆了我的想象，遍历m个样本不需要用for循环
这里是介绍了图片的预处理，将图片切分为rgb三个颜色空间（这个我熟），然后将所有的分别将三幅单通道图片的所有像素排列为一个列向量，这样得到三个列向量
这里讲的是一些变量名称的约定
我们的训练样本为x，其经过神经网络处理后输出的结果为y，y的取值为0或1
一个数据规模为m的数据集，可以用ppt中第二行那样的形式表示
在实际使用中，我们常将特征向量作为列向量堆叠到数据集矩阵中（老师说这样有好处），将输出的y变成一个1×m的行向量（那这个中间的这个计算的矩阵是怎么操作的？？？）
logistic回归
这是一个学习算法，用在监督学习问题中，输出y的标签是0或者1时
需要一个算法，能够给出一个预测值（一个概率），当输入特征x满足条件时，y就是1
然后就开始讲一些我听不懂的东西了
老师首先说，对于logistic回归，我们给其中输入训练数据集x和系数w,b
一种可能的计算方法是线性的计算
但是这种计算的弊端很明显，我们算出来的y尖的值可能为负数或者大于1，这对于概率来说是没有任何意义的
然后引入了一个sigmiod函数（？？？），使计算式变为
这个应该是sigmoid函数的图像，他能够将x轴上的实数平滑的投影到0-1的区间内，解决了线性计算式概率会不符合规定的问题
这里是sigmoid函数的表达式
所以我们的任务就是得到较好的w和b
这里是另外的符号定义，老师说不会用
logistic回归损失函数
上一个视频介绍的是logistic回归的模型，为了训练这个模型，得到参数w和b，我们需要定义一个成本函数
老师首先讲上个视频的函数
为了让模型通过学习调整参数，要给一个m个样本的数据集
我们希望得到的w和b能够使预测值（模型算出，通过sigmoid函数作用于线性计算式得到的）与实际值（人手动标记的）接近
其中每个样本x都有其对应的y尖
接下来给出了一个损失函数（误差函数），其可以衡量算法的运行情况
其中一种可能的损失函数是
在学习这些参数的时候，会发现之后讨论的优化问题，会变成非凸的（听不懂），最后会得到很多个局部最优解，对于梯度下降法，可能得不到全局最优解
所以大家都不用，所以我们看下一种
我们通过定义这个损失函数，来衡量你的预测输出值y尖和y的实际值有多接近
由于上一种不好用，老师定义了另外一个损失函数，并同时解释了这个损失函数为什么行
老师举了两个极限的例子，分别是实际y=0时和实际y=1时的情况
y=1时，损失函数变为
我们的目的是让损失函数尽可能小，即y尖尽可能大，所以y尖会接近1，接近我们实际的y=1
y=0时，损失函数变为
损失函数尽可能小时，1-y尖要尽可能大，那么y尖会接近0，接近我们实际的y=0
当y与y尖接近时，损失函数很小，那么我们说这个损失函数是好的，这就是我们为什么用上面那个损失函数
下面才是我们所需要的成本函数
他衡量的是在全体训练样本上的表现（所以就是将损失函数求和）
梯度下降法
我们在上个视频中知道了logistic回归函数中有两个重要的参数：w和b，但是我们并没有说明如何得到这两个参数
所以这节课，我们将用梯度下降法来逼近这两个参数的最优取值
这里老师将成本函数的图像画了出来，根据这个图像，我们很直观的能够看到，对于这个成本函数而言，在数次迭代后，是一定有一组(w,b)，使得J(w,b)取到最小值，也就是我们需要的参数w和b的值
然后关于如何取w和b的初值，老师说对于logistic回归而言，任意的初始化方式都有效，一般我们初始化为0，当然随机数初始化也是可行的，但是不推荐
这里相当于变相的解释了，对于logistic回归，我们为什么要使用这个特定的成本函数
接下来解释梯度下降得到最优解的原理
老师为了简化解释过程，画了一个二维的图像
这个图像的最小值，相当于三维图像的最低点，这里的横轴是w，为了找到这个w，我们需要进行迭代，迭代的方式老师直接给出了，w=w-α×J的导数（α是学习率，老师在后面会进行解释），同时也进行了解释
假设我们的w此时在最小值的右边，我们需要往左移动，显然，这里函数的导数为正，那么经过迭代之后，w会减小，朝着我们目标方向前进
w在最小值的左边时也是同理
在最后，老师给出了我们在进行梯度下降时实际进行的操作，就是上面两个迭代的过程，关于这个符号，老师在这里没有使用偏导的符号，而是直接使用了一元函数求导的d，但是这无关紧要
导数
看这个标题，是数学课了
但是老师说听不懂也没关系哈哈哈哈哈哈
这是到目前为止唯一一集不用脑子就能听懂的课
老师说了斜率的定义，然后讲导数就是斜率，然后说了几个导数的表示方式
更多导数的例子
好像还是数学课？
完全是摆烂不想听的东西
截两张ppt，就这样
计算图（computation graph）
（？这集在讲什么）
老师说一个神经网络的计算都是按照前向或者反向传播过程来实现的，我们首先计算出神经网络的输出，紧接着进行一个反向传输操作，用反向传出的计算对应的梯度，导数，然后就直接是例子
这个例子中，老师讲了从输入计算出成本函数的过程，下一个视频要讲如何利用这个输出来计算我们所需要的导数（为什么可以计算出来？）
计算图的导数计算
这我看完，不就是链式求导？高数下警告！
散了吧散了吧，就是链式求导
但是求导可以让我们知道如何最快的下降到我们需要的最优解，这对于缩短训练时间有重要意义
logistic回归中的梯度下降法
这集主要介绍如何计算偏导数来实现logistic回归的梯度下降法
这里需要做一个解释（感谢弹幕）
这里的这个z的表达式，实际上w和x都是一个矩阵，这才会有后面z=(w1x1)+(w2x2)+b的这个式子
这里也需要作说明，这个损失函数L对a求偏导后（默认log的底数是e自然对数），就是
然后到了这张ppt，我认为也需要解释
dz=dL/dz=(dL/da)×(da/dz)
然后σ函数的表达式我们是已知的（自己翻前面的内容），求导之后直接等于a(1-a)（自己算！）
这是我们最后的ppt，计算出dw1，dw2，db（动笔算算吧）后，我们就可以更新我们的w1，w1和b（当然学习率还不知道是啥，慢慢来吧）
m个样本的梯度下降
这个视频讲的是如何将上个视频提到的方法应用到m个样本的训练集中
成本函数是损失函数的值的平均值，然后对于导数，可以是分开的求导之后再求和
根据上一个视频的推导，我们如果要完成一步梯度下降，对于一个二维向量，我们需要对于全局成本函数计算两个导数，分别对这两个特征进行求导（当然还有db），即求出下面三个值，然后带入给出的公式中，进行一步梯度下降
接下来需要逐行解释ppt，因为说实话有点听不懂
第一行是初始化，之前说对于logistic回归，我们可以任意初始化（随机初始化也可以，但不支持），所以这里所有值初始化为0
对于一个m个样本的训练集，我们需要遍历所有的样本（这里用的还是显式遍历，隐式遍历会在后面讲到），然后依次计算z，a，J，dz，dw1，dw2，db（假设一个样本只有两个特征）
然后计算平均值
之后进行更新，更新w1，w2，b的值
做一个说明，老师说我们在深度学习算法中若显式的使用for循环，会使算法很低效，我们需要完全不用显式for循环，对应的，有一门向量化技术，可以解决掉这些显式的for循环
这节课和上节课之间千万不能休息啊！（不然就会重新学一遍上一集的）
向量化
好耶第一个内容就是讲解什么是向量化
看完好像觉得，向量化就是调用了python里的一个库函数然后实现了，多线程实现了加速计算
这里是写了实际的代码来作为解释
然后老师说，只要能不用显式for循环，那就不要用
向量化的更多例子
这里还是朴素方法和库函数计算方法的比较
左边是朴素的向量v中每一个分量的指数运算，右边是直接一行代码就能解决问题，然后老师还举了几个numpy中的多个库函数，log，abs，maximum，平方（v**2）等
原本ppt上是标准的计算logistic回归导数的程序，然后板书是经过numpy优化后的版本
第一行初始化的时候，我们可以直接将dw初始化为一个全为0的向量，然后下面的两步优化可以直接用矩阵的计算来进行
向量化logistic回归
这节课将如何向量化实现logistic回归，然后首先讲如何使用向量来计算z=wT×x+b
我们让w为一个n×1的矩阵，x为一个n×m的矩阵（将每一个样本的特征值按照列进行排列，并排放到一起），b为一个实数，我们需要的z也是一个1×m的矩阵，这样当w的转置×X矩阵时，我们最后的结果就是一个1×m矩阵，就是我们需要的结果
最后在python中，这些操作合成了一句话，就是Z=np.dot(w.T,X)+b
最后的一步是计算a=σ(Z)，也可以直接用向量的方法计算
向量化logistic回归的梯度输出
看完只觉得大无语，说是不用for循环，只不过是把循环封装到了矩阵的运算之中，将我们大量的数据注入矩阵，利用矩阵的运算一次性算出我们的所有值
反正经过矩阵的构造，我们可以一次性计算我们需要的很多值
这里说的就是将之前用for循环的代码如何修改为不需要for的代码，但是需要注意的是，我们这里只做了一次迭代，如果需要多次的迭代，我们还是需要for循环，而且这种for循环是无法避免的
python中的广播
如题，这个视频主要讲的是python中的广播，类似于自动扩展作用范围（？）
老师首先抛出了一个例子，这是对于四种不同食物的一个卡路里来源表，问我们能不能不用for循环来计算出四种食物中的碳水化合物提供的卡路里的占比
md看到一半不禁感叹python真tm是一门神奇的语言
下面是实现上述描述的代码就两行，很快啊，不讲武德，然后老师说要讲另外的例子
比如说这个
离谱啊真离谱
我个人认为是不用记的，到时候要用的时候直接试一下就好了
这又是另外的例子，也基本上是最终的运算规律
关于python_numpy向量的说明
这里主要是讲一些注意事项，我到目前为止还没有接触过python，所以对老师说的这些东西还不是很有感触
有一点，在初始化时，一定要将向量初始化为1×5或者5×1这种，图片中的下面两种初始化方法是推荐的
Jupyter ipython笔记本的快速指南
啊，啥也没讲，就讲了一下他的这个ipython笔记本，没了
（选修）logistic损失函数的解释
我们在之前的视频中，并没有解释为什么要使用这个损失函数，所以这个视频就解释了，为什么要使用这样的损失函数
我们在之前的定义中，y尖是一个概率，由z经σ函数运算后，映射到0-1之间作为概率（后面写了σ函数的式子）
约定说y尖，是在给定的x的条件下，y=1的概率
所以
y=1时，P(y|x)=y尖
y=0时，P(x|x)=1-y尖
这里最上面两个式子是之前的条件概率的式子，然后第一个手写的式子是将这两个式子合并的结果（gay率论警告），下面绿色和紫色的式子是对这个合并的解释，然后对于这个log运算的解释，我的理解是
log在大于0范围内严格递增，那么我们只要得到了损失函数取对数之后的最大值，我们就能知道其还原之后的值，然后我们的损失函数是该log值的相反数，这样我们就能通过求原log值最大时，求得最小的损失函数
投降投降，这一张ppt是完全不懂的，全部是概率论的知识，给自己留个坑吧
视频地址在这里
写在后面
首先感谢你看到这里，这个博客我前前后后写了将近一个多星期的时间，中间有概率论，有电路，有大物等等科目的阻碍，还莫名其妙的当上了部长（没人认识我，我根本不保密哈哈哈哈哈哈），学了这么久也才学了一个星期的内容，但是我相信我可以坚持下去的！
怎么说，这是我第一次接触深度学习，原来也就是将计算的过程看做一个函数，然后得到我们需要的结果，但是这其中有大量的关于概率论，微积分和线性代数相关的知识，如果你看到了这里并且没有系统性的学习过这三大数学（虽然我概率论也没学），抓紧机会好好学一下，学习是一个快乐的过程，isn’t it?