程序员的算法趣题Q29: 合成电阻的黄金分割比
目录
1. 问题描述
2. 解题分析
2.1 分割成两组
2.2 N=5时的分割例
2.3 阻值计算例
2.4 算法实现流程
3. 代码及测试
4. 后记
4.1 分割的洞见
4.2 另一种思路
1. 问题描述
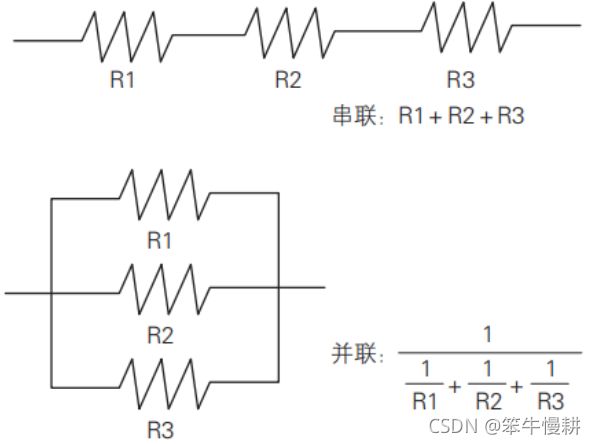
我们在物理课上都学过“电阻”,通过把电阻串联或者并联可以使电阻值变大或者变小。电阻值分别为 R1、R2、R3的 3 个电阻串联后,合成电阻的值为R1+R2+R3。同样3个电阻并联时,合成电阻的值则为“倒数之和的倒数”。如下图所示:
现在假设有n个电阻值为1 Ω的电阻。组合这些电阻,使总电阻值接近黄金分割比1.6180339887…。举个例子,当 n = 5 时,如果下图这样组合,则可以使电阻值为 1.6。
问题:求n=10时,在所有可能的电阻网络中,所得到的电阻中最接近黄金分割比的数值,精确到小数点后10位。
2. 解题分析
2.1 分割成两组
本题解的最关键的insight是对于任何电阻网络,总是可以把它分割成两个组,两个组内部的拓扑结构任意,两个组之间或串联或并联。然后,每个组又可以同样继续分割下去,因此本题可以用动态规划的策略来解决。详细分析过程如下。
2.2 N=5时的分割例
2.3 阻值计算例
以下为到N=4为止的笔算计算例。
2.4 算法实现流程
3. 代码及测试
# -*- coding: utf-8 -*-
"""
Created on Wed Sep 15 07:13:17 2021
@author: chenxy
"""
import sys
import time
import datetime
import math
# import random
from typing import List
# from queue import Queue
# from collections import deque
import itertools as it
F = dict()
F[1] = {1}
golden_ratio = (math.sqrt(5) + 1)/2
def parallel(x,y):
return x*y/(x+y)
def findValueClosest2GoldenRatio(N):
for k in range(2,N+1):
valueSet = set()
for l in range(1,k//2+1):
g1_size = l
g2_size = k - l
for e1 in F[g1_size]:
for e2 in F[g2_size]:
valueSet.add(e1+e2)
valueSet.add(parallel(e1, e2))
F[k] = valueSet
# Find the value closest to golden ratio
valueWithMinDiff = 0
minDiff = golden_ratio
for v in F[N]:
diff = abs(v-golden_ratio)
if diff < minDiff:
minDiff = diff
valueWithMinDiff = v
return valueWithMinDiff, F[N]
N = 10
tStart = time.perf_counter()
valueWithMinDiff, valueSet = findValueClosest2GoldenRatio(N)
tCost = time.perf_counter() - tStart
print('golden_ratio={0:11.10f}, valueWithMinDiff={1:11.10f}, tCost= {2:6.3f}(sec)'.format(golden_ratio,valueWithMinDiff,tCost))
print('Totally there are {0} kinds value for N = {1} element circuit network'.format(len(valueSet),N))
运行结果:
golden_ratio=1.6180339887, valueWithMinDiff=1.6181818182, tCost= 0.003(sec)
Totally there are 3158 kinds value for N = 10 element circuit network
由以上结果还可以看出,在N=10时总共有3158中可能的电阻值。那可能的拓扑结构数至少不小于这个数。因为有些不同的拓扑结构的电阻值可能是相同的。
4. 后记
4.1 分割的洞见
这道题是到目前为止看完题目后觉得最没有头绪的题目。觉得无从下手。原书中给的提示没看懂要说啥,即便做完了这道题目再回头看依然没有看懂要说啥。“偷看”了几个网友的解答,也没有看出什么头绪(只上代码很难说有什么参考意义,这种问题直接读代码很难读懂)。在程序员的算法趣题:Q29 合成电阻的黄金分割比(Java版)_lanying100的博客-CSDN博客读到“分割成两组”的思路,一开始也没有想明白,最后终于想明白了,觉得这个洞见确实妙极!想通了这一点后面就水到渠成了。最后,希望本文的解说能够让人更容易理解一些。
4.2 另一种思路
一开始我按照另外一种思路走,即把串联和并联看作是两种运算符,再加上括号,这样任何一种电路网络都可以表示为一个由若干个1为操作数,包含以上两种运算符以及括号的“算术”表达式。遍历所有可能的 “算术”表达式然后评估表达式的值即可。
但是在“遍历所有可能的“算术表达式”这点上卡壳了。由于括号的位置拜访的自由度很高,而且还存在深度嵌套的情况,对于这种非常“非结构性”的东西要遍历没有想到什么好办法,暂时只好放弃了。但是觉得这个把问题转变为算术表达式求值的思路还是不错的。
上一篇:Q28: 社团活动的最优分配方案
下一篇:Q30: 插线板连接方式
本系列总目录参见:程序员的算法趣题:详细分析和Python全解