ORB_SLAM2中基础矩阵F求解的原理及源码分析

1. 基础矩阵的定义

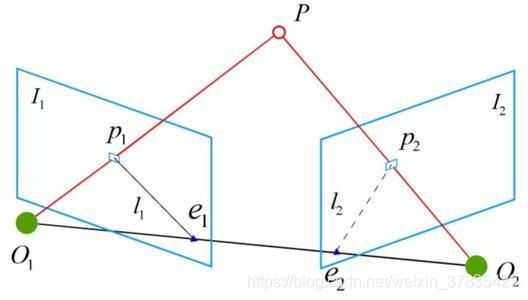
如图所示是对极几何约束关系图，图中$O_1,O_2$分别表示相机的两个位姿，平面$I_1,I_2$分别表示对应的投影平面，$P$点为三维环境中的一个位置点，$p_1,p_2$分别表示$P$点在两个投影平面上的投影．假设位姿$O_2$相对于位姿$O_1$的旋转变换矩阵为$\mathbf{R}$、平移向量为$\mathbf{t}$，相机的内参为$\mathbf{K}$，则根据相机投影关系可得:
$$s_1{\mathbf{p}}_1=\mathbf{K}\mathbf{P},s_2{\mathbf{p}}_2=\mathbf{K}(\mathbf{R}\mathbf{P}+\mathbf{t})\text{\hspace{1em}(1)}$$
令${\mathbf{x}}_1=\mathbf{P}/s_1,{\mathbf{x}}_2=(\mathbf{R}\mathbf{P}+\mathbf{t})/s_{\mathrm{２}}$(懂相机投影知识的应该都知道，其实${\mathbf{x}}_1,{\mathbf{x}}_2$就是点$\mathbf{P}$在相机的归一化平面上的投影)，可得:
$${\mathbf{x}}_1={\mathbf{K}}^{-1}{\mathbf{p}}_1,{\mathbf{x}}_2={\mathbf{K}}^{-1}{\mathbf{p}}_2\text{\hspace{1em}(2)}$$
将(2)式带入(1)式消去$\mathbf{P}$可得:
$$s_2{\mathbf{x}}_2=\mathbf{R}{s}_1{\mathbf{x}}_1+\mathbf{t}\text{\hspace{1em}(3)}$$
等式(3)两边同时乘以$\mathbf{t}$的反对成矩阵${\mathbf{t}}^{\hat{}}$可得:
$${\mathbf{t}}^{\hat{}}{s}_2{\mathbf{x}}_2={\mathbf{t}}^{\hat{}}\mathbf{R}{s}_1{\mathbf{x}}_1\text{\hspace{1em}(4)}$$
等式(4)两边同时乘以${\mathbf{x}}_2^T$可得:
$$s_2{\mathbf{x}}_2^T{\mathbf{t}}^{\hat{}}{\mathbf{x}}_2=s_1{\mathbf{x}}_2^T{\mathbf{t}}^{\hat{}}\mathbf{R}{\mathbf{x}}_1\text{\hspace{1em}(5)}$$
由于${\mathbf{t}}^{\hat{}}{\mathbf{x}}_2$的结果是一个垂直于$\mathbf{t}$和${\mathbf{x}}_2$的向量，因此向量${\mathbf{x}}_2$与该垂向量的点积为0，因此式(5)可变为:
$${\mathbf{x}}_2^T{\mathbf{t}}^{\hat{}}\mathbf{R}{\mathbf{x}}_1=0\text{\hspace{1em}(6)}$$
将公式(2)带入公式(6)可得:
$${\mathbf{p}}_2^T{\mathbf{K}}^{-T}{\mathbf{t}}^{\hat{}}\mathbf{R}{\mathbf{K}}^{-1}{\mathbf{p}}_1=0\text{\hspace{1em}(7)}$$
令:$\mathbf{E}={\mathbf{t}}^{\hat{}}\mathbf{R}$和$\mathbf{F}={\mathbf{K}}^T{\mathbf{t}}^{\hat{}}\mathbf{R}{\mathbf{K}}^{-1}$可得:
$${\mathbf{x}}_2^T\mathbf{E}{\mathbf{x}}_1={\mathbf{p}}_2^T\mathbf{F}{\mathbf{p}}_1=0\text{\hspace{1em}(8)}$$
式中$\mathbf{E}$即为本质矩阵，$\mathbf{F}$即为基础矩阵.

2. 基础矩阵的求解(八点法)

我们假设存在一对匹配的像素点${\mathbf{p}}_1=[u_1,v_1]$，${\mathbf{p}}_2=[u_2,v_2]$，则根据公式(8)可得:
$$(u_1,v_1,1)\left(\begin{array}{ccc}{f}_1& f_2& f_3\\ f_4& f_5& f_6\\ f_7& f_8& f_9\end{array}\right)(u_2,v_2,1{)}^T=0\text{\hspace{1em}(9)}$$
令: $\mathbf{F}=[f_1,f_2,f_3,f_4,f_5,f_6,f_7,f_8,f_9{]}^T$，则可将公式(9)转换成与$\mathbf{F}$有关的线性表达:
$$[u_1{u}_2,u_1{v}_2,u_1,v_1{u}_2,v_1{v}_2,v_1,u_2,v_2,1]\cdot \mathbf{F}=0\text{\hspace{1em}(10)}$$
从上述推导可以看出来，每一对匹配点都可以建立一个如公式(10)所示的与基础矩阵有关的齐次线性方程．基础矩阵$\mathbf{F}$有9个未知数，因此需要9对匹配点来求解，但基础矩阵又有一个重要的性质是它具有尺度等价性，因此实际只有8个未知数，因此可以用8对匹配点来求解基础矩阵，这就是八点法．因此可以根据8对匹配点建立如下齐次线性方程组:
$$\left(\begin{array}{c}{u}_1^1{u}_2^1,u_1^1{v}_2^1,u_1^1,v_1^1{u}_2^1,v_1^1{v}_2^1,v_1^1,u_2^1,v_2^1,1\\ u_1^2{u}_2^2,u_1^2{v}_2^2,u_1^2,v_1^2{u}_2^2,v_1^2{v}_2^2,v_1^2,u_2^2,v_2^2,1\\ .......................................................\\ u_1^7{u}_2^7,u_1^7{v}_2^7,u_1^7,v_1^7{u}_2^7,v_1^7{v}_2^7,v_1^7,u_2^7,v_2^7,1\\ u_1^8{u}_2^8,u_1^8{v}_2^8,u_1^8,v_1^8{u}_2^8,v_1^8{v}_2^8,v_1^8,u_2^8,v_2^8,1\end{array}\right)\cdot \mathbf{F}=0\text{\hspace{1em}(11)}$$
求解齐次线性方程组(11)的常用方法是利用SVD求解，经过SVD分解后，方程组的解即为最小奇异值对应的${\mathbf{V}}^T$的列向量，详细求解过程可参考 https://blog.csdn.net/youngpan1101/article/details/54574130．至此完成基础矩阵的求解.

3. 代码解析

求解流程

/**
 * @brief 计算基础矩阵，假设场景为非平面情况下通过前两帧求取Fundamental矩阵，得到该模型的评分
 * Step 1 将当前帧和参考帧中的特征点坐标进行归一化
 * Step 2 选择8个归一化之后的点对进行迭代
 * Step 3 八点法计算基础矩阵矩阵
 * Step 4 利用重投影误差为当次RANSAC的结果评分
 * Step 5 更新具有最优评分的基础矩阵计算结果,并且保存所对应的特征点对的内点标记
 * 
 * @param[in & out] vbMatchesInliers          标记是否是外点
 * @param[in & out] score                     计算基础矩阵得分
 * @param[in & out] F21                       从特征点1到2的基础矩阵
 */
void Initializer::FindFundamental(vector &vbMatchesInliers, float &score, cv::Mat &F21)
{
    // 计算基础矩阵,其过程和上面的计算单应矩阵的过程十分相似.

    // Number of putative matches
	// 匹配的特征点对总数
    // const int N = vbMatchesInliers.size();  // !源代码出错！请使用下面代替
    const int N = mvMatches12.size();
    // Normalize coordinates
    // Step 1 将当前帧和参考帧中的特征点坐标进行归一化，主要是平移和尺度变换
    // 具体来说,就是将mvKeys1和mvKey2归一化到均值为0，一阶绝对矩为1，归一化矩阵分别为T1、T2
    // 这里所谓的一阶绝对矩其实就是随机变量到取值的中心的绝对值的平均值
    // 归一化矩阵就是把上述归一化的操作用矩阵来表示。这样特征点坐标乘归一化矩阵可以得到归一化后的坐标

    vector vPn1, vPn2;
    cv::Mat T1, T2;
    Normalize(mvKeys1,vPn1, T1);
    Normalize(mvKeys2,vPn2, T2);
	// ! 注意这里取的是归一化矩阵T2的转置,因为基础矩阵的定义和单应矩阵不同，两者去归一化的计算也不相同
    cv::Mat T2t = T2.t();

    // Best Results variables
	//最优结果
    score = 0.0;
    vbMatchesInliers = vector(N,false);

    // Iteration variables
	// 某次迭代中，参考帧的特征点坐标
    vector vPn1i(8);
    // 某次迭代中，当前帧的特征点坐标
    vector vPn2i(8);
    // 某次迭代中，计算的基础矩阵
    cv::Mat F21i;

    // 每次RANSAC记录的Inliers与得分
    vector vbCurrentInliers(N,false);
    float currentScore;

    // Perform all RANSAC iterations and save the solution with highest score
    // 下面进行每次的RANSAC迭代
    for(int it=0; itscore)
        {
            //如果当前的结果得分更高，那么就更新最优计算结果
            F21 = F21i.clone();
            vbMatchesInliers = vbCurrentInliers;
            score = currentScore;
        }
    }
}

八点法计算基础矩阵(此部分对应第二节 基础矩阵的求解(八点法))

/**
 * @brief 根据特征点匹配求fundamental matrix（normalized 8点法）
 * 注意F矩阵有秩为2的约束，所以需要两次SVD分解
 * 
 * @param[in] vP1           参考帧中归一化后的特征点
 * @param[in] vP2           当前帧中归一化后的特征点
 * @return cv::Mat          最后计算得到的基础矩阵F
 */
cv::Mat Initializer::ComputeF21(
    const vector &vP1, //归一化后的点, in reference frame
    const vector &vP2) //归一化后的点, in current frame
{
	//获取参与计算的特征点对数
    const int N = vP1.size();

	//初始化A矩阵
    cv::Mat A(N,9,CV_32F); // N*9维

    // 构造矩阵A，将每个特征点添加到矩阵A中的元素
    for(int i=0; i(i,0) = u2*u1;
        A.at(i,1) = u2*v1;
        A.at(i,2) = u2;
        A.at(i,3) = v2*u1;
        A.at(i,4) = v2*v1;
        A.at(i,5) = v2;
        A.at(i,6) = u1;
        A.at(i,7) = v1;
        A.at(i,8) = 1;
    }

    //存储奇异值分解结果的变量
    cv::Mat u,w,vt;

	
    // 定义输出变量，u是左边的正交矩阵U， w为奇异矩阵，vt中的t表示是右正交矩阵V的转置
    cv::SVDecomp(A,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);
	// 转换成基础矩阵的形式
    cv::Mat Fpre = vt.row(8).reshape(0, 3); // v的最后一列

    //基础矩阵的秩为2,而我们不敢保证计算得到的这个结果的秩为2,所以需要通过第二次奇异值分解,来强制使其秩为2
    // 对初步得来的基础矩阵进行第2次奇异值分解
    cv::SVDecomp(Fpre,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);

	// 秩2约束，强制将第3个奇异值设置为0
    w.at(2)=0; 
    
    // 重新组合好满足秩约束的基础矩阵，作为最终计算结果返回 
    return  u*cv::Mat::diag(w)*vt;
}

利用重投影误差为当次RANSAC的结果评分

/**
 * @brief 对给定的Fundamental matrix打分
 * 
 * @param[in] F21                       当前帧和参考帧之间的基础矩阵
 * @param[in] vbMatchesInliers          匹配的特征点对属于inliers的标记
 * @param[in] sigma                     方差，默认为1
 * @return float                        返回得分
 */
float Initializer::CheckFundamental(
    const cv::Mat &F21,             //当前帧和参考帧之间的基础矩阵
    vector &vbMatchesInliers, //匹配的特征点对属于inliers的标记
    float sigma)                    //方差
{
	// 获取匹配的特征点对的总对数
    const int N = mvMatches12.size();

	// Step 1 提取基础矩阵中的元素数据
    const float f11 = F21.at(0,0);
    const float f12 = F21.at(0,1);
    const float f13 = F21.at(0,2);
    const float f21 = F21.at(1,0);
    const float f22 = F21.at(1,1);
    const float f23 = F21.at(1,2);
    const float f31 = F21.at(2,0);
    const float f32 = F21.at(2,1);
    const float f33 = F21.at(2,2);

	// 预分配空间
    vbMatchesInliers.resize(N);

	// 设置评分初始值（因为后面需要进行这个数值的累计）
    float score = 0;

    // 基于卡方检验计算出的阈值
	// 自由度为1的卡方分布，显著性水平为0.05，对应的临界阈值
    // ?是因为点到直线距离是一个自由度吗？
    const float th = 3.841;

    // 自由度为2的卡方分布，显著性水平为0.05，对应的临界阈值
    const float thScore = 5.991;

	// 信息矩阵，或 协方差矩阵的逆矩阵
    const float invSigmaSquare = 1.0/(sigma*sigma);


    // Step 2 计算img1 和 img2 在估计 F 时的score值
    for(int i=0; ith)
            bIn = false;
        else
            // 误差越大，得分越低
            score += thScore - chiSquare1;

        // 计算img2上的点在 img1 上投影得到的极线 l1= p2 * F21 = (a1,b1,c1)
        const float a1 = f11*u2+f21*v2+f31;
        const float b1 = f12*u2+f22*v2+f32;
        const float c1 = f13*u2+f23*v2+f33;

        // 计算误差 e = (a * p2.x + b * p2.y + c) /  sqrt(a * a + b * b)
        const float num1 = a1*u1+b1*v1+c1;
        const float squareDist2 = num1*num1/(a1*a1+b1*b1);

        // 带权重误差
        const float chiSquare2 = squareDist2*invSigmaSquare;

        // 误差大于阈值就说明这个点是Outlier 
        if(chiSquare2>th)
            bIn = false;
        else
            score += thScore - chiSquare2;
        
        // Step 2.5 保存结果
        if(bIn)
            vbMatchesInliers[i]=true;
        else
            vbMatchesInliers[i]=false;
    }
    //  返回评分
    return score;
}

参考

<<视觉slam14讲>>
https://github.com/raulmur/ORB_SLAM2
https://github.com/electech6/ORB_SLAM2_detailed_comments
https://zhuanlan.zhihu.com/p/61614421