大数据毕业论文：基于大数据的金融量化分析2021-07

大数据毕业论文：基于大数据的金融量化分析

已毕业，留念，仅供参考。

效果图：

3 运行设计
3.1用户界面

图3-1 运行界面
Finanical.py 获取股票基础数据
view.py 股票价格走势可视化
viewR.py 股票日收益率可视化
viewend.py 股票收益率密度正态分布可视化
analysis_data.py 股票数据分析
analysis_end_data.py 优化组合个股票权重分析计算及可视化
Analysis_view_one.py 股票优化组合模拟收益情况可视化
end.py 投资组合有效前沿可视化

分割

信息工程学院本科生毕业设计说明书

题目： 基于大数据的金融量化分析

姓 名：
学 号：
专 业： 数据科学与大数据
班 级：
指 导 教 师：

摘 要

随着网络科技的迅速发展，现在大数据技术几乎被应用到各行业里，同时量化投资的分析方式也因为大数据的影响而逐渐发生变化。量化分析离开数据样本的束缚就是归功于大数据，样本中的海量数据，甚至整个样本数据的研究逐渐成为金融学者的共同认识，我们的一些交易模式也发生了变化。使用计算机建立数学模型，利用计算机语言进行可视化，进行理性判断而不是人类的思考,可以更有效的实现准确的金融资产定价更直观的预测投资机遇。给我们带来更优化的收益。
此项目系统编程在Windows环境下，用python语言编程，通过pyCharm开发工具，创建pro接口在Tushare中完成对金融股票数据的采集，将数据存储于csv文件中，进行数据分析以及预处理，最后通过数据可视化展示成果。

关键词：大数据分析； 数据可视化；金融； 量化投资

目 录

1 系统概述 1
1.1 设计目的 1
1.2 设计思路 1
1.3 系统需求分析 3
1.4 开发环境 3
1.5 运行环境 3
2 总体设计 4
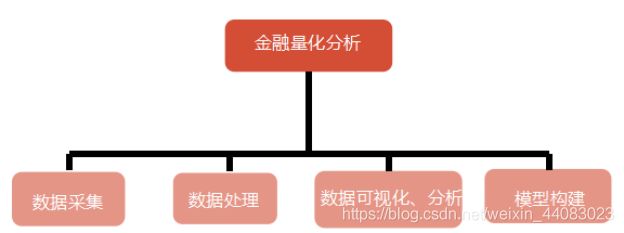
2.1 系统结构 4
2.2 模块功能设计 4
2.2.1 数据采集功能 4
2.2.2 数据预处理功能 6
2.2.3 数据分析及可视化功能 7
2.2.4 模型构建及可视化功能 12
3 运行设计 16
3.1运行界面 16
3.2 运行代码 16
4 系统测试 25
4.1 功能测试 25
4.2 稳定性测试 25
参考文献 26

1 系统概述
1.1 设计目的
金融科技正在越来越深刻地影响量化投资领域。而量化投资依赖于程序进行决策，减少了人的不理性决策可以避免人性的诸多弱点，并且可以从量化的角度分散化投资风险。
1.2 设计思路
在量化投资领域，最流行的编程语言就是Python，主要原因是Python简单易上手，并且有诸多数据分析、可视化以及统计建模的包可供我们使用。本设计使用Python进行量化投资，我将从数据获取、数据清洗、数据可视化、构造有效投资组合几个方面介绍Python在量化交易中的应用。
1.2.1 知识储备
（1）量化投资:利用计算机技术并且采用一定的数学模型去实践投资理念，实现投资策略的过程。
（2）在股票投资领域，我们其实关注的并不是股票的价格，而是股票收益率。股价与股票收益率关系，股票日度收益率公式：
但是在实际应用中，这种方式需要的计算量比较大，因此我们一般使用：
1.2.2数据采集
股票交易数据的获取有诸多种方式，一些大型数据商如万得（Wind）会提供非常详细、实时更新的股票交易数据，我们也可以通过爬虫等方式获取股票交易数据。但是对于初学者而言，这些方法要么费时间，要么需要付费进行购买。这里，我使用一个国内免费、开源的财经数据接口包：Tushare，它可以方便快捷地帮助我们获取所需要的数据。
1.2.3 数据清洗
获得股票数据之后，需要对其进行清洗，首先查看一下数据是否存在缺失值（因为股票有时候会被停牌有的数据存在少量缺失值,有则可以用线性插值法
常见的清洗方法，将数据清洗定义为处理异常值和缺失值。
异常值，指的是数据中不合理的值，通常情况下，异常值的取值比较极端。异常值影响我们发现规律，我们需要分析后并去掉它们的影响。对于异常值，量化中常见的处理方法是截尾。
1.2.4 数据可视化
（1）Matplotlib基础图形绘制：-plt.plot() : 绘制图形；–plt.show()：图形显示；
（2）pandasn内置图形可视化
（3）Seaborn包
进行股票历史价格走势；日度收益率；日收益率波动情况；日收益率分布情况；各股票收益率正态分布图等的数据可视化。
1.2.5 数据分析
（1）基于最优夏普比率构建股票投资组合。计算投资组合的收益与方差。
假设两种风险资产的期望收益分别为 E(r1)，E(r2) ，标准差分别为 σ1，σ2 ，协方差为σ12 ，投资在风险资产1上面的比重为W1 ，投资在风险资产2上面的比重为W2，那么投资组合（Portfolio）的期望收益率为：
投资组合（Portfolio）的方差为：
如果股票的数量更多用矩阵的形式来写会比较清楚直观：
E®：五只股票的均值向量。Var®：五只股票的协方差矩阵。W：权重向量。
（2）经典的金融学理论认为我们要寻找最优夏普比率（Sharp ratio）的投资组合，因为它衡量了承担一单位风险带来的收益补偿，夏普比率定义如下：
（3）有效前沿是可行集的一条包络线，他表示了在不太够的风险条件下能够给投资者带来的最高预期收益率，或者在不同预测收益条件下能够给投资者带来的最低波动率（风险）其实有效前沿就是求解以下最优条件:

（4）将无风险资产纳入投资组合中，也就意味着投资者可以按照无风险利率借入或者借出任何数量的资金， 这样就引出了资产市场线。
其中，Rp表示无风险利率，E(Rm)与σM分别代表了资本市场线与有效前沿的切点所对应的投资组合（即市场组合）预期收益率与收益波动率.
是资本市场线的斜率，也就是夏普比率。
1.3 系统需求分析
量化投资的优势:避免主观情绪、人性弱点和认知偏差，选择更加客观能同时包括多角度的观察和多层次的模型。及时跟踪市场变化,不断发现新的统计模型，寻找交易机会在决定投资策略后，能通过回测验证其效果。
现在金融领域的量化分析越来越受到理论界与实务界的重视，所谓金融量化，就是将金融分析理论与计算机编程技术相结合，使用计算机建立数学模型，利用计算机语言进行可视化，来判断而不是人们来思考,可以更有效的实现准确的金融资产定价更直观的预测投资机遇。给我们带来更多收益,也可以使我们避免减少更多的损失。
1.4 开发环境
（1）集成环境：Anaconda 集成了数据分析和机器学习中所需的所有环境
（2）pyCharm
（3）jupyter 基于浏览器的可视化开发工具
1.5 运行环境
运行环境硬件和软件配置
硬件条件:Core i5 4GB
软件条件: Windows 7、pyCharm、python。

2 总体设计
2.1系统结构

图2-1 模块结构图

2.2 模块功能设计
2.2.1 数据采集功能
Tushare是国内免费、开源的财经数据接口包，它可以方便快捷地帮助我们获取所需要的数据。本设计书中我们将在此接口中获得我们所需的股票数据。
（1）安装tushare包：pip install tushare

图2-2 tushare包安装
（2）创建账号获取接口 TOKEN

图2-3获取接口
（3）初始化接口
import tushare as ts
设置token，只需设置一次
ts.set_token(‘your token here’)
我的是：
ts.set_token(‘bc6edc25e6c0d0938accb6f0cb65130c1c0c1640a3900df5f042c893’)
#初始化接口
api = ts.pro_api()
（4）查询当前所有正常上市交易的股票列表，并导入表格
data=pro.query(‘stock_basic’,exchange=’’,list_status=‘L’,fields=‘ts_code,symbol,name,area,industry,list_date’)
data.to_excel(‘D:\Fun\data\data.xlsx’)

图2-4 所有股票基本数据
（5）根据列表选取你想要的股票数据
这里随机选取青岛啤酒600600.SH、美的000333.SZ、科华生物002022.SZ、恒瑞医药600276.SH和香飘飘603711.SH五家股票
（6）df = pro.daily（）此处我们需要收盘价，只需输出参数“close”即可。
将close数据命名防止混淆，trade_date改名为date,同时rename需要在后面加
inplace= ture确定
例如青岛啤酒股票数据：
qdpj=pro.query(‘daily’,ts_code=‘600600.SH’,start_date=‘20200101’,end_date=‘20210507’,
fields=‘trade_date,close’)
qdpj.rename(columns={‘close’:‘qdpj’,‘trade_date’:‘date’}, inplace = True)
输入Print(qdpj.head())
输出：

图2-5 青岛啤酒日收盘价
（7）将它们合并到一个DF数表里面，并且对该DF数表按照时间顺序进行排序。
DataFrame列表合并pd.merge(df1, def2,on=‘index’）:
alldata=pd.merge(pd.merge(pd.merge(pd.merge(qdpj,meidi,on=‘trade_date’),xpp,on=‘trade_date’),hksw,on=‘trade_date’),hryy,on=‘trade_date’)

图2-6 各股票日收盘价
2.2.2 数据预处理功能
因为股票有时候会被停牌有的数据存在少量缺失值，在本设计说明中我们使用pandas包进行数据清洗，检查是否缺失数据，进行缺失值处理。
（1）数据清洗
查看是否有空值异常值：
df.interpolate(method=“linear”,inplace=True)）
alldata.info()
非空状态显示为：non-null

图2-7 异常值情况
（2）数据存储
alldata.to_csv(‘D:\Fun\data\all.csv’)

图2-8存储数据
将标签换为中文：
alldata.rename(columns={‘qdpj’:‘青岛啤酒’,‘meidi’:‘美的’,‘hksw’:‘华科生物’,‘hryy’:‘恒瑞药业’,‘xpp’:‘香飘飘’}, inplace = True)
将数据存储：
alldata.to_csv(‘D:\Fun\data\allChinaTitle.csv’)
表2-1各股票日收盘数据

2.2.3 数据分析及可视化功能
数据预处理完成后，我们需要将股票数据计算分析，得到需要的数值，例如预期收益率、波动率（风险）、每只股票的平均收益率、波动率、协方差、年化收益波动率等等。利用matplotlib进行数据可视化显示股票走势，利用收益计算模型分析数据，将收益率波动可视化。
（1）股票历史价格趋势
将csv转为列表
读入csv文件数据并打开，创建list列表，遍历csv文各列数据将其存储到对应的标题列表中：
filename = ‘D:\Fun\data\all.csv’
with open(filename) as f:
reader = csv.reader(f)
创建列表：XX，XX = [],[]
dates,meidis,qdpjs,xpps,hksws,hryys = [],[],[],[],[],[]
遍历并存到列表中
for row in reader:
将date字符串以时间形式输出%Y%m%d ：
current_date = datetime.strptime(row[1], “%Y%m%d”)
dates.append(current_date)
因为数据存储到csv中读取数据是字符串形式，所以我们要将其转换为float或者int型，这里收盘价为小数点后两位，转为float ：
meidi = float(row[3])
meidis.append(meidi)
绘图
设置图大小
plt.figure(figsize=(17,12))
plt.plot(dates,meidis,label=“美的”)
在绘图时指定标签，在legend中不指定。通过label参数指定标签信息。该信息可以用来当做legend的图例标签。选best位置 ： plt.legend(loc=“best”)
局部设置 标题 设置fontproperties字体 Kaiti 中文楷体
plt.title(“股票价格历史走势”, fontproperties=“Kaiti”, fontsize=24)
设置x y轴的标签信息
plt.xlabel(“日期”,fontsize=20)
plt.ylabel(“股票价格”,fontsize=20)
图片保存或者运行
plt.savefig(‘D:\Fun\data\股票价格走势折线图.png’)
plt.show()

图2-9 股票价格历史走势
（2）股票日收益率波动情况
R=(r-r1)/r改成R=log®-log(r1)
df[‘Rqdpj’] = np.log(df[‘qdpj’]) - np.log(df[‘qdpj’].shift(-1))

图2-10股票日收益率
最后一行值为空，去除空值：
df.dropna(inplace=True)

图2-11数据空值示意图
①　绘制日收益率折线图

图2-12股票日收益波动图
②　绘制分布图
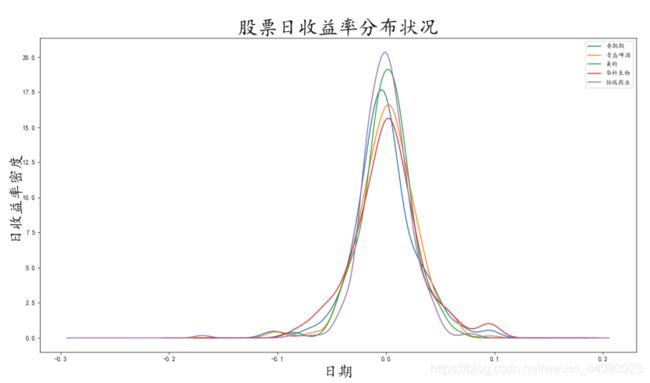
plt_dis=df[[‘香飘飘’,‘青岛啤酒’,‘美的’,‘华科生物’,‘恒瑞药业’] ].plot(figsize=(17,9),kind=“density”)

图2-13股票收益率分布图
③　绘制直方图
plt_hist=df.hist(figsize=(20,5),grid=False,layout =(1,5))

图2-14 各股票收益分布直方图
从上面两幅图来看，除了恒瑞医药之外，其他四只股票的日收益率都接近正态分布。
查看一下这五家股票的年化收益率：
#当然，实际投资中必须考虑股票停牌以及周末等非交易日
一年以252个交易日计算
df=df.mean()*252

图2-15 年化收益率
如上图所示，在我们考察的样本期内，青岛啤酒的年化收益率最高，为45%左右，华科生物紧随其后，为27%。而香飘飘最低，为-27%。当然，这是理想状况下的年化收益率，实际上必须考虑买入、卖出涉及的相关交易费用以及股票停牌等因素。不过结合市场实际状况来看，青岛啤酒的营收能力确实非常强悍！
接下来看一下五只股票的波动性和相关性。股票波动性意味着风险，用方差来衡量，我们使用DataFrame.var()获取五只股票的方差。
df=df.var()*252

图2-16 各股票收益波动值
从五只股票的波动状况来看，华科生物的股票波动性最大，对应的年化方差为0.25，也就是说购买华科生物股票对应的风险也是最大的。
相关性在投资组合领域也非常重要，是分散化投资风险的核心思想。相关性越弱越有利于投资组合的分散化。相关性使用协方差或相关系数来衡量，我们使用DataFrame.cov()函数得到五只股票的协方差，可以看出五只股票的相关性都不是太强，并且五只股票并没有负相关——协方差都为正，一个原因可能是我们只选取了五只股票，而想要有效地分散投资风险，一般需要几十只股票。
表2-2 各股票收益协方差值

df_corr = df.corr()

图2-17 相关系数矩阵
收益率的年化波动率–方差
df_vol = df.std()*np.sqrt(252)

图2-18 收益率年化波动率
2.2.4 模型构建及可视化功能
基于最优夏普比率构建股票投资组合，将总资产按比例投入到不同的股票上。
根据投资组合有效前沿以及资产市场线计算绘图，以此更直观的看到资本市场线与投资组合各数据的关系。
x = np.random.random(5)
weight = x / np.sum(x)
计算随机权重下预期收益率
dfxxport = np.sum(weight*df_m)
投资组合收益率波动率
v_p = np.sqrt(np.dot(weight,np.dot(df_c,weight.T)))

图2-19 收益率波动率运行结果图
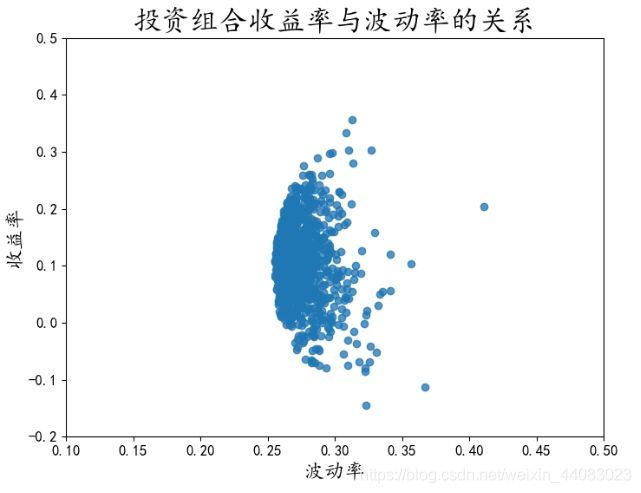
（1）绘制可行集
Rp = [] # 创建股票组合收益率数组
Vp = [] # 创建股票组合收益波动率数组
for i in np.arange(999): # 随机999个不同预期收益率和收益波动率
x = np.random.random(5) #5个一组计算
weight = x/np.sum(x) #和
Rp.append(np.sum(weight*df_m)) #联结数组率写入Rp数组
Vp.append(np.sqrt(np.dot(weight,np.dot(df_c,weight.T))))
#生成散点图
plt.scatter(Vp,Rp,alpha=0.77)

图2-20 投资组合散点图
（2）夏普比率
定义投资五只股票的权重，这里设为每只股票都是0.2
W=np.array([0.2]*5)
df_mean=df.mean()*len(df.index)
df_cov=df.cov()*len(df.index)
投资组合的期望收益
r_df=np.dot(df_mean,W)
var_df=np.dot(W,df_cov)
投资组合的方差
var_df=np.dot(var_df,W.T)
sharp_ratio=r_df/var_df

图2-21 夏普比率
（3）构建有限前沿
构建最优化函数f(w)获得最小波动率：f(w)[1] 假设预期收益率为0.1
C = ({‘type’:‘eq’,‘fun’:lambda x:np.sum(x)-1})
B = tuple((0,1) for x in range(len(df_m)))
(Vmin_f,len(df_m)*[1.0/len(df_m),])
print(round(result[‘x’][i],4))

2-22 预期收益下各股票权重占比值
plt.pie()

图2-23 预期收益下各股票权重占比饼图
（4）资本市场线可视化
Result=sco.minimize(Vmin_f,len(df_m)[1.0/len(df_m),],method=‘SLSQP’,bounds=bnds,constraints=cons)
Rp_vmin = np.sum(df_mresult[‘x’])
Vp_vmin=result[‘fun’]

图2-24 最小预期收益率及波动率数值结果
Rf = 0.02
slope = -result_SR[‘fun’] # 资本市场线斜率
Rm = np.sum(df_m*result_SR[‘x’]) #计算预期收益率
Vm = (Rm-Rf) / slope

图2-25 市场组合预期收益率及波动率数值结果
Rp_cml = np.linspace(0.02,0.6)
Vp_cml = (Rp_cml-Rf) / slope

图2-26 投资组合有效前沿可视化

代码

3.2运行代码
（1）数据采集.Py
import pandas as pd
import tushare as ts
import csv
ts.set_token('bc6edc25e6c0d0938accb6f0cb65130c1c0c1640a3900df5f042c893')#设置token，只需设置一次
pro = ts.pro_api()
#对齐文本#
pd.set_option('display.unicode.ambiguous_as_wide', True)
pd.set_option('display.unicode.east_asian_width', True)
pd.set_option('display.width', 180) # 打印宽度(**重要**)
#查询当前所有正常上市交易的股票列表  茅台600519.SH、美的000333.SZ、京东方
000725SZ、恒瑞医药600276.SH和苏宁易购002024.SZ
data = pro.query('stock_basic', exchange='', list_status='L', fields='ts_code,symbol,name,area,industry,list_date')
data.to_excel('D:\Fun\data\\data.xlsx')
print(data.head())
qdpj = pro.query('daily', ts_code='600600.SH', start_date='20200101', end_date='20210507',fields='trade_date,close')
qdpj.rename(columns={'close':'qdpj','trade_date':'date'}, inplace = True)
meidi=pro.query('daily', ts_code='000333.SZ', start_date='20200101', end_date='20210507',fields='trade_date,close')
meidi.rename(columns={'close':'meidi','trade_date':'date'}, inplace = True)
hksw=pro.query('daily', ts_code='002022.SZ', start_date='20200101', end_date='20210507',fields='trade_date,close')
hksw.rename(columns={'close':'hksw','trade_date':'date'}, inplace = True)
hryy=pro.query('daily', ts_code='600276.SH', start_date='20200101', end_date='20210507',fields='trade_date,close')
hryy.rename(columns={'close':'hryy','trade_date':'date'}, inplace = True)
xpp=pro.query('daily', ts_code='603711.SH', start_date='20200101', end_date='20210507',fields='trade_date,close')
xpp.rename(columns={'close':'xpp','trade_date':'date'}, inplace = True)
#青岛啤酒数据
print(qdpj.head())
alldata = pd.merge(pd.merge(pd.merge(pd.merge(qdpj, meidi,on='date'),xpp,on='date'),hksw,on='date'),hryy,on='date')
#转成中文   alldata.rename(columns={'qdpj':'青岛啤酒','trade_date':'日期','meidi':'美的','hksw':'华科生物','hryy':'恒瑞药业','xpp':'香飘飘'}, inplace = True)
alldata.to_csv('D:\Fun\data\\all.csv')
print(alldata.head())
alldata.rename(columns={'qdpj':'青岛啤酒','meidi':'美的','hksw':'华科生物','hryy':'恒瑞药业','xpp':'香飘飘'}, inplace = True)
alldata.to_csv('D:\Fun\data\\allChinaTitle.csv')



（2）收益数据可视化.py
import pandas as pd
import tushare as ts
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
import datetime
from datetime import datetime
import numpy as np
import scipy.optimize as sco
import csv

# 设置坐标轴的标签与标题
mpl.rcParams["font.family"] = "Kaiti"
mpl.rcParams["axes.unicode_minus"] = False
mpl.rcParams["font.style"] = "normal"
mpl.rcParams["font.size"] = 10

#读入csv文件数据
filename = 'D:\Fun\data\\all.csv'
with open(filename) as f:
    reader = csv.reader(f)
    header_row = next(reader) 
#创建列表
    dates,meidis,qdpjs,xpps,hksws,hryys = [],[],[],[],[],[]
#遍历并存到列表中
    for row in reader:
        current_date = datetime.strptime(row[1], "%Y%m%d")
        dates.append(current_date)
        #!!!!!数据存储到csv中读取数据是字符串形式，将其转换为float或者int型
        qdpj = float(row[2])
        meidi = float(row[3])
        xpp = float(row[4])
        hksw = float(row[5])
        hryy = float(row[6])

        meidis.append(meidi)
        qdpjs.append(qdpj)
        xpps.append(xpp)
        hksws.append(hksw)
        hryys.append(hryy)

#绘图
plt.plot(dates,meidis,label="美的")
plt.plot(dates,qdpjs,label="青岛啤酒")
plt.plot(dates,xpps,label="香飘飘")
plt.plot(dates,hksws,label="华科生物")
plt.plot(dates,hryys,label="恒瑞药业")
plt.legend(loc="best")
plt.title("股票价格历史走势", fontproperties="Kaiti", fontsize=24)  # Kaiti 中文楷体 fontproperties字体
plt.xlabel("日期",fontsize=20)
plt.ylabel("股票价格",fontsize=20)
plt.savefig('D:\Fun\data\\股票价格走势折线图.png')
plt.show()

（3）收益率可视化
df=pd.read_csv('D:/Fun/data/all.csv')
#shift:下移  上移1位：shift（-1）
#计算日收益率
df['Rqdpj'] = np.log(df['qdpj']) - np.log(df['qdpj'].shift(-1))
df['Rmeidi'] = np.log(df['meidi']) - np.log(df['meidi'].shift(-1))
df['Rxpp'] = np.log(df['xpp']) - np.log(df['xpp'].shift(-1))
df['Rhksw'] = np.log(df['hksw']) - np.log(df['hksw'].shift(-1))
df['Rhryy'] = np.log(df['hryy']) - np.log(df['hryy'].shift(-1))
#去空
df.dropna(inplace=True)
df.to_csv('D:\Fun\data\\R.csv')

filename = 'D:\Fun\data\\R.csv'
with open(filename) as f:
    reader = csv.reader(f)
header_row = next(reader) 
    dates,meidis,qdpjs,xpps,hksws,hryys = [],[],[],[],[],[]
    for row in reader:
        current_date = datetime.strptime(row[2], "%Y%m%d")
        dates.append(current_date)
       
        qdpj = float(row[8])
        meidi = float(row[9])
        xpp = float(row[10])
        hksw = float(row[11])
        hryy = float(row[12])

        meidis.append(meidi)
        qdpjs.append(qdpj)
        xpps.append(xpp)
        hksws.append(hksw)
        hryys.append(hryy)

#绘图
plt.figure(figsize=(17,9))
plt.plot(dates,meidis,label="美的")
plt.plot(dates,qdpjs,label="青岛啤酒")
plt.plot(dates,xpps,label="香飘飘")
plt.plot(dates,hksws,label="华科生物")
plt.plot(dates,hryys,label="恒瑞药业")
plt.legend(loc="best")
plt.title("股票日收益率波动情况", fontproperties="Kaiti", fontsize=32)  
plt.xlabel("日期",fontsize=24)
plt.ylabel("日收益率波动范围",fontsize=24)
plt.savefig('D:\Fun\data\\日收益率折线图.png')
plt.show()

#日收益率可视化.py
df=pd.read_csv("D:/Fun/data/R.csv",index_col='date',parse_dates=['date'])[['Rxpp','Rqdpj','Rmeidi','Rhksw','Rhryy']]
df[['Rxpp','Rqdpj','Rmeidi','Rhksw','Rhryy'] ].plot(figsize=(17,9))
plt.legend(["香飘飘", "青岛啤酒",'美的','华科生物','恒瑞药业'])
plt.title("股票日收益率波动情况", fontproperties="Kaiti", fontsize=32)  
plt.xlabel("日期",fontsize=24)
plt.ylabel("日收益率波动范围",fontsize=24)
plt.savefig('D:\Fun\data\\日收益率折线图2.png')
plt.show()
plt_dis=df[['香飘飘','青岛啤酒','美的','华科生物','恒瑞药业'] ].plot(figsize=(17,9),kind="density")
plt_dis.set_title("股票日收益率分布状况", fontproperties="Kaiti", fontsize=32)  
plt_dis.set_xlabel("日期",fontsize=24)
plt_dis.set_ylabel("日收益率密度",fontsize=24)
plt.savefig('D:\Fun\data\\日收益率分布图.png')
plt.show()

#投资优化组合可视化.py
df=pd.read_csv("D:/Fun/data/R.csv",index_col='date',parse_dates=['date'])[['Rxpp','Rqdpj','Rmeidi','Rhksw','Rhryy']]
df.rename(columns={'Rqdpj':'青岛啤酒','Rmeidi':'美的','Rhksw':'华科生物','Rhryy':'恒瑞药业','Rxpp':'香飘飘'}, inplace = True)

df_m=df.mean()*252
df_v=df.var()*252
df_c=df.cov()*252
df_corr = df.corr()
df_vol = df.std()*np.sqrt(252)
x = np.random.random(5)
weight =  x / np.sum(x)
dfxxport = np.sum(weight*df_m)
v_p = np.sqrt(np.dot(weight,np.dot(df_c,weight.T)))

W=np.array([0.2]*5)
df_mean=df.mean()*len(df.index)
df_cov=df.cov()*len(df.index)
r_df=np.dot(df_mean,W) 
print('组合得到的期望收益率',r_df)
var_df=np.dot(W,df_cov)
var_df=np.dot(var_df,W.T)
sharp_ratio=r_df/var_df 
print('夏普比率',sharp_ratio)

# 构建有限前沿
import scipy.optimize as sco
def f(w):  # 构建最优化函数
    w = np.array(w)
    Rp_opt = np.sum(w*df_m)
    Vp_opt = np.sqrt(np.dot(w,np.dot(df_c,w.T)))
    return np.array([Rp_opt,Vp_opt])

def Vmin_f(w):
    return f(w)[1]
cons = ({'type':'eq','fun':lambda x:np.sum(x)-1})
bnds = tuple((0,1) for x in range(len(df_m)))
result=sco.minimize(Vmin_f,len(df_m)*[1.0/len(df_m),],method='SLSQP',bounds=bnds,constraints=cons)
print("投资组合预期收益率 10% 时香飘飘的权重",round(result['x'][0],4))
print("投资组合预期收益率 10% 时青岛啤酒的权重",round(result['x'][1],4))
print("投资组合预期收益率 10% 时美的的权重",round(result['x'][2],4))
print("投资组合预期收益率 10% 时华科生物的权重",round(result['x'][3],4))
print("投资组合预期收益率 10% 时恒瑞药业的权重",round(result['x'][4],4))
plt.pie([round(result['x'][0],4),round(result['x'][1],4),round(result['x'][2],4),round(result['x'][3],4),round(result['x'][4],4)], labels=["香飘飘", "青岛啤酒", "美的", "华科生物", "恒瑞药业"], explode=[0, 0, 0, 0, 0.2])
Rp_vmin = np.sum(df_m*result['x'])
Vp_vmin = result['fun']
print('波动率在可行集是全局最小值的投资组合预期收益率',round(Rp_vmin,4))
print('在可行集是全局最小值的波动率',round(Vp_vmin,4))

#有效前沿的可视化（星号以上部分才是资本市场线）
Rp_target = np.linspace(-0.1,0.6,100)
Vp_target = []
for r in Rp_target:
    conss = ({'type':'eq','fun':lambda x:np.sum(x)-1},{'type':'eq','fun':lambda x:f(x)[0]-r})
    bndss = tuple((0, 1) for x in range(len(df_m)))
    result = sco.minimize(Vmin_f,len(df_m)*[1.0/len(df_m),],method='SLSQP',bounds=bndss,constraints=conss)
Vp_target.append(result['fun'])

def F(w):
    Rf = 0.02
    w = np.array(w)
    Rp_opt = np.sum(w*df_m)
    Vp_opt = np.sqrt(np.dot(w,np.dot(df_c,w.T)))
    SR = (Rp_opt-Rf) / Vp_opt    
    return np.array([Rp_opt,Vp_opt,SR])

def SRmin_F(w):
    return -F(w)[2]

cons_SR = ({'type':'eq','fun':lambda x:np.sum(x)-1})
result_SR = sco.minimize(SRmin_F,len(df_m)*[1.0/len(df_m),],method='SLSQP',bounds=bnds,constraints=cons_SR)

Rf = 0.02
slope = -result_SR['fun'] 
Rm = np.sum(df_m*result_SR['x'])   
Vm = (Rm-Rf) / slope
print('市场组合的预期收益率',round(Rm,4))
print('市场组合的波动率',round(Vm,4))

Rp_cml = np.linspace(0.02,0.6)
Vp_cml = (Rp_cml-Rf) / slope
plt.scatter(Vp,Rp,s=10)
plt.plot(Vp_target,Rp_target,'r-',label=u'有效前沿',lw=2.5)
plt.plot(Vp_cml,Rp_cml,'b--',label=u'资本市场线',lw=2.5)
plt.plot(Vp_vmin,Rp_vmin,'b*',label=u'全局最小波动率',markersize=18)
plt.plot(Vm,Rm,'g*',label=u'市场组合',markersize=14)
plt.xlabel(u'波动率',fontsize=24)
plt.ylabel(u'收益率',fontsize=24)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.xlim(0.15,0.48)
plt.ylim(-0.1,0.45)
plt.title(u'投资组合理论的可视化',fontsize=24)
plt.legend(fontsize=13)
plt.show()