opencv-python 详解霍夫线变换

目录

应用场景：

数学原理：

OpenCV霍夫直线检测基本流程

实验代码请看我的另一篇文章： 

---

应用场景：

        找出二值图中的直线以及测量直线的角度

数学原理：

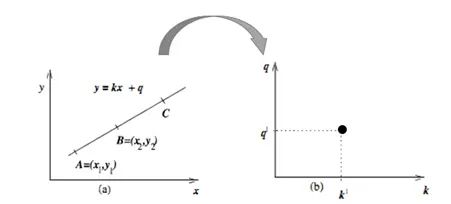
笛卡尔坐标系内，两个点可以确定一条线 y = k*x + q

霍夫空间变换是一种非常简单的变换，其实就是直线方程y=kx+q的另一种写法：

• 图像空间：y=kx+q （变量是y和x）
• 霍夫空间：q=-xk+y（变量是q和k）

变换后的空间成为霍夫空间。即：笛卡尔坐标系中一条直线，对应霍夫空间的一个点。

 反过来同样成立（霍夫空间的一条直线，对应笛卡尔坐标系的一个点）：

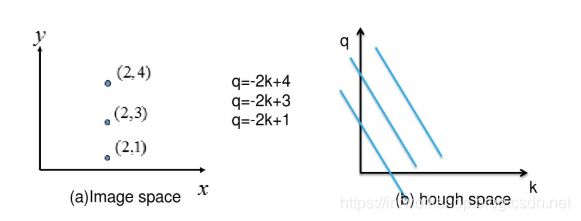
笛卡尔坐标系中两个点对应霍夫空间两条线

如果笛卡尔坐标系三个点共线，对应的霍夫空间的三条线相交于一点

霍夫变换的后处理的基本方式：选择由尽可能多直线汇成的点。 

但是，按照直角坐标系表示的话会出现下图的情况：当图像空间中点共的线垂直于x轴时，斜率无限大，在霍夫空间无法找到交点。因而，人们最终引入了极坐标的表示法。

        极坐标下的霍夫直线检测原理与直角坐标系下完全一致，唯一需要重新推导的是与霍夫空间的极坐标参数函数：

 化简便可得到:

 如果对于一个给定点，意味着每一对代表一条通过点的直线。我们在极坐标对极径极角平面绘出所有通过它的直线, 将得到一条正弦曲线. 例如, 对于给定点X_0= 8 和Y_0= 6 我们可以绘出下图 (在平面):

 极坐标与笛卡尔坐标的转换公式，从极坐标转换 (r,θ) 在笛卡尔坐标系 (x,y) :

x = r × cos( θ )
y = r × sin( θ )

从笛卡儿坐标转换 (x,y) 到极坐标 (r,θ):

r = √(x2+y2)
θ = tan-1 (y/x)

这个值tan-1( y/x ) 可能需要进行调整:

象限I: 使用计算器值
象限II: Add 180°
象限III: Add 180°
象限 IV: Add 360°

在极坐标系下，其实是一样的：极坐标的点→霍夫空间的直线，只不过霍夫空间不再是[k,q]的参数，而是

OpenCV霍夫直线检测基本流程

1. 读取图像，边缘检测+灰度图转换
2. 调用HoughLines()、HoughLinesP()
3. 在图中依次绘制出每条线段

 标准HoughLines()变换 和 概率霍夫线变换HoughLinesP():

cv2.HoughLines()
	dst:  要检测的二值图（一般是阈值分割或边缘检测后的图）
	rho : 参数极径 r 以像素值为单位的分辨率. 我们使用 1 像素，值越大，考虑越多的线
	theta: 参数极角 \theta 以弧度为单位的分辨率. 我们使用 1度 (即CV_PI/180)，值越小，考虑越多的线
	threshold:    设置阈值： 一条直线所需最少的的曲线交点，值越小，考虑越多的线
cv2.HoughLinesP(dst, lines, 1, CV_PI/180, 50, 50, 10 )
	dst:    要检测的二值图（一般是阈值分割或边缘检测后的图） 
	rho :   参数极径 r 以像素值为单位的分辨率. 我们使用 1 像素.
	theta:  参数极角 \theta 以弧度为单位的分辨率. 我们使用 1度 (即CV_PI/180)
	threshold:    设置阈值： 一条直线所需最少的的曲线交点。超过设定阈值才被检测出线段，值越大，基本上意味着检出的线段越长，检出的线段个数越少。
	minLinLength: 能组成一条直线的最少点的数量. 点数量不足的直线将被抛弃.
	maxLineGap:   能被认为在一条直线上的两点的最大距离。
        return:返回的是含有一条直线的起始点和终点坐标[x1,y1,x2,y2]

        标准霍夫变换，其本质上就是把图像中的边缘像素映射到它的霍夫空间，比如一共有M个边缘像素，则所有的边缘像素都需要进行映射，其运算量和所需内存都会很大。如果只处理图像的m（m

实验代码请看我的另一篇文章： 

https://blog.csdn.net/RayChiu757374816/article/details/119648808?spm=1001.2014.3001.5501