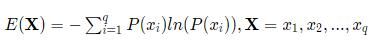【AI Studio】飞桨图像分类零基础训练营 - 02 - 图像分类基础概念
前言: 第二节课,老师讲解了4个简单神经网络,循序渐进,思路清晰。不过这个是基于我本身就对深度学习有一定概念认知的基础上,如果是第一次听可能一头雾水
(直播时就有人吵,同为小白的我都感到丢脸)。第二次看详细的paddle网络代码讲解,第一次是七日图像分割。现在已经对paddle框架有了认知了,之后的进度应该会顺利一点。
- 我忘记了很多神经网络的细节,在写第二次作业时才发现这个问题。然后我发现以下的笔记很多都在胡扯,只有最后的总结和复制老师的程序能参考一下。在此提前说一下。
目录
- 【AI Studio】飞桨图像分类零基础训练营 - 02 - 图像分类基础概念
-
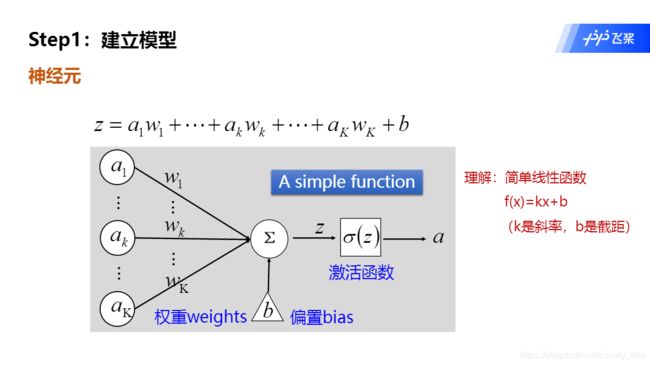
- 一、线性回归模型
-
- ① 第一步,处理数据
- ②第二步,构建线性回归模型
- ③第三步,构建优化器和损失函数
- ④第四步,开始训练
- 二、SoftMax分类器
-
- 1.概念:信息量
- 2.概念:信息熵
- 3.概念:交叉熵
- 4.实战:手写体数字识别
- 三、构建多层感知机模型
- 四、构建卷积网络模型LeNet-5
-
- 1.构建LeNet-5模型进行MNIST手写数字分类
- 2.构建LeNet-5模型进行CIFAR10图像分类
- 五、总结
- 六、作业
-
- 1.问题,激活函数Relu
- 2.实践,测试激活函数
———————————————
【AI Studio】飞桨图像分类零基础训练营 - 02 - 图像分类基础概念
课程文档:
https://aistudio.baidu.com/aistudio/education/preview/1106964
项目合集
https://aistudio.baidu.com/aistudio/projectdetail/1354419
一、线性回归模型
基于PaddlePaddle2.0-构建线性回归模型
https://aistudio.baidu.com/aistudio/projectdetail/1322247
【目录】【中文】【deplearning.ai】【吴恩达课后作业目录】
https://blog.csdn.net/u013733326/article/details/79827273
- 还有一些其他学习者发布的笔记,我觉得都能很好的促进理解。当时单单看吴恩达的教程并不能完全理解,是这篇笔记救了我。
其他学习者的笔记:神经网络(深度学习)从入门到精通(放弃)
https://blog.csdn.net/u014162133/article/details/81181194
因为个人已经入门很多次了,我直接上代码给已经有概念的人复习一遍,没有概念的请把推荐笔记看一遍先。我本来是这么认为的,结果在写第二次作业时发现其实自己很多都忘却了。然后我发现以下的笔记很多都在胡扯,只有最后的总结和复制老师的程序能参考一下。
① 第一步,处理数据
import numpy
num_inputs=2 # 定义输入参数数量
num_examples=500 # 定义训练次数
true_w=[1.2,2.5] # 定义需要生成数据的参数,也是模型训练的最终目标w
true_b=6.8 # 定义需要生成数据的参数,也是模型训练的最终目标b
# 随机生成x
features = numpy.random.normal(0,1,(num_examples, num_inputs)).astype('float32')
# 利用随机生成的x,生成y
labels = features[:,0]*true_w[0]+features[:,1]*true_w[1]+true_b
# 增加不确定变量叠加在y上,很小的一个偏置(如果不增加,几个式子就可以解方程得出答案)
labels = labels + numpy.random.normal(0,0.001,labels.shape[0])
# 转换数组的数据类型
labels = labels.astype('float32')
#注意:需要在最后增加一个维度 嗯嗯嗯,这个操作大概是为paddle框架用的。
labels = numpy.expand_dims(labels,axis=-1)
②第二步,构建线性回归模型
- 在开课前的预习里,就有学习了paddle的
Tensor数据类型,至关重要的基础知识。“Tensor是类似于 Numpy array 的概念。” - 另一个概念!
paddle.nn.Linear()等函数的运用,这是飞桨框架的核心特点 —— 一句定义一层。
飞桨开发指南-一文带你了解飞桨静态图运行机制
https://aistudio.baidu.com/aistudio/projectdetail/462062?qq-pf-to=pcqq.group
import paddle
# 将普通的Numpy转换为Paddle框架能用的Tensor类型
train_data=paddle.to_tensor(features)
# 上一行是转换输入数据,下一行是转换输出数据
y_true=paddle.to_tensor(labels)
# 定义一层网络,输入2,输出1。
model=paddle.nn.Linear(in_features=2, out_features=1)
③第三步,构建优化器和损失函数
- 在飞桨框架的帮助下,最麻烦的损失计算,梯度下降直接一句话搞定了(初学者莫多想,它就是一句话搞定了)。然后直接返回一个损失值。
# 实现随机梯度下降算法的优化器
sgd_optimizer=paddle.optimizer.SGD(learning_rate=0.001, parameters=model.parameters())
# 计算预测值和目标值的均方差误差。
mse_loss=paddle.nn.MSELoss()
④第四步,开始训练
- 这个模型过于简单,有些操作被省略了。看懂后,趁热打铁进入下一节。
for i in range(5000):
# 记住这种函数操作,把 输入 丢进 模型 中就可以
y_predict = model(train_data)
# 返回的值就是出,输出再和准确值计算差值
loss=mse_loss(y_predict, y_true)
# 然后“问号?”三连,
loss.backward()
sgd_optimizer.step()
sgd_optimizer.clear_grad()
# 就成功了……
print(model.weight.numpy())
[[1.2000061] [2.5001166]]
print(model.bias.numpy())
[6.799932]
print(loss.numpy())
[1.09125e-06]
- 提一点,
loss是损失函数的值,acc是准确率的意思。 - 经过5000次迭代优化,模型参数估计值为1.2、2.5,截距项估计值为6.8。这与我们事前设定的模型参数是一致的,这表明机器已经从样本数据中学习到了真实参数。
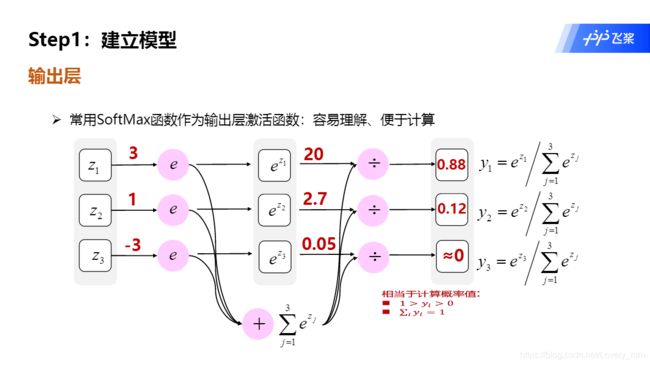
二、SoftMax分类器
基于PaddlePaddle2.0-构建SoftMax分类器
https://aistudio.baidu.com/aistudio/projectdetail/1323298
SoftMax分类器是根据输入特征来对离散型输出概率做出预测的模型,适用于多分类预测问题。 我们以手写数字分类为例构建一个分类器,根据手写数字的光学识别图片来预测这张图片所包含的数字。
- 其实这属于一个激活函数,它把一些输入映射为0-1之间的实数,并且归一化保证和为1,因此多分类的概率之和也刚好为1。
小白都能看懂的softmax详解
https://blog.csdn.net/bitcarmanlee/article/details/82320853
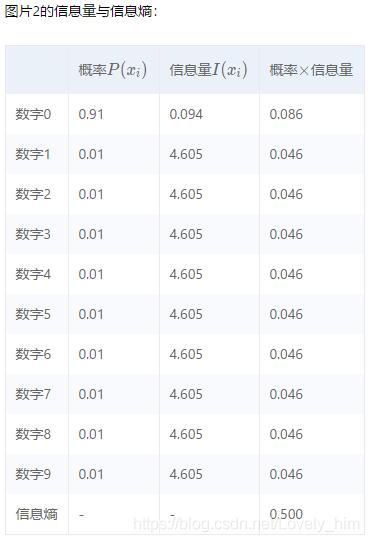
1.概念:信息量
信息论创始人Shannon在“通讯的数学理论”一文中指出“信息是用来消除随机不确定性的东西”。信息量衡量的是某个具体事件发生所带来的信息,信息量大小就是这个信息消除不确定性的程度。
设某个信息发生的概率为P(x),其信息量表示为:
- 简单理解,就是把概率P带入公式-ln§ 得到的就是信息量 i
2.概念:信息熵
信息熵是所有可能发生事件所带来的信息量的期望。信息熵越大,代表事物越具不确定性。设X是一个离散型随机变量,类别个数为q,信息熵表示为:
3.概念:交叉熵
- 我们先设定判定标准:交叉熵的值越小,模型预测效果就越好。
(刚刚发现这个函数之前在吴恩达学过,我居然忘光了) - 这个公式概念很巧妙的,当预测与实际接近时,就会小,反之则大。这个特性可以用于做损失函数,然后就有了“经典损失函数——交叉熵损失函数”。
经典损失函数:交叉熵(附tensorflow)
https://blog.csdn.net/weixin_37567451/article/details/80895309
4.实战:手写体数字识别
手写数字分类数据集来源MNIST数据集,该数据集可以公开免费获取。该数据集中的训练集样本数量为60000个,测试集样本数量为10000个。每个样本均是由28×28像素组成的矩阵,每个像素点的值是标量,取值范围在0至255之间。我们使用
paddle.vision.datasets.MNIST()方法来下载和加载MNIST数据集。
- 注意注意!在实际的代码实现过程中:线性模型+交叉熵损失函数,即softmax分类器。
import paddle
# 加载数据
train_dataset=paddle.vision.datasets.MNIST(mode="train", backend="cv2") #训练数据集
test_dataset=paddle.vision.datasets.MNIST(mode="test", backend="cv2") #测试数据集
# 设定模型,记住“paddle.nn.Sequential”这个方法,可以打包复数层网络。
linear=paddle.nn.Sequential(
paddle.nn.Flatten(),#将[1,28,28]形状的图片数据改变形状为[1,784]
paddle.nn.Linear(784,10)
)
# 利用paddlepaddle2的高阶功能,可以大幅减少训练和测试的代码量
# 把模型丢入Model
model=paddle.Model(linear)
# 下面是高阶API的用法,提前了解一下。其实就是打包了几个操作,更加方便了。
model.prepare(paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters()),
paddle.nn.CrossEntropyLoss(), #交叉熵损失函数。线性模型+该损失函数,即softmax分类器。
paddle.metric.Accuracy(topk=(1,2)))
model.fit(train_dataset, epochs=2, batch_size=64, verbose=1)
model.evaluate(test_dataset,batch_size=64,verbose=1)
三、构建多层感知机模型
基于PaddlePaddle2.0-构建多层感知机模型
https://aistudio.baidu.com/aistudio/projectdetail/1323886
线性回归模型和SoftMax分类器都属于单层全连接神经网络,下面介绍一种具有多层结构的全连接神经网络——多层感知机。多层感知机是一种至少具有1个隐藏层的全连接神经网络,每个隐藏层输出需要经过激活函数转换。
如果是多分类问题,可以把经过激励函数转化后的值进行SoftMax运算,输出得到样本在各类别上的概率。
-
这个介绍多层神经网络,也就是含隐藏层的操作。其他东西都一样,直接上代码。
-
大部分都一样,不过有点需要特别说明。多层网络就开始使用:定义一个模型类,初始化内定义各层网络的配置;然后其中的方法“
forward()”就是用设定的各层网络,前后搭配组合在一起,形成模型。 -
还有一点要注意,线性网络中,每次隐藏层输出都要接一个激活层。不要忘记了
import paddle
import paddle.nn.functional as F
from paddle.vision.transforms import ToTensor
#导入数据
train_dataset=paddle.vision.datasets.MNIST(mode="train", transform=ToTensor())
val_dataset=paddle.vision.datasets.MNIST(mode="test", transform=ToTensor())
#定义模型
class MLPModel(paddle.nn.Layer):
def __init__(self):
super(MLPModel, self).__init__()
self.flatten=paddle.nn.Flatten()
self.hidden=paddle.nn.Linear(in_features=784,out_features=128)
self.output=paddle.nn.Linear(in_features=128,out_features=10)
# 注意,多层网络就开始引入forward函数概念了。
def forward(self, x):
x=self.flatten(x)
x=self.hidden(x) #经过隐藏层
x=F.relu(x) #经过激活层,先经过激活函数再到输出10分类
x=self.output(x)
return x
model=paddle.Model(MLPModel())
# 利用paddlepaddle2的高阶功能,可以大幅减少训练和测试的代码量
model.prepare(paddle.optimizer.Adam(parameters=model.parameters()),
paddle.nn.CrossEntropyLoss(),
paddle.metric.Accuracy())
model.fit(train_dataset,
epochs=5,
batch_size=64,
verbose=1)
model.evaluate(val_dataset,verbose=1)
四、构建卷积网络模型LeNet-5
基于PaddlePaddle2.0-构建卷积网络模型LeNet-5
https://aistudio.baidu.com/aistudio/projectdetail/1329509
LeNet-5是卷积神经网络模型的早期代表,它由LeCun在1998年提出。该模型采用顺序结构,主要包括7层(2个卷积层、2个池化层和3个全连接层),卷积层和池化层交替排列。
- 各层的内容我就不复制粘贴了,简单点说明就是:卷积
conv+池化pool+线性+……叠加循环之类的。(第二节课老师举例说明和简单介绍,第三课才细讲了一下卷积。我也放到下一课笔记再写。) - 记住卷积和池化的2个单词,之前看图像分割的教程,一开始大半听不懂……
- 池化
pool操作也可以理解为和下采样一个意思,再大白话一点就是理解成缩小图片,放大图片就是上采样。 - 重点!:下采样的目的是:增加增大感受野(视野的野)。因为原本几个像素点的内容都合成一个像素点内了。
1.构建LeNet-5模型进行MNIST手写数字分类
又臭又长的代码来 ,老师写得很工整明,太爱了。
import paddle
import paddle.nn.functional as F
from paddle.vision.transforms import Compose, Normalize
transform = Compose([Normalize(mean=[127.5],
std=[127.5],
data_format='CHW')])
#导入MNIST数据
train_dataset=paddle.vision.datasets.MNIST(mode="train", transform=transform)
val_dataset=paddle.vision.datasets.MNIST(mode="test", transform=transform)
#定义模型
class LeNetModel(paddle.nn.Layer):
def __init__(self):
super(LeNetModel, self).__init__()
# 创建卷积和池化层块,每个卷积层后面接着2x2的池化层
#卷积层L1
self.conv1 = paddle.nn.Conv2D(in_channels=1,
out_channels=6,
kernel_size=5,
stride=1)
#池化层L2
self.pool1 = paddle.nn.MaxPool2D(kernel_size=2,
stride=2)
#卷积层L3
self.conv2 = paddle.nn.Conv2D(in_channels=6,
out_channels=16,
kernel_size=5,
stride=1)
#池化层L4
self.pool2 = paddle.nn.MaxPool2D(kernel_size=2,
stride=2)
#线性层L5
self.fc1=paddle.nn.Linear(256,120)
#线性层L6
self.fc2=paddle.nn.Linear(120,84)
#线性层L7
self.fc3=paddle.nn.Linear(84,10)
#正向传播过程
def forward(self, x):
x = self.conv1(x)
x = F.relu(x)
x = self.pool1(x)
x = F.relu(x)
x = self.conv2(x)
x = self.pool2(x)
x = paddle.flatten(x, start_axis=1,stop_axis=-1)
x = self.fc1(x)
x = F.relu(x)
x = self.fc2(x)
x = F.relu(x)
out = self.fc3(x)
return out
model=paddle.Model(LeNetModel())
model.prepare(paddle.optimizer.Adam(parameters=model.parameters()),
paddle.nn.CrossEntropyLoss(),
paddle.metric.Accuracy())
model.fit(train_dataset,
epochs=5,
batch_size=64,
verbose=1)
model.evaluate(val_dataset,verbose=1)
2.构建LeNet-5模型进行CIFAR10图像分类
- 第一节课有介绍这几个数据集,这些数据集都是在paddle内置的。方便学习和验证模型。
CIFAR10数据集的特点是,比手写数据集分类更多。 - 这一部分是为了证明,单单使用
LeNet-5模型,在处理少分类少数据时才有高准确度。当分类数、图像通道数(彩色图片三通道)时精确度就很低。具体解决方法放到下一课再细讲。 (代码部分就不列了,差不多一样的)
五、总结
- 至于为什么用卷积不用线性网络,因为线性网络参数太多了。图片一大,成百上千的像素点。如果全部像素点都线性全连接网络,那……而卷积的参数数目就少得多,卷积核长乘宽就可以了。
- 更多细节内容待到下一课笔记再说。
六、作业
- 作业题目是构建一个多层感知器,程序的数据处理与模型训练,还有模型测试都已经写好了。我只需要完成模型构建的填空即可。以下是题目:
以下的代码判断就是定义一个简单的多层感知器,一共有三层,两个大小为100的隐层和一个大小为10的输出层,因为MNIST数据集是手写0到9的灰度图像,类别有10个,所以最后的输出大小是10。最后输出层的激活函数是
Softmax,所以最后的输出层相当于一个分类器。加上一个输入层的话,多层感知器的结构是:输入层–>>隐层–>>隐层–>>输出层。
1.问题,激活函数Relu
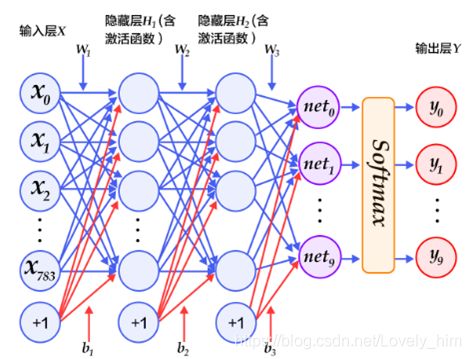
只有自己动手写才发现自己理解有问题,前面听课听的头头是道。- 根据图片表示:线性隐藏层H1和H2,H1好理解,输入784输出100经过relu激活得到100,再把100输入到H2。
- 问题是:隐藏层H2,输入100,输出10,那这个10还需要经过relu激活输出10吗?还是H2输出10后就结束正向传播了?
# 基于PaddlePaddle2.0-构建卷积网络模型LeNet-5 的节选
x = self.fc1(x)
x = F.relu(x)
x = self.fc2(x)
x = F.relu(x)
out = self.fc3(x)
return out
# 基于PaddlePaddle2.0-构建多层感知机模型 的节选
x=self.flatten(x)
x=self.hidden(x) #经过隐藏层
x=F.relu(x) #经过激活层
x=self.output(x)
return x
# 基于PaddlePaddle2.0-构建SoftMax分类器 的节选
linear=paddle.nn.Sequential(
paddle.nn.Flatten(),#将[1,28,28]形状的图片数据改变形状为[1,784]
paddle.nn.Linear(784,10)# 线性模型+交叉熵损失函数,即softmax分类器。
)
- 模仿老师的例子写程序时,发现最好的线性层输出10后就直接返回了,结束正向传播。开始反向传播,和交叉熵损失函数搭配组成softmax分类器。
- 但是作业题目的图片中写着“隐藏层H2(含激活函数)”时,引发的思考,这个H2的激活函数要写在哪里?老师写的例子中有写吗,按我之前的理解应该是有的才对,我一直以为
paddle.nn.Linear的返回值就含激活层操作了,现在发现好像不是。
def forward(self, x):
#请在这里补全传播过程的代码
x = self.x_input(x) # 把图像拍成一维
x = self.LH_1(x) # 输入784个x,计算输出100个y
x = F.relu(x) # 输入100个y,计算100个y'
y = self.LH_2(x) # 再把100个y'当x输入,计算输出新的10个y
# y = F.relu(y) # 根据作业图片要求,事实证明不用,用了整个模型就崩掉了……
return y
2.实践,测试激活函数
- 经过助教的指点,我明白了加入激活函数是为了给多层线性网络加入非线性变化,不然无论多少层都会拍扁对于单层。同时激活函数有很多,下节笔记细讲。
- 我也明白了
SoftMax分类器、SoftMax激活函数的用以,一开始我居然跳过了这个知识点,现在上面的笔记已经补充了。
助教说:paddle.nn.CrossEntropyLoss()中是把交叉熵损失函数和softmax一起合并在一起了,所以不要再加softmax了。你最后一层可以用relu也可以用softmax,都可以,就是训练效果的差距。
- 但我实践发现,对于
MNIST手写数字数据集来说,我最后加和不加激活函数(softmax或Relu),准确率都很高,可能是数据集太简单的缘故。但是,预测结果输出却有很明显的差别,只有加了softmax后输出结果才在0到1之间的概率,而且结果明显。 - 但是助教却说这相当于用了2次
softmax。这也说明了为什么我在老师的项目例子里没有看到softmax激活函数,因为包含在了损失函数中。 - 而我如果加relu,最后就相当于有2个激活函数叠加在一起了,然后预测结果会有很多零。
print(result[0][0])
# [[ -2.661826 -3.217544 1.4394473 3.3448048 -11.59877
# -4.011869 -12.629112 10.715195 0.16913329 0.5076793 ]] # 没加softmax的线性
# [[5.6143895e-10 1.9332323e-18 1.1747437e-09 1.0818614e-09 4.8145010e-15
# 3.0116232e-09 1.4993277e-17 1.0000000e+00 1.2124682e-10 4.7770667e-09]] # 加softmax的线性
# [[-2.0730288 3.2187026 4.494609 0.716204 1.0953971 -3.124497
# -9.232485 17.074171 -1.4758562 2.4306192]] # 没加softmax的卷积
# [[9.1836060e-20 1.5012904e-25 8.1553386e-19 4.0469723e-21 1.6038109e-28
# 1.8038185e-28 1.6038109e-28 1.0000000e+00 6.5071873e-27 6.9125941e-24]] # 加softmax的卷积
# [[ 0. 0. 0. 3.1087685 0. 0.
# 0. 10.235452 0. 0.3576991]] # 加relu的线性