第1章 电路元件和电路定律
文章目录
- 本章重点
- 1. 电路元件
-
- 1.1 电路及集总电路模型
-
- 1.1.1 电路的基本功能
- 1.1.2 集总电路模型
- 1.2 电路变量 电流电压及功率
-
- 1.2.1 电流
- 1.2.2 电压
-
- 题目1:电压、电位、参考点
- 1.2.3 电压和电流的关联参考方向
- 1.2.4 能量和功率
-
- 题目2:参考方向与吸收功率
- 1.3 电阻元件
-
- 1.3.1 线性电阻
- 1.3.2 欧姆定律
- 1.4 电源元件
-
- 1.4.1 理想电压源
- 1.4.2 理想电流源
- 2. 电路定律
-
- 1.5 基尔霍夫定律
-
- 1.5.1 基尔霍夫电流定律(KCL)
-
- 题目3:基尔霍夫电流定律计算支路电流
- 1.5.2 基尔霍夫电压定律(KVL)
-
- 题目4:基尔霍夫电压定律计算支路电压
- 1.6 电阻电路的等效变换
-
- 1.6.1 二端电路
- 1.6.1 电阻的串联
-
- 题目5:串联分压
- 1.6.2 电阻的并联
- 1.6.3 电阻的串并联
-
- 题目5:电阻的串并联等效
- 1.7 电压源的串联和并联
-
- 1.7.1 电压源的串联
- 1.7.2 电压源的并联
- 1.7.3 电压源与支路的串、并联等效
- 1.8 电流源的串联和并联
-
- 1.8.1 电流源的并联
- 1.8.2 电流源的串联
- 1.8.3 电流源与支路的串、并联等效
- 1.9 实际电源与两种电源模型的等效变换
-
- 1.9.1 电压源模型
- 1.9.2 电流源模型
- 1.9.3 两种电源模型的等效变换
-
- 题目6:两种电源之间的转换
本章重点
- 电压、电流的参考方向
- 电路元件特性
- 基尔霍夫定律
1. 电路元件
1.1 电路及集总电路模型
1.1.1 电路的基本功能
(1)实现电能的产生、传输、分配和转换
(2)实现电信号的产生、传输、变换和处理
1.1.2 集总电路模型
1、定义:当实际电路的尺寸远小于最高工作频率所对应的波长时,用几种集总参数元件构成实际器件的模型
集总参数元件(理想元件):
将实际电路理想化,突出其主要电磁性质,忽略次要因素。
2、5种基本的集总电路元件:
电阻元件:消耗电能的元件
电容元件:存储电场能量的元件
电感元件:产生磁场,存储磁场能量的元件
电压源和电流源:将其他形式能量转变为电能
3、5种基本集总电路元件的三个特征:
- 只有两个端子
- 可以把电压或电流按数学方式描述
- 不能分解为其他元件
1.2 电路变量 电流电压及功率
1.2.1 电流
1、定义:
电荷(-)有规则的定向运动
电流方向:
正电荷的运动方向(电荷运动的相反方向)
大小:
单位时间内通过导体横截面的电荷量
i ( t ) = d q ( t ) d t i(t)=\frac{dq(t)}{dt} i(t)=dtdq(t)
1 K A = 1 0 3 A = 1 0 6 m A = 1 0 9 u A 1KA=10^3A=10^6mA=10^9uA 1KA=103A=106mA=109uA
2、假设正方向(参考方向)
① 在解题前设定参考方向(+方向)
② 根据计算结果确定实际方向
若计算结果>0,实际方向与参考方向相同
若计算结果<0,实际方向与参考方向相反
1.2.2 电压
1、定义:
a,b两点间的电压等于单位正电荷从a移至b时所获得或失去的能量
u ( t ) = d w ( t ) d q ( t ) u(t)=\frac{dw(t)}{dq(t)} u(t)=dq(t)dw(t)
1 k V = 1 0 3 V = 1 0 6 m V = 1 0 9 μ V 1kV=10^3V=10^6mV=10^9\mu V 1kV=103V=106mV=109μV
电位:
选定点o为参考点,规定电压 u o u_o uo为0,则a与o之间的电压作为a的电位
大小:
u a b = u a − u b = W a b q u_{ab}=u_a - u_b=\frac{W_{ab}}{q} uab=ua−ub=qWab
方向:
实际方向:电位降低的方向
U a b > 0 , u a > u b , W a b > 0 , 正 电 荷 失 去 能 量 U_{ab}>0,u_a>u_b,W_{ab}>0,正电荷失去能量 Uab>0,ua>ub,Wab>0,正电荷失去能量
参考方向:规定的电压方向
若计算结果u>0,实际方向与参考方向相同
若计算结果u<0,实际方向与参考方向相反

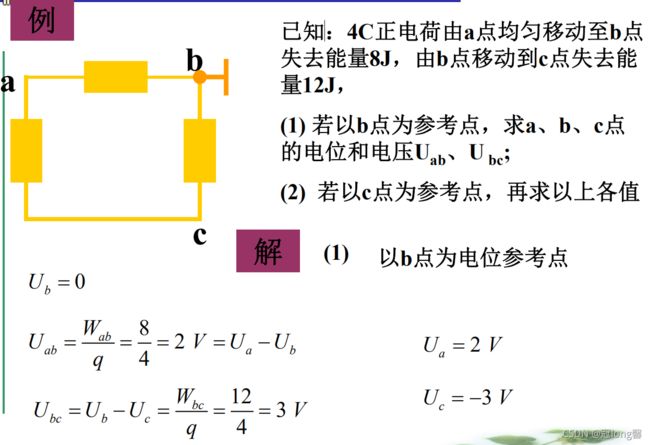
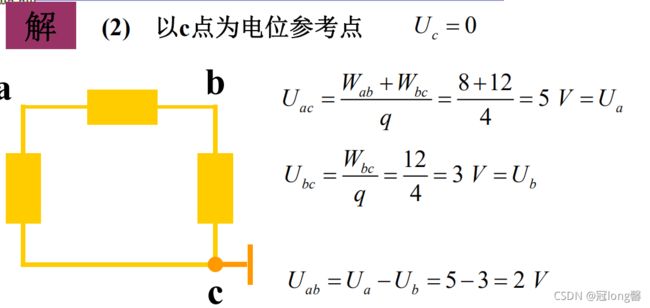
题目1:电压、电位、参考点
(1)参考点一经选定,电路中各点的电位值就是唯一的;
(2)当选择不同的电位参考点时,电路中各点电位值将改变,但任意两点间电压保持不变。
1.2.3 电压和电流的关联参考方向
关联参考方向:电流、电压所选的参考方向一致
1.2.4 能量和功率
1、定义
电功率:
单位时间内元件吸收/提供的能量
大小:
(1)电压与电流取关联参考方向时,元件的吸收功率为:
p = d w d t , u = d w d q , i = d q d t p=\frac{dw}{dt},u=\frac{dw}{dq},i=\frac{dq}{dt} p=dtdw,u=dqdw,i=dtdq
p = U I p=UI p=UI
(2)电压与电流取非关联参考方向时,元件的吸收功率为:
p = − U I p=-UI p=−UI
若P>0,吸收功率或消耗功率(负载作用)
若P<0,输出功率(电源作用,电源的功率可能为+,也可能为-)
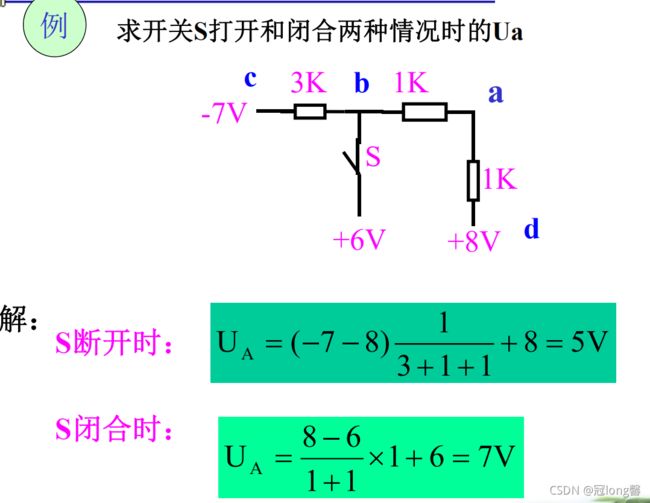
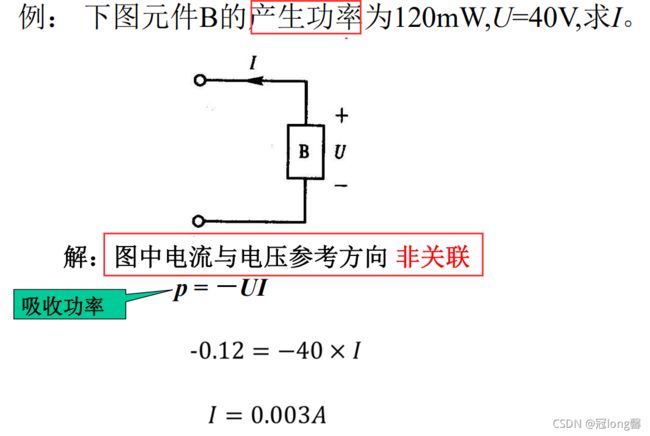
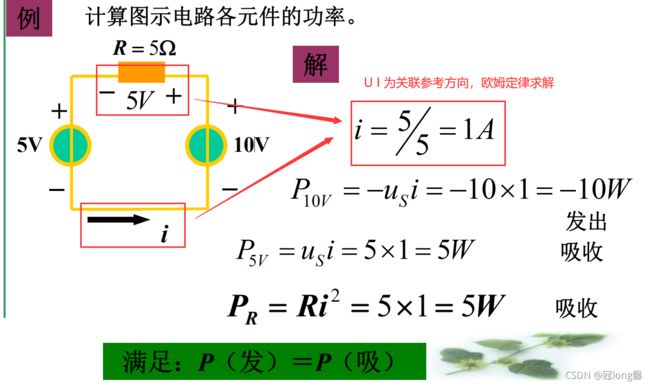
题目2:参考方向与吸收功率
步骤:
① 确定电流与电压的参考方向是否关联
② 吸收功率 or 产生功率
1.3 电阻元件
1.3.1 线性电阻
线性元件:
电阻伏安关系曲线是通过原点的直线
其他:
非线性电阻:电阻伏安关系曲线不是直线
非时变电阻:伏安曲线不随时间变化
时变电阻:伏安曲线随时间变化
1.3.2 欧姆定律
1、定义:
设电阻元件上电流电压为关联参考方向
u ( t ) = R i ( t ) u_{(t)}=Ri_{(t)} u(t)=Ri(t)
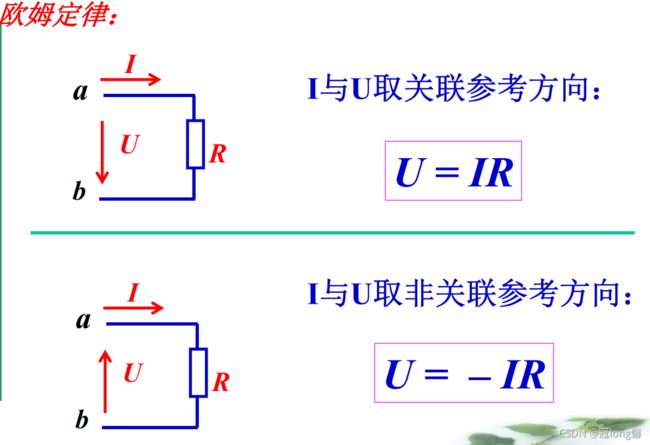
1 k Ω = 1 0 3 Ω = = 1 0 6 m Ω = 1 0 9 μ Ω 1k\Omega=10^3\Omega==10^6m\Omega=10^9\mu\Omega 1kΩ=103Ω==106mΩ=109μΩ
西门子:
G = 1 R G = \frac{1}{R} G=R1
i t = u R = G u i_{t}=\frac{u}{R}=Gu it=Ru=Gu
电阻的开路与短路:
(1)开路:
R = ∞ , G = 0 , i = 0 , U ≠ 0 R=\infty,G=0,i=0,U\neq0 R=∞,G=0,i=0,U=0
(2)短路
R = 0 , G = ∞ , i ≠ 0 , U = 0 R=0,G=\infty,i\neq0,U=0 R=0,G=∞,i=0,U=0
电阻的吸收功率:
电阻元件在任何时刻总是吸收(消耗)功率的。
p = ± U I = u 2 R = i 2 R p=\pm UI=\frac{u^2}{R}=i^2R p=±UI=Ru2=i2R
1.4 电源元件
1.4.1 理想电压源
1.定义
两端电压总能保持定值或一定的时间函数,与流过它的电流I无关的元件
3.理想电压源电压、电流的关系:
① 电源两端电压由电源本身决定,与外电路无关;与流经它的电流的方向、大小无关
② 通过电压源的电流由电源及外电路共同决定
理解: i = u s R i=\frac{u_s}{R} i=Rus,理想电压源不能直接外接导线即电压源不能短路
4. 电压源的功率:
电压源可以对外电路提供电能,真正起电源作用;也可以作为其它电源的负载从外电路吸收能量。
p = ± U I p = \pm UI p=±UI
1.4.2 理想电流源
1.定义:
输出电流总保持定值或一定的时间函数,与它的两端电压u无关的元件
2.理想电流源电压、电流的关系
① 电流源的输出电流由电源本身决定,与外电路无关;与两端电压大小、方向无关
② 电流源两端的电压由电源及外电路共同决定
理解: u = R i s u=Ri_s u=Ris,R不能为inf即电流源不能开路
3.电流源的功率
P = ± U I P=\pm UI P=±UI
2. 电路定律
1.5 基尔霍夫定律
基尔霍夫定律包括基尔霍夫电流定律(KCL)和基尔霍夫电压定律( KVL )。它反映了电路中所有支路电压和电流所遵循的基本规律,是分析集总参数电路的基本定律。基尔霍夫定律与元件特性构成了电路分析的基础。
1.概念:
支路: 电路中通过同一电流的分支
节点:三条以上支路的连接点
路径: 两节点间的一条通路。由支路构成
回路: 由支路组成的闭合路径。
网孔: 内部不含任何支路的回路(特殊的回路)
其中,网孔是回路而回路不一定是网孔
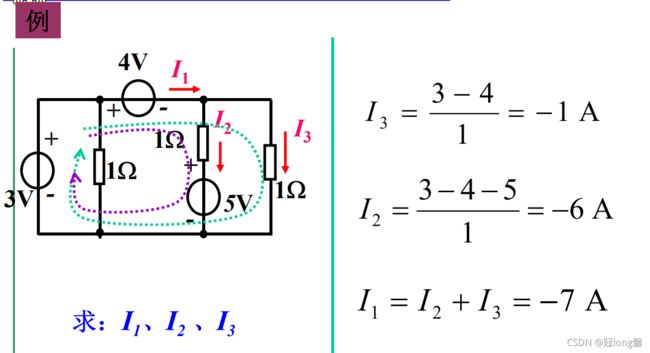
1.5.1 基尔霍夫电流定律(KCL)
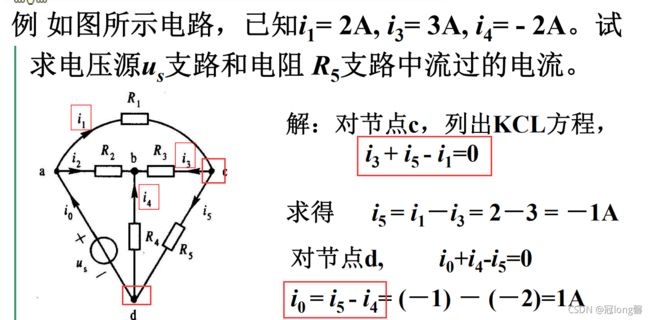
1. 定义:
在集总参考电路中,任意时刻,对任意节点流出或流入该节点电流的代数和为0
∑ b = 1 m i ( t ) = 0 \sum_{b=1}^{m}i(t)=0 b=1∑mi(t)=0
∑ i i n = ∑ i o u t \sum i_{in} = \sum i_{out} ∑iin=∑iout
2. 推广
① KCL可推广应用于电路中包围多个节点的任一闭合面
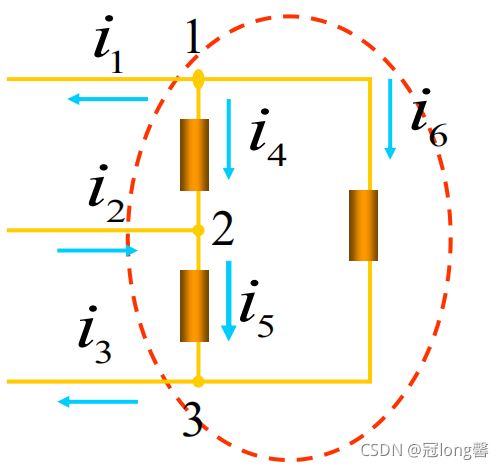
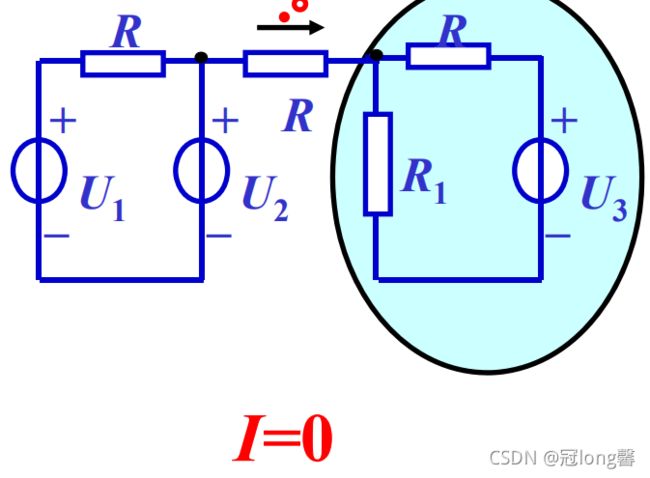
② 两部分电路之间,如果只有一条支路相连接,则该支路上的电流必为零。
题目3:基尔霍夫电流定律计算支路电流
1.5.2 基尔霍夫电压定律(KVL)
1. 定义:
对于电路中的任一回路,按任意方向绕行一周,各部分电压代数和为0
∑ U = 0 \sum U=0 ∑U=0
其中,与绕行方向一致的电压为正,否则取负。
题目4:基尔霍夫电压定律计算支路电压
步骤:
(1) 设定各支路电压的参考方向,指定回路的绕行方向。
2) 按绕行方向沿回路一周,当支路电压的参考方向与回路的绕行方向一致时,该支路电压前面取“+”号;相反时,取“-”号。
1.6 电阻电路的等效变换
电阻电路: 仅由电源和线性电阻构成的电路
分析方法:
①欧姆定律和基尔霍夫定律是分析电阻电路的依据;
②等效变换的方法,也称化简的方法。
1.6.1 二端电路
1. 定义:
任何一个复杂的电路,向外引出两个端钮,且从一个端子流入的电流等于从另一个端子流出的电流。
2. 二端电路等效的概念:
两个二端电路,端口具有相同的电压、电流关系,则等效
u = f ( i ) 与 u ′ = f ( i ′ ) 相 同 u=f(i)与u'=f(i')相同 u=f(i)与u′=f(i′)相同
理解:
① 两电路等效是指在其端口处,对任一同一外电路而言,有同样的电路效果
理解:等效是相对与外电路而言的,而两个对象的内部属性并不相同
1.6.1 电阻的串联
1. 电路特点:
① 总电压等于串联电阻的电压之和(KVL)
② 各电阻顺序连接,流过同一电流 (KCL)
2. 等效电阻:
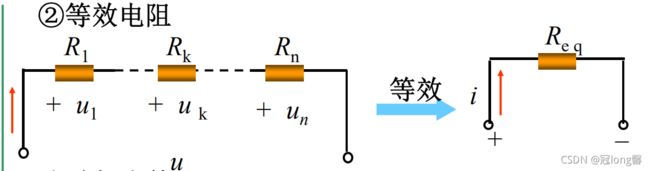
① 电阻: 总电阻等于个电阻之和
R = R 1 + R 2 + … R k R=R_1+R_2+\dots R_k R=R1+R2+…Rk
② 电压: 总电压等于分电压之和
u = R 1 i + R 2 i + … R k i , u k = R k R u u=R_1i+R_2i+\dots R_ki,u_k=\frac{R_k}{R}u u=R1i+R2i+…Rki,uk=RRku
③ 功率: 总功率等于各串联电阻消耗功率的总和,各电阻消耗的功率与电阻大小成正比
p = p 1 + p 2 + ⋯ + p k , p k = i 2 × R k p = p_1+p_2+\dots+p_k,p_k=i^2 \times R_k p=p1+p2+⋯+pk,pk=i2×Rk
3. 串联电阻分压:
① 电压与电阻成正比,因此串联电阻电路可作分压电路
u k = R k R e q × u < u u_k=\frac{R_k}{R_{eq}} \times u uk=ReqRk×u<u
② 两个电阻的分压
u 1 = R 1 R 1 + R 2 , u 2 = R 2 R 1 + R 2 u_1=\frac{R_1}{R_1+R_2},u_2=\frac{R_2}{R_1+R_2} u1=R1+R2R1,u2=R1+R2R2
题目5:串联分压
1.6.2 电阻的并联
1. 电路特点:
① 各电阻两端为同一电压(KVL)
② 总电流等于流过各并联电阻的电流之和(KCL)
2. 等效电阻:
① 电导: 等效电导等于并联各电导之和
1 R e q = G e q = ∑ i = 1 k G i \frac{1}{R_{eq}}=G_{eq}=\sum_{i=1}^{k}G_i Req1=Geq=i=1∑kGi
② 电流: 并联电阻的分流(与电阻大小成反比)
i k = R e q R k i = G k G e q i i_k=\frac{R_{eq}}{R_k}i=\frac{G_k}{G_{eq}}i ik=RkReqi=GeqGki
电流分配与电导成正比,电阻成反比
③ 功率: 等效电阻消耗的功率等于各并联电阻消耗功率的总和
p = p 1 + p 2 + ⋯ + p k , p k = u 2 R k p = p_1+p_2+\dots+p_k,p_k=\frac{u^2}{R_k} p=p1+p2+⋯+pk,pk=Rku2
3. 两个电阻的分流:
I 1 = R 2 R 1 + R 2 , I 2 = R 1 R 1 + R 2 , I_1 = \frac{R_2}{R_1+R_2},I_2 = \frac{R_1}{R_1+R_2}, I1=R1+R2R2,I2=R1+R2R1,
1.6.3 电阻的串并联
电路中有电阻的串联,又有电阻的并联,这种连接方式称电阻的串并联。
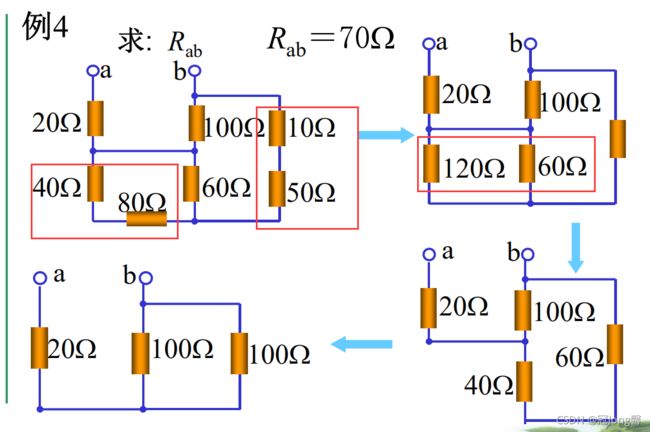
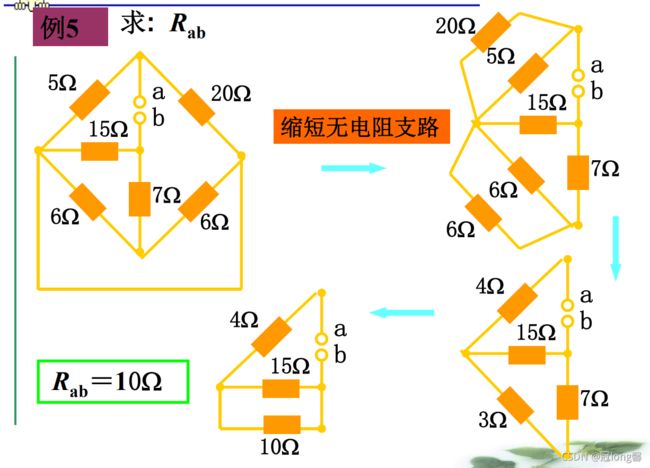
题目5:电阻的串并联等效
1.7 电压源的串联和并联
1.7.1 电压源的串联
u = u 1 + u 2 = ∑ u k u=u_1+u_2=\sum u_k u=u1+u2=∑uk
注意:注意参考方向
1.7.2 电压源的并联
u s = u s 1 = u s 2 u_s=u_{s1}=u_{s2} us=us1=us2
注意: 相同的电压源才能并联,电压源中的电流不确定
1.7.3 电压源与支路的串、并联等效
1. 串联:
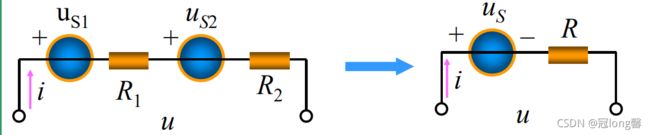
u = u s + i R e q u=u_s+iR_{eq} u=us+iReq
2. 并联:
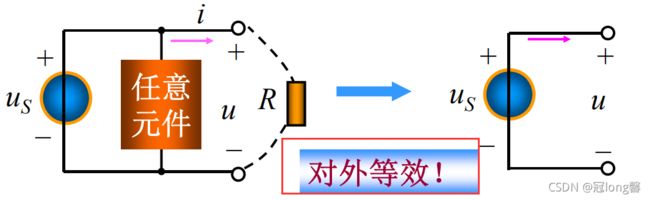
理解:与电压源并联的任一元件对外等效均可去除
1.8 电流源的串联和并联
1.8.1 电流源的并联
i s = ∑ i s i i_s=\sum i_{si} is=∑isi
1.8.2 电流源的串联
i s = i s 1 = i s 2 i_s=i_{s1}=i_{s2} is=is1=is2
注意:相同的电流源才能串联,每个电流源的端电压不确定
1.8.3 电流源与支路的串、并联等效
2. 并联:

i = i s − u R e q i=i_s-\frac{u}{R_{eq}} i=is−Requ
1.9 实际电源与两种电源模型的等效变换
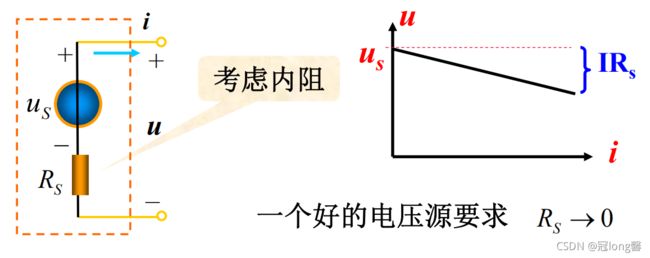
1.9.1 电压源模型
假设提供的实际电压u,内部提供的电压大小 u s u_s us,内阻 R s R_s Rs(串联)
u = u s − i R s u=u_s-iR_{s} u=us−iRs
1.9.2 电流源模型
假设提供的实际电压i,内部提供的电压大小 i s i_s is,内阻 R s R_s Rs(并联)
i = i s − u R s i=i_s-\frac{u}{R_s} i=is−Rsu

1.9.3 两种电源模型的等效变换
电压源、电流源两种模型可以进行等效变换。
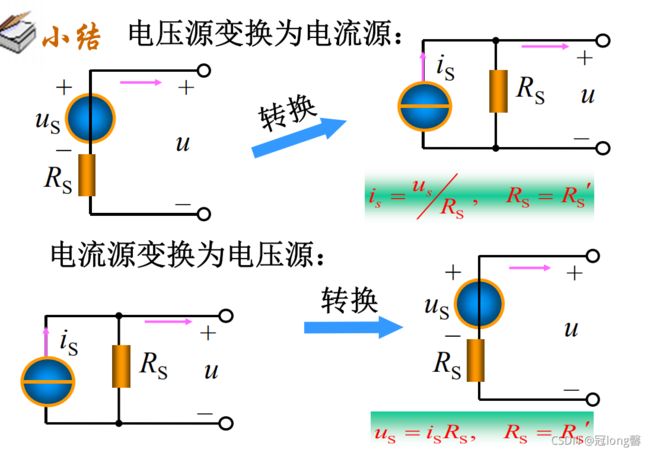
转换关系:
{ R s = R s ′ i s = u s R s \begin{cases} R_s = R_s' \\ i_s = \frac{u_s}{R_s} \end{cases} { Rs=Rs′is=Rsus
理解:电阻大小不变,串并联方式改变。 电压电流转换