loam算法_LOAM-SLAM原理深度解析
LOAM作为比较古老的激光匹配slam方法,一直以来都霸占着KITTI的前列,近些年来,依靠LOAM框架也产出了很多文章,理解了LOAM,就可以很好的理解LOAM系列的其他文章。
因此,我决定将重新整理一下LOAM的论文和代码,方便初入门的同学更好的理解LOAM算法。
论文:https://www.ri.cmu.edu/pub_files/2014/7/Ji_LidarMapping_RSS2014_v8.pdf
代码:https://github.com/HKUST-Aerial-Robotics/A-LOAM
文章较长,书写不易,如果觉得对您有帮助的话,希望可以点赞收藏支持一下哈~
1、论文概览
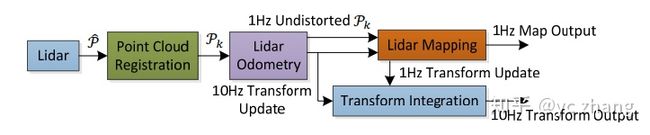
LOAM这篇论文是发表于2014年RSS的文章,全称为:LOAM: Lidar Odometry and Mapping in Real-time . LOAM是基于激光雷达而搭建的在ROS平台下的SLAM系统,一共分为四个部分:
本文的核心主要在于两个部分:特征提取(Lidar Registration)和里程计解算(Odometry and Mapping)。
当提取出特征后,通过两个高频率的里程计(Odometry)实现粗定位和低频率的里程计(Mapping)实现精定位。 下面,我们将结合论文和代码,进行LOAM框架的详细讲解。
2、符号设定
- 一个sweep代表了一次扫描周期,记作
- 一个扫描周期内获取到的所有点云记作
代表了第k个扫描周期的点云
- 雷达坐标系设定为
代表了第k个周期时的雷达观测坐标系,
在
中可以被表示为
- 全局坐标系设定为
代表了第k个周期时的全局坐标系,
在
中可以被表示为
因此,我们就可以将整个问题转化为:已知一段点云序列
3、Lidar Registration
为了计算雷达的运动位姿,我们需要得到的是相邻帧间的姿态变换关系,这样才能继续往后走下去。为了获取到相邻帧的姿态变换,使用全部点云处理是不可靠的,为了减少计算的时间消耗,一般需要使用特征点来代替完整的数据帧。
常见的特征点提取方法:特征向量、直方图、旋转图片等。
这些方法虽然能很精准的涵盖一帧数据的大部分信息,但是由于计算量大,很难在激光slam的相邻帧的匹配中使用。 因此,需要想一些更好的方法。
本文作者根据点的曲率来计算 平面光滑度作为提取当前帧的特征信息的指标。
这种提取方法就是通过计算一个集合
再得到平滑度这一指标后,可以将特征点划分为两大类:平面点和边缘点。
- 平面点:在三维空间中处于平滑平面上的点,其和周围点的大小差距不大,曲率较低,平滑度较低。
- 边缘点:在三维空间中处于尖锐边缘上的点,其和周围点的大小差距较大,曲率较高,平滑度较高。
我们对集合内的点进行排序,找到最小的点c作为平面点,最大的点c作为边缘点。
这样就可以在一帧中得到有效的点数了。而在论文中是对整个扫描进行化段,分四段,每段各取两个边缘点和4个平面点。而在A-LOAM的代码中则是进行了一下的实现:
同时,对所取的点也有一定的限制:
- 该点的周围的点尽量不要被再被取到,这样可以使整体的特征点分布更加的平均
- 该点不能与雷达扫描束过于平行,这样也会出现问题
具体样例如下图所示:
因此,选点就有了三要素:
- 不能超过设定的size,每个集合平面点4个,边缘点2个;
- 已选取的点周围不能有点,使得点可以分布的更加均匀;
- 选取的平面点不能与激光扫描束平行。
以上的对应关系,同样再代码中有着体现。
判断该点是否是之前选取的点的周围的点以及不能超过size:
通过上面的循环,就实现了边缘点(Corner)和平面点(Planar)的获取了。这样就可以得到一帧数据对应的特征信息了。
提取后的数据如图所示:
这样就可以在整个三维空间内,将平面点和边缘点作为特征点提取出来来代替整个数据了。
4、Lidar Odometry
再提取了特征点之后,我们需要做的就是特征匹配了。这里使用的使scan-to-scan的方法来实现帧与帧之间的特征匹配。
已知第
已知第
我们想要得到的是
由于雷达自身在
我们将重投影到每一帧初始时刻的平面点和边缘点记为:
这样的话就可以进行后续的优化了。
我们知道平面和边缘线是两种不同的特征,那么在LOAM的计算中,也是分开进行计算的。
4.1、边缘点匹配
已知信息:
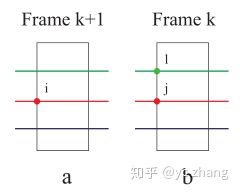
我们知道,边缘点就是三维结构中线所构成的点,这样的话,就是求点到线的最近距离。需要在
从
选取最近点的算法使用的是kd-tree的最近邻搜索,如果对kd-tree感兴趣的同学,可以阅读这篇文章: yc zhang:KD-Tree原理详解zhuanlan.zhihu.com
因此,选取了三个点: {
这样,就将姿态变换转换为了,点
因此,就变为了: 边缘点约束公式
我们知道,分子叉乘球出来的是
因此,我们就构建了边缘点的优化方程。
4.2、平面点匹配
已知信息
平面点的匹配起始和边缘点的匹配类似,同样的是寻找两帧之间的对应关系,我们知道平面点的话,就是要求点到平面的距离,这样的话,就需要在
从
因此,选取了四个点:{
这样的话,就变成了点
因此,就变为了: 平面点约束公式
故,分子为构成的三维物体的体积,分母为地面构成的平行四边形的面积,则高
因此,我们就得到了平面点的优化方程。
4.3、姿态解算
当获取到了
我们首先列出已知的信息:
由于考虑了雷达的自身运动是匀速运动,所以,我们获取了每个点的时间戳信息,并使用线性方程,得到每个时刻对应的姿态变换矩阵,这一步主要是进行了 运动补偿。
我们首先求解第
这样的话,就可以使用每个点对应的姿态变换矩阵放入进去进行后续的求解了。
但是,这里论文使用的是6-DoF的表示,也就是
所以,我们需要想办法从6-DoF得到对应的姿态变换矩阵,进行迭代优化求解。
我们设定旋转矩阵
这样的话,就可以构建公式:
这样,就可以将
这里就涉及到论文中所涉及到的几个符号的表示,建议可以对照论文当中来看。
- 核心思想就是要找到一个姿态变换使得可以将公式(2)和(3)中的右边部分进行化简计算,而我们知道{
},所以,需要将
转化到同样的帧中,统一坐标系,进行后面的解算。
回归正文,我们获得了得到了公式之后,就需要求解
然而,我们使用的是6-DoF的表示,就需要想办法进行欧拉角到旋转矩阵的变换,使用罗德里格斯公式进行变换: 欧拉角转旋转矩阵
PS:这里使用的是旋转向量来表示,而不是欧拉角。但是在原始的loam-velodyne版本中,我们使用的是欧拉角来进行后续的计算。而在后面的A-LOAM版本使用的是四元数来求解。也算是避开了原版的一个坑吧。
这样,就可以将欧拉角转换为旋转矩阵了,其中
而,平移矩阵就是6-DoF的前三位,也就是说
这样,就可以实现6-DoF和旋转矩阵的变动了。
那么我们可以知道在公式(2)和公式(3)中,只有
因此,可以统一为一个公式:
因此,我们就需要求解优化这个非线性优化问题就可以了。
那么使用常规的列文伯格-马夸特法(LM)来进行求解:
如果对最小二乘的求法感兴趣的话,我在这里总结了一些SLAM中最小二乘的求解方法: yc zhang:SLAM中最小二乘问题的求解方法zhuanlan.zhihu.com
和高斯牛顿法不一样的是,我们加入了信赖区域,
构建拉格朗日函数,
这样的话,化简后求导就可以得到:
我们化简后得到:
而
故,我们可以得到导数为:
我们可以看到,和论文中略有不同,这个和初始雅可比矩阵
代入梯度下降的公式为:
和论文中基本一致,就是表现的方式有一点点的区别。
不断求解上面这个式子,直到收敛即可。
代码使用的是ceres solver来进行求解。
首先设定损失函数:
然后设定代价函数:
最后是求解:
然后对球出来的数据进行迭代更新:
这样就可以实现优化求解了。
A-LOAM的代码相比于LOAM-Velodyne是使用了现有的优化求解库,这样可以使代码更加简介和简单,只需要输入边缘点对应关系的{
然而,需要注意的是:
这里求解的还是局部雷达观测坐标系下的结果,是为了求解相邻帧之间的变换,也就是
5、Lidar Mapping
当我们获取了若干相邻帧的姿态变换信息后,我们需要做的就是将其和全局地图进行匹配,并将其加入到全局地图之中。 mapping匹配示意图
这里设定:
- 第
帧之前的扫描点云在全局坐标系下的投影为
;
- 第
次扫描的末位,也就是
帧的起始时的姿态变换信息
。
- 利用Odometry的输出
,将
从
时刻的起始推演到
时刻的起始,得到姿态矩阵
。
- 通过
,将之前第
帧的点云投影到全局坐标系下,记为
。
这样,其实就很明晰了,我们需要做的就是优化求解
这里的已知信息为:{
同样是两个点云,求精准的姿态变换,这里和之前的Lidar Odometry部分很接近,所以,使用的算法基本相同。
不过,我们这里是 map-to-map的算法,所以,使用的
如果使用全部的地图数据,在计算效率上会大打折扣,所以,这里使用的是一个 边长为10m的立方体,用以代替全局地图,优化得到最终的姿态变换矩阵
选取特征点的方法是一样的,不过具体实现的方式不尽相同。
将
在这里,首先选取相邻点集合
- 平面点:
只保留平面特征点;
- 边缘点:
只保留边缘特征点。
计算
如果
如果
边缘线或平面块的位置通过穿过
可以清楚地看到,特征向量的长度反应了点的分布,也就是说我们根据特征值和特征向量就能计算出直线的方向。平面也是同理,我们可以根据两个较长的特征向量计算平面的法向量,三个向量相交于几何中心,这样平面就确定了。
通过这种方法就可以快速的确定对应的边缘线和平面了。
这样就可以快速的找到
这样就可以使用公式(2)和(3),利用 LM法来求解
后续可以通过VoxelFilter来进行降噪,减少点云的数量。
整个的计算流程可以表示如下: Lidar Mapping算法更新流程
通过不断的处理,就可以得到对应的了。
对应的代码解析如下:
对cube里的数据进行处理:
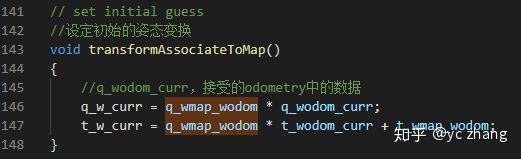
接受Lidar Odometry的数据,并得到初始的姿态变换矩阵:
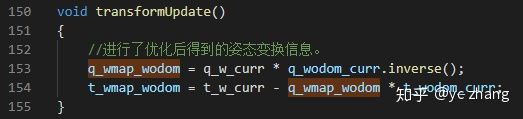
经过计算后,得到的新的姿态信息:
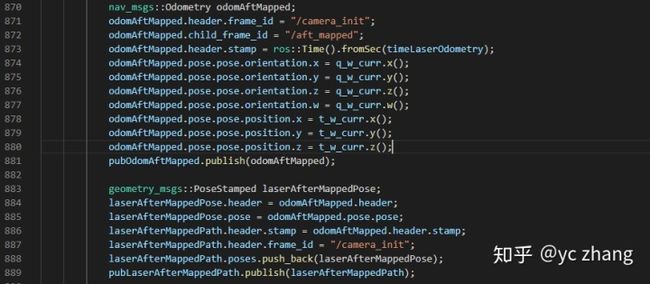
在这里,需要注意的是,我们最终传递的并不是q_wmap_odom和t_wmapodom。最终传递的是优化计算后得到的t_w_curr和q_w_curr:
Lidar Mapping节点publish的message6、Transform Integration
这一部主要是将Lidar Odometry中得到的姿态信息和Lidar Mapping中得到的信息全部都放入到rviz中,方便观看和处理。如果是为了使用LOAM作为前端的话,到Lidar Mapping就完全够用了。7、总结:
LOAM作为常见霸占KITTI榜的激光SLAM算法,是有着自己的独特优势的。其优缺点如下:优点:
- 新颖的特征提取方式(边缘点和平面点)
- 运动补偿(时间戳)
- 融合了scan-to-scan(odometry)和map-to-map(mapping)的思想
缺点:
- 没有后端优化(年代)
- 不能处理大规模的旋转变换(旋转向量的求解)
LOAM的整理到这里就结束了。LOAM由于发表时间较早,并没有进行后端优化。不过,他的后继者:LeGO-LOAM就很好的解决了这个问题。
yc zhang:LeGO-LOAM和LOAM的区别与联系zhuanlan.zhihu.com在LeGO-LOAM这篇文章中,我详细的阐述了LOAM和LeGO-LOAM的区别与联系,大家可以根据自己的实际需求选择对应的算法来实现想要的功能。
一路看下来,想必也不容易,如果觉得本文对您有帮助的话,希望可以点赞收藏关注支持一下哈~