机器学习实战笔记8——核方法

任务安排

1、机器学习导论       8、核方法
2、KNN及其实现      9、稀疏表示
3、K-means聚类      10、高斯混合模型
4、主成分分析          11、嵌入学习
5、线性判别分析      12、强化学习
6、贝叶斯方法          13、PageRank
7、逻辑回归              14、深度学习

核方法（KM）

Ⅰ 过拟合（Overfitting）

      在分类问题中，我们往往无法顺利地得到 $ACC=1.00$ 的分类器，会由于欠拟合的分类效果不够好，或是过拟合的方程阶数过高，非常难解（如图过拟合情况，一个拐点即一阶） 而导致分类效果不尽人意

      欠拟合，通常是线性分类器的简单划分所引起的弊端；而过拟合，通常是非线性分类器强大的学习能力导致的

Ⅱ 线性分类器

      线性分类器（Linear classifier），也称最大间隔分类器
      特点：
              1)分类速度快
              2)编程方便且便于理解
              3)但是拟合能力低
      我们已经学过的线性分类器有：LDA、朴素贝叶斯、逻辑回归
      以及后面要学的 SVM（线性核）

① 线性判别函数

      对于判别函数为如下函数形式的函数，可以认为该判别函数是线性的
      （在 线性回归 和 LDA 中有提到过，现在回顾也方便理解）$$g(x)=w^{T}x+{\omega }_0$$      其中 $x=[x_1,x2,...,x_d{]}^T$ 是 $d$ 维特征向量，又称样本向量，$w=[w_1,w_2,...,w_d{]}^T$ 称为权向量，${\omega }_0$ 是个常数，称为阈值权，对于二分类问题，线性分类器可以采取决策规则：

      令   $g(x)=g_1(x)-g_2(x)$

      如果$\{\begin{array}{l}g(x)＞0,则决策x\in {\omega }_1\\ g(x)＜0,则决策x\in {\omega }_2\\ g(x)=0,x归为任意一类，或拒绝\end{array}$

      方程 $g(x)=0$ 即一个决策面，$g(x)$ 为线性时， 即 $w^{T}x+{\omega }_0=0$ 是一个超平面
      假设 $x_i$ 和 $x_j$ 都在决策面 $H:g(x)=0$ 上，则有 $$w^T{x}_1+{\omega }_0=w^T{x}_2+{\omega }_0$$      即 $w^T(x_i-x_j)=0$，说明 $w$ 和超平面 $H$ 上任一向量正交，即 $w$ 是 $H$ 的法向量

      如图，对于任意向量 $x$，可以表示成如下形式$$x=x_p+r\frac{w}{||w||}$$
      其中，$x_p$ 是 $x$ 在 $H$ 上的射影向量（正投影），$r$ 是 $x$ 到 $H$ 的垂直距离（$x$ 终点到 $H$ 的距离），$\frac{w}{||w||}$ 是 $w$ 方向上的单位向量 （矢量三角形），将上式代入线性判别函数式可得$$g(x)=w^T(x_p+r\frac{w}{||w||})+{\omega }_0=w^T{x}_p+{\omega }_0+r\frac{w^{T}w}{||w||}=r||w||$$      即 $r=\frac{g(x)}{||w||}$（注意这里把 ${\omega }_0$ 省略了，因为 $x$ 会有穿过 $H$ 的情况，$r$ 表示的是 $H$ 正侧的距离），若 $x$ 是原点，则 $g(x)={\omega }_0$
      则原点到超平面的距离 $r_0=\frac{{\omega }_0}{||w||}$
      如果 ${\omega }_0>0$，则原点在 $H$ 正侧；若 ${\omega }_0<0$，则原点在 $H$ 负侧；若 ${\omega }_0=0$，则 $g(x)$ 具有齐次形式 $w^{T}x$，说明超平面 $H$ 通过原点
      总之，利用线性判别函数进行决策，就是用一个超平面把特征空间分割成两个决策区域。超平面的方向由权向量 $w$ 确定，位置由阈值权 ${\omega }_0$ 确定。判别函数 $g(x)$ 正比于 $x$ 点到超平面的代数距离（有正负号）。当 $x$ 在 $H$ 正侧时，$g(x)>0$；在负侧时，$g(x)<0$

② 最大间隔分类超平面

      对于如下例子，如果让我们随意画一条分类线，通常我们倾向于画类似 $A-B$ 这样的线，这是因为这条分类线离两类样本都最远

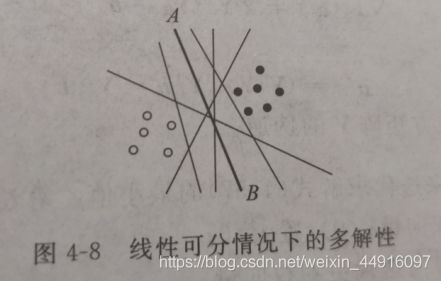
      下面用数学方法定义这样的分类线（面）
      对于训练样本集

                                    $(x_1),(x_2,y_2),...,(x_N,y_N)$      $x_i\in R^d,y_i\in${ $+1,-1$}

      每个样本都是 $d$ 维向量，$y$ 是类别标签，${\omega }_1$ 类用 +1 表示，${\omega }_2$ 类用 -1 表示，样本线性可分，即存在超平面      $$g(x)=(w\cdot x)+b$$      可以把所有 N 个样本没有错误地分开（$w\cdot x$ 即 $w^{T}x$）

定义：一个超平面，如果它能够将训练样本没有错误地分开，并且两类训练样本中离超平面最近的样本与超平面之间的距离是最大的，则把这个超平面称作最优分类超平面（optimal seperating hyperplane），也称最大间隔超平面，其中两类样本中离分类面最近的样本到分类面的距离称作分类间隔（margin）

      最优超平面定义的分类决策函数为$$f(x)=sgn(g(x))=sgn((w\cdot x)+b)$$      其中 $sgn()$ 为符号函数，当自变量为正时取1，负时取-1
      根据前面推导可知，向量 $x$ 到分类面 $g(x)=0$的距离是 $\frac{|g(x)|}{||w||}$
      对于上式分类决策函数，对权值 $w$ 和阈值权 $b$ 作任何正的尺度调整都不会影响分类决策，也不会改变样本到分类面的距离，因此上面定义的最优分类面没有唯一解，而有无数多个等价的解。为了使决策函数有唯一解，需确定 $w$ 和 $b$ 的尺度（目标是分类间隔最大化）
      所有N个样本都可以被超平面没有错误地分开，即$$\{\begin{array}{l}(w\cdot x_i)+b＞0，y_i=+1\\ (w\cdot x_i)+b＜0，y_i=-1\end{array}$$      调整 $w$ 和 $b$ 的尺度，则可以得到新的约束条件： $$\{\begin{array}{l}(w\cdot x_i)+b\ge 1，y_i=+1\\ (w\cdot x_i)+b\le -1，y_i=-1\end{array}$$      把样本类别标签乘到不等式里，则两式合并$$y_i[(w\cdot x_i)+b]\ge 1，i=1,2,...,N$$      满足此条件的超平面称为规范化的分类超平面，$g(x)=1$ 和 $g(x)=-1$ 是过两类中各自离规范化分类超平面最近的样本，且与规范化分类超平面平行的两个边界超平面，那么可以得到分类间隔 $M=\frac{2}{||w||}$，则

          目标函数：$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2$
          约束条件：$s.t.$       $y_i[(w\cdot x_i)+b]-1\ge 0，i=1,2,...,N$

      对于这类问题，可以用拉格朗日乘数法引入 ${\alpha }_i\ge 0，i=1,...,N$ 求解（但是目前的知识还不足以我们搞定），但根据结论可以知道，最终只有 $\alpha ＞0$ 的那部分样本决定了最优超平面的位置，故把这些样本称作支持向量（support vectors），由于最优超平面的解最后是完全由支持向量决定的，所以以上这种方法后来被称作支持向量机（support vector machines），缩写SVM

③ 线性不可分情况

      上述求解的最优超平面，仅仅是线性可分情况下的最优超平面，样本线性不可分时，上述定义的最优超平面不存在，那么，又该如何定义和求解新的支持向量机呢？
      样本线性不可分，即对于上式$$y_i[(w\cdot x_i)+b]-1\ge 0$$      样本集

                                    $(x_{,}{y}_1),(x_2,y_2),...,(x_N,y_N),$      $x_i\in R^d,y_i\in${ $+1,-1$}

      不同时满足，那么，需引入一个非负的松弛变量 ${\xi }_i，i=1,...,N$，约束条件变为$$y_i[(w\cdot x_i)+b]-1+{\xi }_i\ge 0$$      如果样本 $x_j$ 被正确分类，即 $y_j[(w\cdot x_j)+b]-1\ge 0$，则 ${\xi }_j=0$；若错分，即 $y_j[(w\cdot x_j)+b]-1＜0$，则 ${\xi }_j＞0$
      所有样本的松弛因子之和 ${\sum }_{i=1}^N{\xi }_i$ 可以反映整个训练样本集上的错分程度，因此，在线性可分的基础上，引入对错误的惩罚项，则广义最优分类面：
       目标函数：$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2+C(\stackrel{N}{\sum _{i=1}}{\xi }_i)$
       约束条件：$s.t.$       $y_i[(w\cdot x_i)+b]-1+{\xi }_i\ge 0，i=1,2,...,N$
                         ${\xi }_i\ge 0$      $i=1,2,...,N$

Ⅲ 非线性分类器

      非线性分类器（Nonlinear classifier）
      特点：
              ①拟合能力强
              ②编程实现复杂
              ③理解难度大
      已经学过的非线性分类器有：KNN
      以及接下来要学的 SVM（高斯核）

① 分段线性判别函数

      对于一个非线性函数，我们可以用多段线性函数来逼近（这里不是重点，就不展开了）

Ⅳ 支持向量机（SVM）

      在线性分类器里面，介绍了最优分类超平面，即线性的支持向量机，下面介绍非线性的支持向量机

① 广义线性判断函数

      如图，假定有一个二类问题，样本特征 $x$ 是一维的，决策规则是：若 $x＜a$ 或 $x＞b$，则 $x$ 属于 ${\omega }_1$ 类；如果 $b＜x＜a$，则 $x$ 属于 ${\omega }_2$ 类。显然，线性判别函数是无法实现该决策的，故需构造非线性分类器

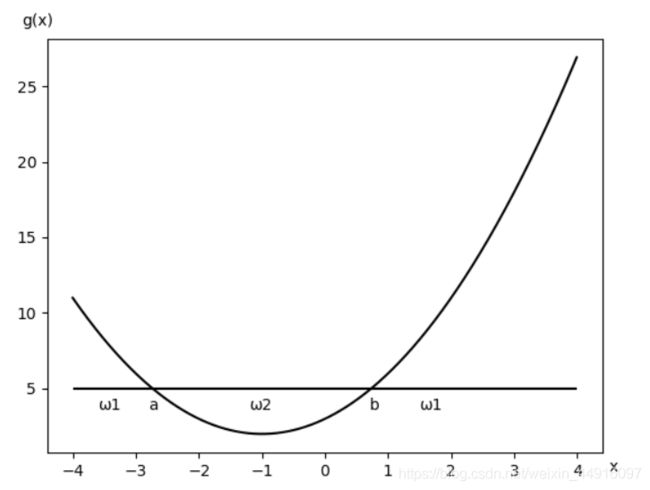
      对于该图，建立二次判别函数$$g(x)=(x-a)(x-b)$$      实现分类决策，则决策规则：
$$\{\begin{array}{l}g(x)＞0，x\in {\omega }_1\\ g(x)＜0，x\in {\omega }_2\end{array}$$      把二次判别函数写成 $g(x)=c_0+c_{1}x+c_2{x}^2$ 形式，再改写成矩阵的形式 $y=[y_1$ $y_2$ $y_3{]}^T$$=[1$ $x$ $x^2{]}^T$，$a=[a_1$ $a_2$ $a_3{]}^T$$=[c_0$ $c_1$ $c_2{]}^T$，则二次判别函数化为 $y$ 的线性函数 $g(x)=a^{T}y={\sum }_{i=1}^s{a}_i{y}_i$
      $g(x)=a^{T}y$ 称为广义线性判别函数，$a$ 叫做广义权向量，一般来说，对于任意高次判别函数 $g(x)$（这时的 $g(x)$ 可看作对任意判别函数作级数展开，然后取其截尾后的逼近），都可以通过适当变换，化为广义线性判别函数处理
      唯一的不足就是，通过这种变换，样本的维数大大增加了，极有可能陷入到 之前提到的 维数灾难问题，比如对于 200 维的原始特征，判别函数为四阶或五阶，变换后空间的维数会在 $10^9$ 以上，但是如果类比 PCA、LDA，把高维特征进行适当降维，解决维数灾难问题，该变换方法则十分可行

②核函数变换与支持向量机

      支持向量机就是一种引入特征变换将原空间的非线性问题转化成新空间的线性问题的方法，但它并没有直接计算这种复杂的非线性变换，而是采用了一种迂回方法间接实现

      对于上面提到的线性支持向量机，其分类决策函数为$$f(x)=sgn(w\cdot x+b)=sgn(\sum _{i=1}^n{\alpha }_i{y}_i(x_i\cdot x)+b)$$      （实际上 $w={\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i$，求解过程目前相关知识没学，直接搬了结论）对特征 $x$ 进行非线性变换，记新特征为 $z=\phi (x)$，则新特征空间里构造的支持向量机决策函数为$$f(x)=sgn(w^{\phi }\cdot z+b)=sgn(\sum _{i=1}^n{\alpha }_i{y}_i(\phi (x_i)\cdot \phi (x))+b)$$      比较发现，无论 $\phi (x)$ 具体形式如何，非线性变换对支持向量机的影响仅仅是把两个样本在原特征空间的内积 $(x_i\cdot x)$ 变成新空间的内积 $(\phi (x_i)\cdot \phi (x))$，新空间中的内积仍是原特征的函数，则$$K(x_i,x_j)\stackrel{def}{=}(\phi (x_i)\cdot \phi (x_j))$$      称为核函数，则变换空间里的支持向量机变为$$f(x)=sgn(\sum _{i=1}^n{\alpha }_i{y}_{i}K(x_i,x)+b)$$      对比线性支持向量机，这种通过内积实现的非线性支持向量机，只要知道了核函数 $K(x_i,x_j)$ 在计算难度上并没有实质性增加

④ 常见核函数

      1.多项式核函数$$K(x,x^{\prime })=((x\cdot x^{\prime })+1{)}^q$$      2.径向基（RBF）$$K(x,x^{\prime })=e^{(-\frac{||x-x^{\prime }|{|}^2}{{\sigma }^2})}$$      3.Sigmoid函数$$K(x,x^{\prime })=\tanh (v(x\cdot x^{\prime })+c)$$

今日任务

1.各个分类器的数据可视化
2.3.同之前的 17flowers、Digits、Face images、CIFAR10 数据集，多加一个支持向量机的分类性能测试

任务解决

1、这次作业难度不大，做法和之前的作业都差不多，就是SVM的核函数需要多尝试一下看下哪个效果更好，也可以尝试下线性回归的分类，但是因为返回的是连续的数值（并非类别标签 ），所以要设置一个阈值手动划分一下类别

代码

from sklearn.datasets import make_circles
from sklearn.neighbors import KNeighborsClassifier
from sklearn import naive_bayes, svm
from sklearn.linear_model import LogisticRegression, LinearRegression
import matplotlib.pyplot as plt
from myModule import clustering_performance

fig = plt.figure()

X_train, y_train = make_circles(n_samples=400, factor=0.5, noise=0.1)
X_test, y_test = make_circles(n_samples=400, factor=0.5, noise=0.1)


# 原图
plt.subplot(231)
plt.title('Original')
plt.scatter(X_train[:, 0], X_train[:, 1], marker='o', c=y_train)

# KNN
plt.subplot(232)
plt.title('KNN')

knn = KNeighborsClassifier(n_neighbors=30)
knn.fit(X_train, y_train)
y_predict_knn = knn.predict(X_test)
print('KNN: %.2f' % clustering_performance.clusteringMetrics1(y_test, y_predict_knn))

plt.scatter(X_test[:, 0], X_test[:, 1], marker='o', c=y_predict_knn)

# NaiveBayes
plt.subplot(233)
plt.title('NaiveBayes')

bayes = naive_bayes.GaussianNB()
bayes.fit(X_train, y_train)
y_predict_bayes = bayes.predict(X_test)
print('NaiveBayes: %.2f' % clustering_performance.clusteringMetrics1(y_test, y_predict_bayes))

plt.scatter(X_test[:, 0], X_test[:, 1], marker='o', c=y_predict_bayes)

# Logistic
plt.subplot(234)
plt.title('Logistic')

logistic = LogisticRegression(max_iter=500, solver='liblinear')
logistic.fit(X_train, y_train)
y_predict_logistic = logistic.predict(X_test)
print('Logistic: %.2f' % clustering_performance.clusteringMetrics1(y_test, y_predict_logistic))

plt.scatter(X_test[:, 0], X_test[:, 1], marker='o', c=y_predict_logistic)

lt.subplot(236)
plt.title('SVM')

# (kernel) It must be one of 'linear', 'poly', 'rbf', 'sigmoid', 'precomputed' or a callable
clf = svm.SVC(C=2, kernel='rbf', gamma=10, decision_function_shape='ovr')
clf.fit(X_train, y_train)
y_predict_svm = clf.predict(X_test)
print('SVM: %.2f' % clustering_performance.clusteringMetrics1(y_test, y_predict_svm))

plt.scatter(X_test[:, 0], X_test[:, 1], marker='o', c=y_predict_svm)

plt.show()

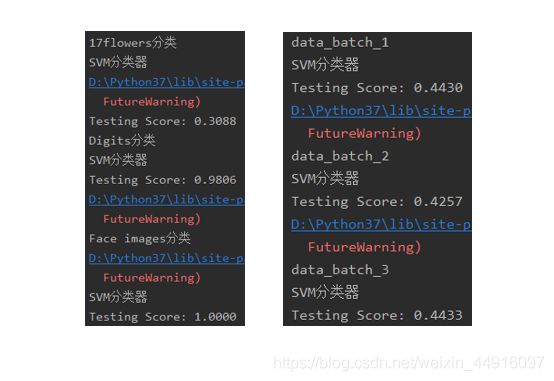
效果图

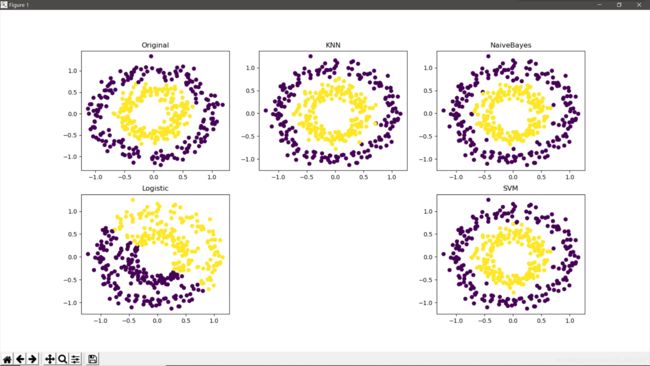
2、3、多跑了几次，发现性能会随样本集数量变多而比较明显地提高
代码2

from sklearn.datasets import load_digits
from sklearn import svm
from sklearn.model_selection import train_test_split
import numpy as np
import os
import cv2 as cv
from myModule import clustering_performance


def test_SVM(*data):
    X_train, X_test, y_train, y_test = data
    cls = svm.SVC(C=2, kernel='linear', gamma=10, decision_function_shape='ovo')
    cls.fit(X_train, y_train)
    y_predict_svm = cls.predict(X_test)
    print('SVM分类器')
    # print('Testing Score: %.4f' % cls.score(X_test, y_test))
    print('Testing Score: %.4f' % clustering_performance.clusteringMetrics1(y_test, y_predict_svm))
    return cls.score(X_test, y_test)


path_face = 'C:/Users/1233/Desktop/Machine Learning/face_images/'
path_flower = 'C:/Users/1233/Desktop/Machine Learning/17flowers/'


# 读取Face image
def createDatabase(path):
    # 查看路径下所有文件
    TrainFiles = os.listdir(path)  # 遍历每个子文件夹
    # 计算有几个文件(图片命名都是以 序号.jpg方式)
    Train_Number = len(TrainFiles)  # 子文件夹个数
    X_train = []
    y_train = []
    # 把所有图片转为1维并存入X_train中
    for k in range(0, Train_Number):
        Trainneed = os.listdir(path + '/' + TrainFiles[k])  # 遍历每个子文件夹里的每张图片
        Trainneednumber = len(Trainneed)  # 每个子文件里的图片个数
        for i in range(0, Trainneednumber):
            image = cv.imread(path + '/' + TrainFiles[k] + '/' + Trainneed[i]).astype(np.float32)  # 数据类型转换
            image = cv.cvtColor(image, cv.COLOR_RGB2GRAY)  # RGB变成灰度图
            X_train.append(image)
            y_train.append(k)
    X_train = np.array(X_train)
    y_train = np.array(y_train)
    return X_train, y_train


X_train_flower, y_train_flower = createDatabase(path_flower)
X_train_flower = X_train_flower.reshape(X_train_flower.shape[0], 180*200)
X_train_flower, X_test_flower, y_train_flower, y_test_flower = \
    train_test_split(X_train_flower, y_train_flower, test_size=0.2, random_state=22)

digits = load_digits()
X_train_digits, X_test_digits, y_train_digits, y_test_digits = \
    train_test_split(digits.data, digits.target, test_size=0.2, random_state=22)

X_train_face, y_train_face = createDatabase(path_face)
X_train_face = X_train_face.reshape(X_train_face.shape[0], 180*200)
X_train_face, X_test_face, y_train_face, y_test_face = \
    train_test_split(X_train_face, y_train_face, test_size=0.2, random_state=22)

print('17flowers分类')
test_SVM(X_train_flower, X_test_flower, y_train_flower, y_test_flower)
print('Digits分类')
test_SVM(X_train_digits, X_test_digits, y_train_digits, y_test_digits)
print('Face images分类')
test_SVM(X_train_face, X_test_face, y_train_face, y_test_face)

代码3

import pickle
import numpy as np
from sklearn import svm
from myModule import clustering_performance

path = 'C:/Users/1233/Desktop/Machine Learning/CIFAR10/cifar-10-batches-py/'


def unpickle(file):  # 官方给的例程
    with open(file, 'rb') as fo:
        cifar = pickle.load(fo, encoding='bytes')
    return cifar


def test_SVM(*data):
    X_train, X_test, y_train, y_test = data
    clf = svm.SVC(C=2, kernel='poly', gamma=10, decision_function_shape='ovr')
    clf.fit(X_train, y_train)
    y_predict_svm = clf.predict(X_test)
    print('SVM分类器')
    # print('Testing Score: %.4f' % clf.score(X_test, y_test))
    print('Testing Score: %.4f' % clustering_performance.clusteringMetrics1(y_test, y_predict_svm))
    # return clf.score(X_test, y_test)


test_data = unpickle(path + 'test_batch')
for i in range(1, 4):
    train_data = unpickle(path + 'data_batch_' + str(i))
    X_train, y_train = train_data[b'data'][0:3000], np.array(train_data[b'labels'][0:3000])
    X_test, y_test = test_data[b'data'][0:3000], np.array(test_data[b'labels'][0:3000])
    print('data_batch_' + str(i))
    test_SVM(X_train, X_test, y_train, y_test)

效果图