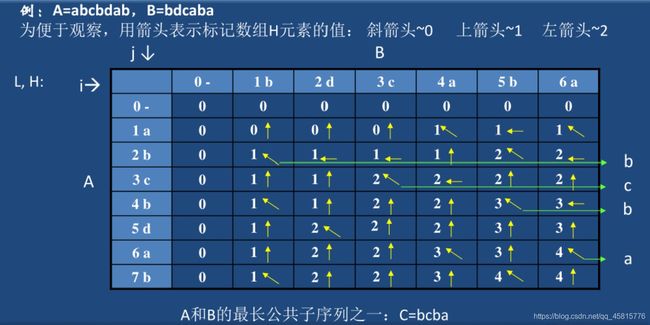
最长公共子序列 删除一些字符使得剩下字符为回文串

参考视频bilibil fjnuzs

---

一、分析

对于两个子序列，$a_1{a}_2\dots a_i,b_1{b}_2\dots b_j$L[i,j]表示他的最长公共子序列长度。为了得到这个长度，通常有两种情况，$a_i=b_j$那么长度是除这两个数以外的子串长度加一L[i, j]=L[i-1, j-1]+1;如果在比较的时候不相等，那么选一个已有的最长的L[i, j]=max{L[i-1, j], L[i, j-1]}。其实这里考虑的是递归的思想，但是我们可以通过分析发现，不就是L[i, j]记录上次的长度吗？递归到最底层的时候，长度都是0，就开始用这两种情况的式子一点一点把L二维数组填满，所以我们可以一行一行的填。

很容易知道，填满后最右下角一定是最长的距离了。但是如何去存储这个数组呢？在填表L的时候，我们多记录一个表H，L[i, j]=L[i-1, j-1]+1时将H[i, j]记录为0;L[i, j]=L[i-1, j]记录为1;L[i, j]=L[i, j-1]记录为2。

然后倒着从最右下角开始，是0就存在放最长公共子序列的数组里，是1就i-1，是2就j-1，最后到i=0,j=0就停止了。

二、伪代码

1.填表

输入: n、m、A= a...a、B=bpb..bm
输出: A和B的LCS长度L[n, m]和存储LCS有关信息的数组H[1..n, 1..m]
for i=0 ton L[i, 0]=0
forj=0 to m L[0, j]=0 //第一行第一列都是0
for i=1 to n
	forj=1 to m
		if a;=b; then
			L[i, j]=L[i-1,j-1]+1; H[i, j]=0
		else
			ifL[i-1, j]>=L[i,j-1] then L[i, j]=L[i-1,j]; H[i, j]=1
			else L[i, j]=L[i,j-1]; H[i, j]=2
return L[n, m], H
end LCS

2.获得序列

输入: n、m、A、B、H[1..n, 1..m]
输出:序列A和B的最长公共子序列C。
C=[]; i=n; j=m
while i>0 and j>0.
	if H[i, j]=0 then
		C=ai+C; i=i-1; j=j-1
	else
		if H[i, j]=1 then i=i-1 
		else j=j-1
return C
end LCSS

三、java实现

给定一个字符串s，你可以从中删除一些字符，使得剩下的串是一个回文串。如何删除才能使得回文串最长呢？输出需要删除的字符个数。还有这个回文是啥输出出来。

由于回文是首尾相同的，那么从头到尾和从尾到头的字符串他们的最长公共子序列就应该是留下的回文串。

import java.util.*;
public class Main {
     
	static int[][] L;
	static int[][] H;
	static String s1;
	static String s2;
	public static void main(String[] args) {
     
		Scanner sc = new Scanner(System.in);
		while (sc.hasNext()) {
     
			s1 = sc.next();
			s2 = new StringBuilder(s1).reverse().toString();
			L = new int[s1.length() + 1][s2.length() + 1];
			H = new int[s1.length() + 1][s2.length() + 1];
			for (int i = 1; i < L.length; i ++ ) {
     
				for (int j = 1; j < L[0].length; j ++ ) {
     
//					L[i][j] = s1.charAt(i - 1) == s2.charAt(j - 1) ? L[i - 1][j - 1] + 1 : Math.max(L[i - 1][j], L[i][j - 1]);
					if(s1.charAt(i - 1) == s2.charAt(j - 1)) {
     
						L[i][j] = L[i - 1][j - 1] + 1;
						H[i][j] = 0;
					}else {
     
						if(L[i - 1][j] > L[i][j - 1]) {
     
							L[i][j] = L[i - 1][j];
							H[i][j] = 1;
						}else {
     
							L[i][j] = L[i][j - 1];
							H[i][j] = 2;
						}
					}
				}
			}
			System.out.println("最少删除元素数量："+ (s1.length() - L[s1.length()][s2.length()]));
			
			//用栈来装吧，不用换顺序（虽然这道题回文本身顺序也无所谓）,而且长度也不用考虑了
			Stack<Character> st = new Stack<>();
			int j = s2.length(); 
			int i = s1.length();
			while(j>0 && i>0) {
     
				if(H[i][j] == 0) {
     
					st.add(s1.charAt(i-1));
					--i;
					--j;
				}else if(H[i][j] == 1) {
     
					--i;
				}else {
     
					--j;
				}
			}
			System.out.println(st);
		}
	}
	
}