PCL中3D点云特征描述与提取(一)
PCL中3D点云特征描述与提取(一)
- 1 特征描述与提取的概念及相关算法
-
- 1.1 3D形状内容描述子
- 1.2 旋转图像(Spin Images)
- 1.3 PCL中特征描述与提取模块及类
- 2 点云特征描述与提取入门级实例解析
-
- 2.1 PCL中描述三维特征相关基础
-
- 2.1.1 理论基础
- 2.1.2 输入点云调用习惯
- 2.2 估计一个点云的表面法线
-
- 2.2.1 理论基础
- 2.2.2 选择合适的尺度
- 2.2.3 法线估计实例详解
- 2.2.4 使用OpenMP加速法线估计
- 2.3 使用积分图进行法线估计
3D点云特征描述与提取是点云信息处理中最基础也是最关键的一部分,点云的识别、分割、重采样、配准、曲面重建等处理的大部分算法,都严重依赖特征描述与提取的结果。从尺度上来分,一般分为局部特征描述和全局特征描述,例如局部的法线等几何形状特征的描述,全局的拓扑特征描述,都属于3D点云特征描述与提取范畴。在PCL中,目前已有很多基本的特征描述子与提取算法,相信在PCL的快速发展下,将来会集成和添加更多特征描述子和提取算法。
本章首先对涉及的部分点云特征描述与提取的概念进行简介,由于特征描述子和提取算法的多样性,和实例相关的概念在后面结合实例也进行了详细介绍;其次对PCL的特征描述与提取相关模块及类进行简单介绍;最后通过应用实例来展示如何对PCL中特征描述与提取相关模块进行灵活运用,例如法线估计、各种点特征描述子的提取方法等。
1 特征描述与提取的概念及相关算法
1.1 3D形状内容描述子
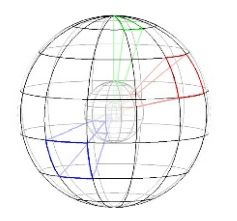
利用描述子建立曲面间的对应点在3D物体识别领域有广泛应用。采用一个向量描述曲面上指定点及其邻域的形状特征,通过匹配向量的值来建立不同曲面间点的对应关系,此向量即为指定点的描述子。3D形状内容描述子构造简单,辨别力强,且对噪声不敏感。其构造方法为:在以指定点p为中心的球形支撑域内,沿径向、方向角和俯仰角3个坐标方向划分成网格,统计落入网格内的点数,构造向量V。V的每个元素与支撑域内的一个网格对应,元素的值为对应网格中的点数,向量V即为点p的描述子。3D shape context网格划分如下图所示。详细内容请参考[Andrea Frome, Daniel Huber, Ravi Kolluri and Thomas Bulow, Jitendra Malik: Recognizing Objects in Range Data Using Regional Point Descriptors, In proceedings of the 8th European Conference on Computer Vision (ECCV), Prague, May 11-14, 2004]。
1.2 旋转图像(Spin Images)
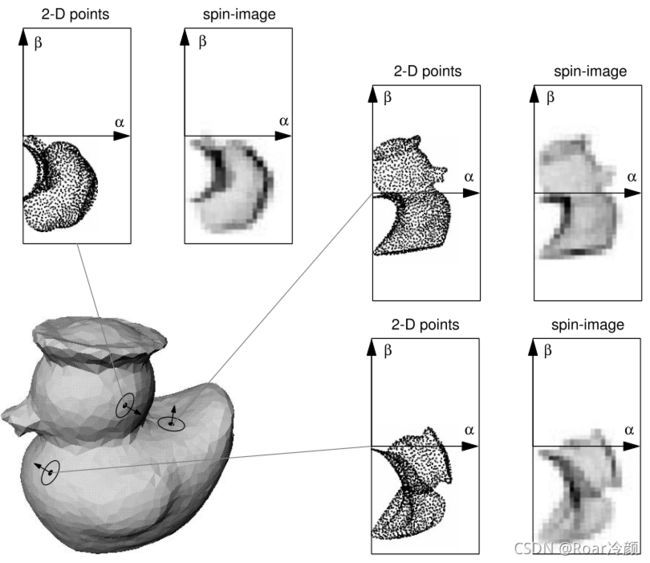
旋转图像最早是Johnson提出的特征描述子,主要用于3D场景中的曲面匹配和模型识别。如下面第一幅图所示,在模型表面上,存在顶点 p p p 和其法向量 n n n 定义的二维基,以及切平面 P P P,假设模型上任意顶点 x x x ,现定义 α \alpha α 为 x x x 在平面 P P P 上投影点与 p p p点的距离,规定其值取大于零的实数, β \beta β 为 x x x 与其在平面 P P P 上投影点之间的距离,按照向上或向下规定其有正负之分,点 p p p 的旋转图像则为,将除 p p p 点外其他模型上的顶点在 P P P 上的投影( α i \alpha _{i} αi, β i \beta _{i} βi),其中 i i i 表示顶点的一维索引,将( α i \alpha _{i} αi, β i \beta _{i} βi)统计得到二维直方图即为点 p p p 的旋转图像,图像的坐标由 α \alpha α 和 β \beta β 而定,强度为( α \alpha α, β \beta β)落在同一统计区间的点的统计个数。下面第二幅图所示模型表面三个点的旋转图像可帮助大家理解。

1.3 PCL中特征描述与提取模块及类
PCL中pcl_features库提供了特征描述与提取相关的基本数据结构与算法,目前PCL内部的特征提取算法包含基础和最新的点云或曲面模型相关的描述子实现,包括法线估计、多种基于近邻的局部描述算子、基于视角的全局描述算子等等,其依于common、search、kdtree、octree、range_image模块。类和函数的接口说明受篇幅所限,请感兴趣的读者自行查阅相关资料,或者查看官网。
2 点云特征描述与提取入门级实例解析
2.1 PCL中描述三维特征相关基础
本小节介绍点云库(PCL)中的三维特征描述子工作原理,以及在pcl::feature模块中类的通用调用习惯。
2.1.1 理论基础
在原始表示形式下,点的定义是用笛卡尔坐标系坐标 x x x, y y y, z z z 相对于一个给定的原点来简单表示的三维映射系统的概念,假定坐标系的原点不随着时间而改变,这里有两个点 p 1 p_{1} p1 和 p 2 p_{2} p2 ,分别在时间 t 1 t_{1} t1 和 t 2 t_{2} t2 捕获,有着相同的坐标。对这两个点做比较其实是属于不适定问题(ill-posed problem),因为虽然相对于一些距离测度(如:欧几里得度量)它们是相等的,但是它们取样于完全不同的表面,因此当把它们和邻近的其他环境中的点放在一起时,它们表达着完全不同的信息,这是因为在 t 1 t_{1} t1 和 t 2 t_{2} t2 之间局部环境有可能发生改变。一些获取设备也许能够提供取样点的额外数据,例如强度或表面反射率等,甚至颜色,然而那并不能完全解决问题,单从两个点之间来对比仍然是不适定问题。由于各种不同需求需要进行对比以便能够区分曲面空间的分布情况,应用软件要求更好的特征度量方式,因此作为一个单一实体的三维点概念和笛卡尔坐标系被淘汰了,出现了一个新的概念取而代之:局部描述子(local descriptor)。文献中对这一概念的描述有许多不同的命名,如:形状描述子(shape descriptor)或几何特征(geometric features),本文中剩余部分都统称之为点特征表示(point feature representations)。通过包括周围的邻域,特征描述子能够表征采样表面的几何性质,它有助于解决不适定的对比问题。如下图所示,理想情况下,相同或相似表面上的点的特征值将非常形似(相对特定度量准则),而不同表面上的点的特征描述子将有明显差异。下面几个条件,通过能否获得相同的局部表面特征值,可以判定点特征表示方式的优劣。
∙ \bullet ∙ 刚体变换(rigid transformations)—— 即三维旋转和三维平移变化不会影响特征向量F估计,即特征向量具有平移旋转不变性。
∙ \bullet ∙ 改变采样密度(varying sampling density)—— 原则上,一个局部表面小块的采样密度无论是大还是小,都应该有相同的特征向量值,即特征向量具有抗密度干扰性。
∙ \bullet ∙ 噪音(noise)—— 数据中有轻微噪音的情况下,点特征表示在它的特征向量中必须保持相同或者投其相似的值,即特征向量对点云噪声具有鲁棒性。
通常,PCL中特征向量利用快速kd tree查询,使用近似法来计算查询点的最近邻元素,有两种常用的查询类型。
(1)决定一个查询点的k邻域元素(k为用户已给参数)(也称为k-搜索)
(2)在半径r的围内,确定一个查询点的所有邻元素(也称为半径-搜索)
2.1.2 输入点云调用习惯
因为所有点云库中的类都继承来自基类pcl::PCLBase,pcl::Feature类接受以下两种不同方式的输入数据。
(1)一个完整的点云数据集,由setInputCloud (PointCloudConstPtr &) 给出——此函数必须设置,这样后续特征算子才能正常计算,任何可以进行特征描述子估计的类,为给定的输入点云中的每个点估计一个特征向量。
(2)点云数据集的一个子集,由setInputCloud (PointCloudConstPtr &) 和setIndices (IndicesConstPtr &) 给出——后面的setIndices 函数为可选设置。如果传入IndicesConstPtr 参数,则任何可以进行特征估计的类将为给定输入点云中的索引对应的点估计一个特征,默认情况下,如果没有给出一组索引,点云中的所有点参与计算。
此外,通过一个附加调用程序,可以明确指定搜索时使用的点邻域集合setSearchSurface (PointCloudConstPtr &),这个调用是可选的,当搜索点邻域集合未给出时,则输入点云数据为默认的搜索空间。因为总是需要 setInputCloud (),所以我们可以使用
∙ \bullet ∙ setIndices() = false, setSearchSurface() = false —— 毫无疑问这是点云库中最常用的情况,用户只需要输入一个单一的点云数据集,并且为点云中的所有点估计一特征向量。不论一组索引和(或)搜索点云是否给定,都不希望保存不同的实现副本,无论何时,即使indices = false,PCL都会创建一组内部索引(为 std::vector),这个索引集是指向整个数据集的(indices=1..N,N是点云中点的数目)。上述与图中最左边的情况对应,首先,我们估计了 p 1 p_{1} p1的最近邻元素,然后是 p 2 p_{2} p2的最近邻元素,以此类推,直到我们估计完 P P P中的所有点。
∙ \bullet ∙ setIndices() = true, setSearchSurface() = false —— 如前面所提到的,特征估计方法只计算已给索引的点的特征。对应上图的第二种情况,这里,我们假设 p 2 p_{2} p2的索引不在已给的索引向量中,因此在 p 2 p_{2} p2点处,没有估计邻元素或者特征向量。
∙ \bullet ∙ setIndices() = false, setSearchSurface() = true —— 如第一种情况,对所有已给点进行特征向量估计,但是,在setSearchSurface()中给出的采样面点云将用来为输入点获取最近邻元素,而不是输入点云本身,上述对应图中第三种情况。如果 Q = { q 1 , q 2 } Q = \left \{ q_{1}, q_{2}\right \} Q={ q1,q2}作为输入,是不同于 P P P的另一个给出的点云, P P P是 Q Q Q的搜索表面,那么将从 P P P中计算两个点 q 1 q_{1} q1和 q 2 q_{2} q2的近邻。
∙ \bullet ∙ setIndices() = true, setSearchSurface() = true —— 这种组合可能是最少见的情况,索引和搜索点云都给定。这种情况下,将使用setSearchSurface()中给出的搜索点云,只对
在使用 setSearchSurface()时,最有用的案例是:当有一个非常密集的输入点云数据集时,我们不想对它里面的所有点都进行特征估计,而是希望在找到的一些关键点处(使用pcl_keypoints中的方法进行估计),或者在点云的下采样版本中(如:使用pcl::VoxelGrid过滤而获得的)进行特征估计。这种情况下,我们通过setInputCloud()来把下采样后的点云/ 关键点传递给特征估计算法,而把原始数据通过setSearchSurface()设置为搜索集合,从而提高程序的运行效率。
2.2 估计一个点云的表面法线
表面法线是几何体表面的重要属性,在很多领域都有大量应用,例如:在进行光照渲染时产生符合可视习惯的效果时需要表面法线信息才能正常进行,对于一个已知的几何体表面,根据垂直于点表面的矢量,因此推断表面某一点的法线方向通常比较简单。然而,由于我们获取的点云数据集在真实物体的表面表现为一组定点样本,这样就会有两种解决方法。
(1)使用曲面重建技术,从获取的点云数据集中得到采样点对应的曲面,然后从曲面模型中计算表面法线。
(2)直接从点云数据集中近似推断表面法线。
本小节将针对后一种情况进行讲解,已知一个点云数据集,在其中的每个点处直接近似计算表面法线。
2.2.1 理论基础
尽管有许多不同的法线估计方法,本教程中着重讲解的是其中最简单的一个,表述如下:确定表面一点法线的问题近似于估计表面的一个相切面法线的问题,因此转换过来以后就变成一个最小二乘法平面拟合估计问题。
注意:更多信息,包含最小二乘法问题的数学方程式,可以查看相关文章 。
因此估计表面法线的解决方案就变成了分析一个协方差矩阵的特征矢量和特征值(或者PCA——主成分分析),这个协方差矩阵从查询点的近邻元素中创建。更具体地说,对于每一个点 P i P_{i} Pi,对应的协方差矩阵 C C C如下:
C = 1 K ∑ i = 1 K ( P i − P ˉ ) ( P i − P ˉ ) T , C ⋅ V ⃗ j = λ j ⋅ V ⃗ j , j ϵ { 0 , 1 , 2 } C = \frac{1}{K}\sum_{i=1}^{K}\left ( P_{i} - \bar{P}\right )\left ( P_{i} - \bar{P} \right )^{T},C\cdot \vec{V}_{j}=\lambda _{j}\cdot \vec{V}_{j}, j\epsilon \left \{ 0,1,2 \right \} C=K1i=1∑K(Pi−Pˉ)(Pi−Pˉ)T,C⋅Vj=λj⋅Vj,jϵ{ 0,1,2}
此处, K K K 是点 P i P_{i} Pi 邻近点的数目, P ˉ \bar{P} Pˉ 表示最近邻元素的三维质心, λ j \lambda _{j} λj 是协方差矩阵的第 j j j 个特征值, V ⃗ j \vec{V}_{j} Vj 是第 j j j 个特征向量。
在PCL内估计一点集对应的协方差矩阵,可以使用以下函数调用实现:
//定义每个表面小块的3x3协方差矩阵的存储对象
Eigen::Matrix3f covariance_matrix;
//定义一个表面小块的质心坐标16字节对齐存储对象
Eigen::Vector4f xyz_centroid;
//估计质心坐标
compute3DCentroid(cloud, xyz_centroid);
//计算3x3协方差矩阵
computeCovarianceMatrix(cloud, xyz_centroid, covariance_matrix);
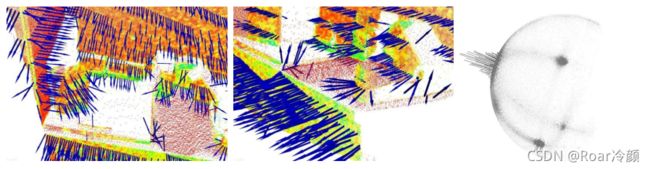
通常,没有数学方法能解决法线的正负向问题,如上所示,通过主成分分析法(PCA)来计算它的方向也具有二义性,无法对整个点云数据集的法线方向进行一致性定向。下图(1)中显示出对一个更大数据集的两部分产生的影响,此数据集来自于厨房环境的一部分,很明显估计的法线方向并非完全一致,图(2)部分展现了其对应扩展的高斯图像(EGI),也称为法线球体(normal sphere),它描述了点云中所有法线的方向。由于数据集是2.5维,其只从一个单一的视角获得,因此法线应该仅呈现出一半球体的扩展高斯图像(EGI)。然而,由于定向的不一致性,它们遍布整个球体,如下图所示。
如果实际知道视点 V p V_{p} Vp,那么这个问题的解决是非常简单的。对所有法线 V ⃗ j \vec{V}_{j} Vj 定向只需要使它们一致朝向视点方向,满足下面的方程式:
V ⃗ j ⋅ ( V p − P i ) > 0 \vec{V}_{j}\cdot \left ( V_{p}-P_{i} \right )>0 Vj⋅(Vp−Pi)>0
下图展示了上图中的数据集的所有法线被一致定向到视点后的结果:
在PCL中对一个已知点的法线进行手动重新定向,可以使用如下代码:
flipNormalTowardsViewpoint (const PointT &point, float vp_x, float vp_y, float vp_z, Eigen::Vector4f &normal)
注意:如果数据集是从多个捕获视点中配准后集成的,那么上述法线的一致性定向方法就不适用了。需要使用更复杂的算法,可以查看文章。
2.2.2 选择合适的尺度
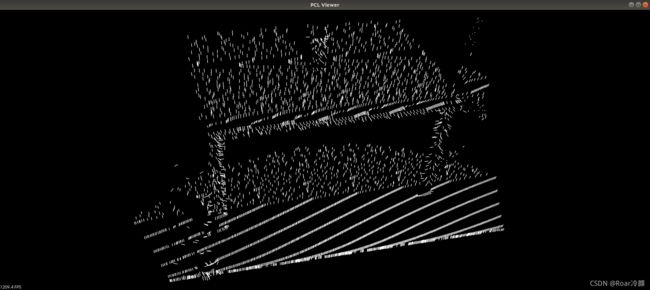
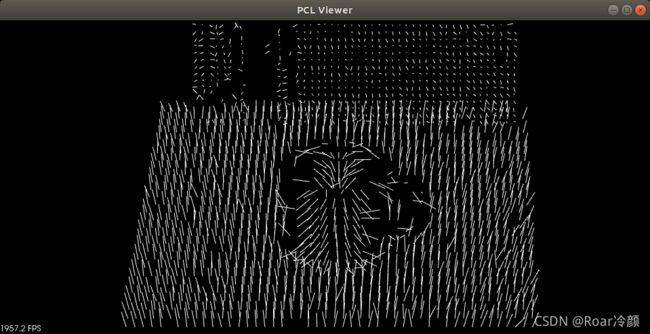
如之前介绍的,在估计一个点的表面法线时,我们需要从周围支持这个点的邻近点着手(也称作k邻域)。最近邻估计问题的具体内容又提出了另一个问题“合适的尺度”:已知一个取样点云数据集,k的正确取值是多少(k通过pcl::Feature::setKSearch给出)或者确定一个点r为半径的圆内的最近邻元素集时使用的半径r该取什么值(r通过pcl::Feature::setRadiusSearch给出)。这个问题非常重要,并且在一个点特征算子的自动估计时(例如用户没有给定阈值)是一个限制因素。为了更好地说明这个问题,以下图示表现了选择更小尺度(如:r值或k取相对小)与选择更大尺度(如:r值或k值比较大)时的两种不同效果,下面两幅图分别为近视图和远视图,两图中左边部分展示选择了一个合理的比例因子,估计的表面法线近似垂直于两个平面,即使在互相垂直的边缘部分,可明显看到边缘。如果这个尺度取得太大(右边部分),这样邻近点集将更大范围地覆盖邻近表面的点,估计的点特征表现就会扭曲失真,在两个平面边缘处出现旋转表面法线,以及模糊不清的边界,这样就隐藏了一些细节信息。
无法深入探究更多讨论,现在可粗略假设,以应用程序所需的细节需求为参考,选择确定点的邻域所用的尺度。简言之,如果杯子手柄和圆柱体部分之间边缘的曲率是重要的,那么需要足够小的尺度来捕获这些细节信息,而在其他不需要细节信息的应用中可选择大的尺度。
2.2.3 法线估计实例详解
首先创建一个工作空间normal_estimation,然后再在工作空间创建一个文件夹src用于存放源代码:
mkdir -p normal_estimation/src
接着,在normal_estimation/src路径下,创建一个文件并命名为normal_estimation.cpp,拷贝如下代码:
#include 法线估计类NormalEstimation的实际计算调用内部程序执行以下操作。
(1)对点 P P P 中的每个点,得到 p p p 点的最近邻元素
(2)计算 p p p 点的表面法线 n n n。
(3)检查 n n n 的方向是否一致指向视点,如果不是则翻转。
视点坐标默认为(0,0,0),可以使用以下代码进行更换:
setViewPoint (float vpx, float vpy, float vpz)
计算单个点的法线,使用:
computePointNormal(const pcl::PointCloud<PointInT> &cloud, const std::vector<int> &indices, Eigen::Vector4f &plane_parameters, float &curvature)
此处,cloud是包含点的输入点云,indices是点的k-最近邻元素集索引,plane_parameters和curvature是法线估计的输出,plane_parameters前三个坐标中, 以(nx,ny,nz)来表示法线。输出表面曲率curvature通过协方差矩阵的特征值之间的运算估计得到。
【编译和运行程序】
在工作空间根目录normal_estimation下,编写CMakeLists.txt文件如下:
cmake_minimum_required(VERSION 2.8 FATAL_ERROR)
project(normal_estimation)
find_package(PCL 1.2 REQUIRED)
include_directories(${
PCL_INCLUDE_DIRS})
link_directories(${
PCL_LIBRARY_DIRS})
add_definitions(${
PCL_DEFINITIONS})
add_executable (${
PROJECT_NAME}_node src/normal_estimation.cpp)
target_link_libraries (${
PROJECT_NAME}_node ${
PCL_LIBRARIES})
在工作空间根目录normal_estimation下创建一个build文件夹,用于存放编译过程中产生的文件,然后执行编译:
mkdir build
cd build
cmake ..
make
此时,会在build文件夹下生成一个可执行文件normal_estimation_node,运行该可执行文件:
./normal_estimation_node
运行上述命令后,可以在3D可视化窗口中看到如下效果:
上述代码片段估计了输入数据集中所有点的一组曲面法线,可以对上述代码稍微修改,从而只为输入数据集中的一部分点估计一组曲面法线。修改之后的代码如下所示:
#include 上述代码中创建原始输入点云的一个子集索引,取前50%,然后利用 setIndices 函数把子集的索引传递给法线估计对象,这样求解出来的就是这一组子集所对应的曲面法线,结果如下所示:
最后,下面的代码片段将为输入数据集中的所有点估计一组曲面法线,但将使用另一个数据集估计它们的最近邻:
#include 在上述代码中,利用 setInputCloud 函数把下采样后的点云数据传递给法线估计对象,然后利用 setSearchSurface 函数传递原始数据(下采样之前的点云数据)作为搜索点云,最终可视化结果如下所示:

2.2.4 使用OpenMP加速法线估计
对于对运算速度有要求的用户,PCL点云库提供了一个表面法线的附加实现程序,它使用多核/多线程开发规范,利用OpenMP来提高计算速度。它的类命名为pcl::NormalEstimationOMP,并且它的应用程序接口(API)100%兼容单线程pcl::NormalEstimation,这使它适合作为一个可选提速方法。在8核系统中,可以轻松提速6-8倍。
2.3 使用积分图进行法线估计
本小节我们将学习如何使用积分图(integral images)计算一个有序点云的法线,注意该方法只适用于有序点云。
首先创建一个工作空间normal_estimation_using_integral_images,然后再在工作空间创建一个文件夹src用于存放源代码:
mkdir -p normal_estimation_using_integral_images/src
接着,在normal_estimation_using_integral_images/src路径下,创建一个文件并命名为normal_estimation_using_integral_images.cpp,拷贝如下代码:
#include 【解释说明】
上述代码的第一部分,我们从文件中加载了一个点云存储在点云对象,以备后续作为法线估计对象的输入:
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
pcl::io::loadPCDFile ("../pcd/table_scene_mug_stereo_textured.pcd", *cloud);
在第二部分中,定义了存储估计法线的点类型指针,并为创建了一个积分图法线估计的对象ne设置对象计算时需要的参数,例如估计方法、点云等:
pcl::PointCloud<pcl::Normal>::Ptr normals (new pcl::PointCloud<pcl::Normal>);
pcl::IntegralImageNormalEstimation<pcl::PointXYZ, pcl::Normal> ne;
ne.setNormalEstimationMethod (ne.AVERAGE_3D_GRADIENT); // 设置估计方法
ne.setMaxDepthChangeFactor(0.02f); // 最大深度变化系数
ne.setNormalSmoothingSize(10.0f); // 优化法线方向时考虑邻域大小
ne.setInputCloud(cloud); // 输入点云,必须为有序点云
ne.compute(*normals); // 执行法线估计,存储结果到 normals
以下是可使用的法线估计方法:
enum NormalEstimationMethod
{
COVARIANCE_MATRIX,
AVERAGE_3D_GRADIENT,
AVERAGE_DEPTH_CHANGE
}
COVARIANCE_MATRIX模式从具体某个点的局部邻域的协方差矩阵创建9个积分图,来计算这个点的法线。AVERAGE_3D_GRADIENT模式创建了6个积分图来计算水平和垂直方向平滑后的三维梯度,并使用两个梯度间的向量积计算法线。AVERAGE_DEPTH_CHANGE模式只创建了一个单一的积分图,并从平均深度变化计算法线。
【编译和运行程序】
在工作空间根目录normal_estimation_using_integral_images下,编写CMakeLists.txt文件如下:
cmake_minimum_required(VERSION 2.8 FATAL_ERROR)
project(normal_estimation_using_integral_images)
find_package(PCL 1.2 REQUIRED)
include_directories(${
PCL_INCLUDE_DIRS})
link_directories(${
PCL_LIBRARY_DIRS})
add_definitions(${
PCL_DEFINITIONS})
add_executable (${
PROJECT_NAME}_node src/normal_estimation_using_integral_images.cpp)
target_link_libraries (${
PROJECT_NAME}_node ${
PCL_LIBRARIES})
在工作空间根目录normal_estimation_using_integral_images下创建一个build文件夹,用于存放编译过程中产生的文件,然后执行编译:
mkdir build
cd build
cmake ..
make
此时,会在build文件夹下生成一个可执行文件normal_estimation_using_integral_images_node,运行该可执行文件:
./normal_estimation_using_integral_images_node
运行上述命令后,可以在3D可视化窗口中看到如下效果:
从上图可以看出,法线方向基本一致朝向视点,视图视点朝向场景中的桌面,桌面上的杯子处出现平行于桌面的法线,而桌面上的点集的法线都垂直于桌面并指向点云本身获取时的视点,利用此方法进行法线估计只适用于有序点云,对于无序点云就只能采用其他方法了。