红书《题目与解读》第一章 数学 题解《ACM国际大学生程序设计竞赛题目与解读》

整理的算法模板合集： ACM模板

点我看算法全家桶系列！！！

实际上是一个全新的精炼模板整合计划

---

红书《题目与解读》第一章 数学 题解《ACM国际大学生程序设计竞赛题目与解读》

全书目录：《题目与解读》红书 训练笔记目录《ACM国际大学生程序设计竞赛题目与解读》

第一章 数学

1.1 概率

Problem A.Coupons （几何概型，概率）

UVA 10288

Problem

一共有 $n$ 种不同的优惠券，每次得到一个优惠券的概率相同，问期望多少次得到所有 $n$ 种优惠券，以带分数的形式输出。

Solution

方法一：

设 $f[i]$ 表示已经买到 $i$ 个优惠券的期望购买次数。

考虑最后一次购买，若买到的是一个新优惠券，则：

$$f[i]+=(f[i-1]+1)\times \frac{n-(i-1)}{n}$$

若买到的是一个已经买过但不是第 $i$ 个买的优惠券，则：

$$f[i]+=(f[i]+1)\times \frac{i-1}{n}$$​

整理得：

$$f[i]=f[i-1]+\frac{n}{n-i+1}$$​

即：

$$ans=\sum _{i=1}^n\frac{n}{n-i+1}=\sum _{i=1}^n\frac{n}{i}$$

显然最后的答案就是调和级数前缀和。

若数据较大的话可以 $O(1)$ 计算调和级数前缀和：

调和级数 $\sum _{i=1}^{\infty }\frac{1}{n}$ 的极限为 $\ln n+C$，其中 $C=0.57721566490153286060651209$ 是欧拉常数

方法二：

红书上的题解

当前已有 $k$ 种，显然得到新优惠券的概率为 $\frac{n-k}{n}$，显然是几何概型，所以期望是 $\frac{n}{n-k}$，所以答案就是 $\frac{n}{n}+\frac{n}{n-1}+\cdots +\frac{n}{1}=n\times \sum _{i=1}^n\frac{1}{i}$

Hint

数据较大，注意约分，除掉 $\gcd$

Code

#include 
#define int long long
using namespace std;
//#define ll __int128;
typedef long long ll;
const int N = 107;

int n, m;
int up[N], down[N]; 

ll lcm(int a, int b)
{
     
	return a / __gcd(a, b) * b;
}

int get_len(int x)
{
      
	int len = 0;
	while(x) {
     
		x /= 10;
		len ++ ;
	}
	return len;
}

void solve()
{
     
	ll LCM = 1;
	for(int i = 1; i <= n; ++ i) {
     
		up[i] = n;
		down[i] = i;
		LCM = lcm(LCM, i);
	}	
	ll sum = 0;
	for(int i = 1; i <= n; ++ i) {
     
		sum += n * (LCM / i);
	}
	ll d = __gcd(sum, LCM);
	sum /= d;
	LCM /= d;
	if(LCM == 1) {
     
		cout << sum << endl;
		return ;
	}
	ll mo = sum % LCM;
	ll l = sum / LCM;
	for(int i = 1; i <= get_len(l) + 1; ++ i) cout << " ";
	cout << mo << endl;
	cout << l << " ";
	for(int i = 1; i <= get_len(LCM); ++ i) cout << "-";
	puts("");
	for(int i = 1; i <= get_len(l) + 1; ++ i) cout << " ";
	cout << LCM << endl;
}

signed main()
{
     
	while(scanf("%lld", &n) != EOF) {
      
		solve();
	}
	return 0;
}

Problem B.Generator （KMP，期望，高斯消元）

ZOJ 2619

Problem

给定一个字符串 $S$ 和字符集大小 $n$ 。要求另生成一个字符串，它一开始为空，每次平均且独立地随机生成一个字符集中的字符添加到其末尾，生成出字串 $S$ 时停下，求所生成字符串的长度的期望。

Solution

显然生成的字符串越来越长，每次由 $n$ 种字符选择，那么就有 $i^n$ 种方案数，杂乱无章的无从下手。所以从对答案的贡献角度出发，发现对于答案而言，有用的只有最后生成的字符串 $T$ 的后缀与模式串 $S$ 的匹配长度。因此很多杂乱的字符串实际上对于答案而言是同一种状态，即一共只有 $0\sim L$ 种状态，表示两字符串匹配的长度。

这样就有了清晰的状态，考虑状态如何转移即可。

书中倒推由于都是未知的需要使用高斯消元解方程组，比较麻烦，精度还不能得到保障。我们这里利用一个小技巧，直接正推。利用 KMP ，$O(n)$ 求出失配数组 ${\text{nex}}_{i,j}$（当然要在失配的时候用）

反过来设 f[i] 为从状态 $0$ 到状态 $i$ 期望次数，答案显然就是 f[len]

则可以把原转移方程直接改写为：

$$f[i]=\frac{f[i+1]}{n}+\frac{1}{n}\sum _{j=0}^{n-1}f[\text{nex}[i{+}^{\prime }A{}^{\prime }]]-1$$
就是 $f[i]$ 由下一步匹配成功的 $f[i+1]$ 与未匹配成功的 $\sum _{j=0}^{n-1}f[\text{nex}[i{+}^{\prime }A{}^{\prime }]]$ 减去一次期望操作转移而来。

化简成正推的形式即：
$$f[i+1]=(f[i]+1)\times n-\sum _{j=0}^{n-1}f[\text{nex}[i{+}^{\prime }A{}^{\prime }]]$$

初始化 f[0] = 0，然后 $O(n)$ 正序递推即可。

Code

#include 

using namespace std;
using ll = long long;
const int N = 50;

int n, m, k, t, ans, kcase, cases;
int a[N];
int nex[N];
char s[N];
ll f[N];
int len;

void get_nex(char* s)
{
      
	for (int i = 2, j = 0; i <= len; ++ i) {
     
		while(j != 0 && s[j + 1] != s[i])
			j = nex[j];
		if(s[j + 1] == s[i])
			++ j;
		nex[i] = j;
	}
}

void solve()
{
      
	scanf("%d%s", &n, s + 1);
	len = strlen(s + 1);
	get_nex(s);
	f[0] = 0;
	for (int i =0; i <= len - 1; ++ i) {
     
		f[i + 1] = (f[i] + 1) * n;
		for (int j = 0; j < n; ++ j) {
     
			if(s[i + 1] == 'A' + j) 
				continue; 
			int pos = i;
			while(pos && s[pos + 1] != j + 'A')
				pos = nex[pos];
			if(s[pos + 1] == j + 'A')
				++ pos;
			f[i + 1] -= f[pos];
		}
	}
	printf("%lld\n", f[len]);
}

int main()
{
     
	scanf("%d", &t); 
	while(t -- ) {
     
		printf("Case %d:\n", ++ kcase);
		solve();
		if(t)
		    puts("");
	}
	return 0;
}

Problem C.Dinner with Schwarzenegger!!! （概率）

UVA10217

Problem

有若干人排队买电影票，如果某个人的生日与排在他前面的某个人的生日相同，那么他讲中奖。中奖的机会只有一个，给所有中奖者中排在最前面的那一位。排在第一位的人如果与买票者的生日相同，那么他将中奖。如果一年有 $n$ 天，求排在什么位置的中奖概率最大，和理论上的最佳实数位置。

Solution

设第 $i$ 个人的中奖概率是 f[i]，显然有：

$$f[1]=\frac{1}{n}$$

$$f[2]=\frac{n-1}{n}\times \frac{1}{n}$$

$$...$$

$$f[i]=\frac{n-1}{n}\times \frac{n-1}{n}\times \frac{n-2}{n}\times ...\times \frac{n-i+2}{n}\times \frac{i-1}{n}$$

$$f[i+1]=\frac{n-1}{n}\times \frac{n-1}{n}\times \frac{n-2}{n}\times ...\times \frac{n-i+1}{n}\times \frac{i}{n}$$

有

$$\frac{f[i]}{f[i+1]}=\frac{(i-1)\times n}{(n-i+1)\times i}$$

显然概率越来越小， $\frac{f[i]}{f[i+1]}\ge 1$ 解得：

$$\frac{1-\sqrt{4\times n+1}}{2}\le i\le \frac{1+\sqrt{4\times n+1}}{2}$$

最佳整数位置为 $\lceil \frac{1+\sqrt{4\times n+1}}{2}\rceil$，最佳实数位置为 $\frac{-1+\sqrt{4\times n+1}}{2}$。

Code

#include 
using namespace std;
const int maxn = 1e5 + 7, maxm = maxn << 1 | 7;

int n, m, s, t;
int a[maxn];

int main()
{
     
	while(scanf("%d", &n) != EOF) {
     
		double ans = (-1.0 + sqrt(1.0 + 4.0 * n)) / 2.0;
		int ans2 = ans + 1;
		printf("%.2lf %d\n", ans, ans2);
	}
	return 0;
}

1.2 代数

1.2.1 Polya

Problem A.Arif in Dhaka （Polya，等价类计数）

UVA 10294

Problem

给你一串珠子（连接成了一个环），共有 $n$ 个珠子组成，你有 $t$ 种颜色，现在你来给这个珠子染色，问染成项链有多少种方法？染成手镯有多少种方法？在项链里，经过顺时针旋转后相同的算一个，在手镯里，经过顺时针旋转或者沿着对称轴兑换后一样的算一个。

Solution

Code

1.2.2 矩阵

Problem A.Tower

HDU 2971

Problem

$a_1=1$，给定 $a_2$，设 $a_n=2a_2\times a_{n-1}-a_{n-2}$，求 $s_n=a_1^2+a_2^2+\cdots +a_n^2$。

Solution

设 $p=a_2\times 2$

则有：

$$a_n^2=p^2\times a_{n-1}+a_{n-2}^2-2\times p\times a_{n-1}\times a_{n-2}$$

$$s_n=s_{n-1}+a_n^2=s_{n-1}+p^2\times a_{n-1}^2+a_{n-2}^2-2\times p\times a_{n-1}\times a_{n-2}$$

可以发现重复项 $a_{n-1}^2$ 与 $a_{n-1}\times a_{n-2}$，可得：
$$a_n\times a_{n-1}=p\times a_{n-1}^2-a_{n-1}\times a_{n-2}$$

由不变项可得：

$$\left(\begin{array}{c}{S}_n\\ a_n^2\\ a_{n-1}^2\\ a_n\times a_{n-1}\end{array}\right)=\left(\begin{array}{cccc}1& p^2& 1& -2p\\ 0& p^2& 1& -2p\\ 0& 1& 0& 0\\ 0& p& 0& -1\end{array}\right)\left(\begin{array}{c}{S}_{n-1}\\ a_{n-1}^2\\ a_{n-2}^2\\ a_{n-1}\times a_{n-2}\end{array}\right)$$

Problem B.XX Language

ZOJ 2113

1.2.3 线性方程组

Problem A. Ars Longa

UVALive 3563

1.2.4 线性规划

Problem A.Expensive Dirnk

HDU 2979

1.3 组合

1.3.1 基本排列组合

The Unreal TournamentUVA 10207

1.3.2 容斥原理

Jackpot Gym 101648J
The Almost Lucky Number SCU 3502

1.3.3 生成函数

Vasya’s Dad URAL 1387

1.3.4 生成树计数

Organising the OrganisationUVA 10766

1.3.5 综合

Hero of Our TimeSGU 481

1.4 博弈

Problem A. Battle for the Ring（SG函数）

URAL 1540

Problem

给你一堆石子，每个石子都有权重，每次取一堆中的一个石子，将这堆石子中所有权重比该石子小的全部拿掉，分成若干堆新石子，不能操作的输。

Solution

Problem B. Fool’s Game

POJ 3153

Problem

Solution

Problem C. Points Game

URAL 1397

Problem

给出平面 $2n$ 点，有两个玩家游戏。每个回合，玩家A可以取走一个点，然后玩家B取走一个。经过 $n$ 个回合没有点了，结束比赛。一个玩家的得分是他所取走的所有两两之间的欧几里得距离的和，得分最高者获胜。A和B都是聪明人，求两者分数之差为多少。

Solution

1.5 数论

1.5.1 模线性方程

Problem A.Integer Sequences （多变元线性同余方程）

SGU 140

Problem

给出一个长度为 $n$ 的非负整数序列 $A$ 和两个数 $P,B$，要求找出同样的非负整数序列 $X$ 满足 $A_1\ast X_1+A_2\ast X_2+...+A_n\ast X_n=B(\mathrm{m}\mathrm{o}\mathrm{d}P)$

Solution

$$A_1\ast X_1+A_2\ast X_2+...+A_n\ast X_n=B(\mathrm{m}\mathrm{o}\mathrm{d}P)$$

显然有
$$A_1\ast X_1+A_2\ast X_2+...+A_n\ast X_n+PQ=B,Q\in \mathbb{Z}$$

看起来是一个多元一次方程，我们只需要找到一个合法的非负整数序列 $X$ 作为解即可，因此我们可以构造答案。我们可以求出二元一次方程的解，因此我们可以从前往后，两个数就可以找到一组解，这样两两合并即可得到一组合法的解。

即：先考虑 $A_1{X}_1+A_2{X}_2$，我们可以求出方程 $A_{1}x+A_{2}y=\gcd (A_1,A_2)$ 的解 $x,y$，此时 $x$ 就是满足当前条件的 $X$ 序列的第一项的解，$X_1=x,X_2=y$。我们把 $\gcd (A_1,A_2)$ 当作新的元素，于是得到新的方程：

$$\gcd (A_1,A_2)x+A_3\ast X_3+...+A_n\ast X_n+PQ=B,Q\in \mathbb{Z}$$

我们再合并 $gcd(A1,A2)$ 和 $A3$ ，解出 $\gcd (A_1,A_2)x+A_{3}y=\gcd (\gcd (A_1,A_2),A_3)$ 的 $x,y$，把之前求出的所有的 $X_i$乘上 $x$（一层一层的），$X_3=y$ ，不断重复，直到合并只剩两项为止。

最后求解 $\gcd (A_1,A_2,A_3...A_n)x+Py$ 的 $x,y$，判断 $\gcd (A_1,A_2,A_3...A_n)$ 能否整除 $B$ ，若不能整除，显然该丢番图方程无解，输出 $NO$ 即可。

若能整除，所有的解乘上 $\frac{B}{\gcd (A_1,A_2...A_n,P)}$ 即为一组合法的解，输出即可。

注意我们在求解 $x,y$ 的过程中可能得到负数解，而题目要求输出整数解，最后输出的时候将 $X_i$ 置于 $[0,P]$ 之间即可。

Code

#include 
using namespace std;
const int maxn = 100 + 7;
int n, m, s, t, k, ans;
int X[maxn];
int A[maxn], p, b;

int exgcd(int a, int b, int &x, int &y)
{
     
	if(b == 0) {
     
		x = 1, y = 0;
		return a;
	}
	int d = exgcd(b, a % b, x, y);
	int z = x;
	x = y, y = z - y * (a / b);
	return d;
}

int main()
{
     
	scanf("%d%d%d", &n, &p, &b);
	for (int i = 1; i <= n; ++ i)
		scanf("%d", &A[i]), A[i] %= p;
	int gcd = A[1]; 
	X[1] = 1;
	for (int i = 2; i <= n; ++ i) {
     
		int x, y; 
		gcd = exgcd(gcd, A[i], x, y);
		for (int j = 1; j < i; ++ j)
			X[j] = X[j] * x % p;
		X[i] = y; 
	} 
	int x, y;
	gcd = exgcd(gcd, p, x, y);
	for (int i = 1; i <= n; ++ i)
		X[i] = X[i] * x % p;
	if(b % gcd != 0) {
     
		puts("NO");
		return 0;
	}
	else {
     
		puts("YES");
		for (int i = 1; i <= n; ++ i) {
     
			X[i] = X[i] * b / gcd % p;
			printf("%d ", (X[i] + p) % p);
		}
	}
	puts("");
	return 0;
}

1.5.2 欧几里得

Problem A.Wizards

UVALive 4305

1.5.3 欧拉定理

Problem A.Strange Limit（拓展欧拉定理）

ZOJ 2674

Problem

定义数列 $a_1=p$，$a_{n+1}=p^{a_n}(n\ge 1)$

其中 $p$ 是素数，定义 $b_n=a_n\mathrm{m}\mathrm{o}\mathrm{d}m!$

要求求出：$\underset{n\to \infty }{\lim }{b}_n$

$2\le p,m\le 12$。

Solution

其实就是求 $p^{p^{p^{p^{\dots }}}}$。

拓展欧拉定理递归计算即可。

由于 $m!\le 4\times 10^8$，所以我们每次需要 $O(\sqrt{n})$ 计算 $\phi$，时间复杂度 $O(n\sqrt{n})$。

Code

#include 
using namespace std;
#define int long long
const int maxn = 1e6 + 7;
int n, m, s, t, k, ans;
int fact;
int p;

int qpow(int a, int b, int mod)
{
     
	int res = 1;
	while(b) {
     
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}

int phi(int x)
{
     
	int ans = x;
	for (int i = 2; i * i <= x; ++ i) {
     
		if (x % i == 0) {
     
			ans = ans / i * (i - 1);
			while (x % i == 0) 
				x /= i;
		}
	}
	if (x > 1)
		ans = ans / x * (x - 1);
	return ans;
}

int solve(int a, int b)
{
     
	if(b == 1) return 0;
	int phi_b = phi(b); 
	return qpow(a, phi_b + solve(a, phi_b), b);
}

signed main()
{
     
	bool flag = false;
	while(scanf("%lld%lld", &p, &m) != EOF) {
     
		if(flag) puts("");
		else flag = true;
			
		fact = 1;
		for (int i = 1; i <= m; ++ i)
			fact = fact * i;
		cout << solve(p, fact) << endl;	
	}
	return 0;
}

1.5.4 欧拉函数

Problem A.GCD Determinant（$\gcd$ 矩阵定理）

UVALive 4190

Problem

给定 $n$ 个数 $a_1,a_2,a_3\cdots ,a_n$，且对于任意 $a_i$ 的约数 $d$ ，$d$ 均在数集 $\{a_i\}$ 中，用这 $n$ 个数构造一个 $n\times n$ 的矩阵，其中第 $i$ 行第 $j$ 列的数是 $a_i$ 和 $a_j$ 的最大公约数。

求这个矩阵的行列式的值，结果模 $10^9+7$。

$0<n<1000,0<x_i<2\times 10^9$

Solution

显然矩阵中的数是一些数的因子集合。

由于行列式交换两行或者两列以后，行列式的值会变号，因此我们可以把输入的因子集合 $\{a_i\}$ 从小到大进行排序，列交换的同时，行也进行交换，因此排序后的行列式的值不变，得到一个矩阵形如：

$$\left[\begin{array}{ccccc}\gcd (a_1,a_1)& \gcd (a_1,a_2)& \gcd (a_1,a_3)& \cdots & \gcd (a_1,a_n)\\ \gcd (a_2,a_1)& \gcd (a_2,a_2)& \gcd (a_2,a_3)& \cdots & \gcd (a_2,a_n)\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ \gcd (a_n,a_1)& \gcd (a_n,a_2)& \gcd (a_n,a_3)& \cdots & \gcd (a_n,a_n)\end{array}\right]$$

其中 $a_i<a_{i+1}$。这里输入的元素 $a_i$ 是封闭的，即：若 $x$ 在 $\{a_i\}$ 中，则 $x$ 的所有因子均在 $\{a_i\}$ 中。

计算矩阵的行列式，我们将矩阵对角化，设对角化之后，对角线上的数为 $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}[i]$，显然有：

$$\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}[i]=a_i-\sum _{j=1}^{i-1}[\gcd (a_j,a_i)==a_j?\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}[i]:0]$$

其中 $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}[1]=1$。

直接递推计算，时间复杂度 $O(n^2\log a_i)$，可以通过本题。

这里有一个有趣的性质，类似本题中满足 $\mathrm{g}\mathrm{c}\mathrm{d}-\mathrm{c}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{d}$ 的 $\gcd$ 矩阵的行列式等于元素的欧拉函数的乘积：

$$\mathrm{d}\mathrm{e}\mathrm{t}=\sum _{i=1}^n\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}[i]=\sum _{i=1}^n(\phi (a_i))$$

证明：

因此我们只需要求出每个数的欧拉函数，累乘即可。

时间复杂度 $O(n\sqrt{n})$。

Code

#include 
using namespace std;
#define int long long
const int maxn = 1e3 + 7, mod = 1e9 + 7;
int n, m, s, t, k, ans;
int a[maxn];
int phi(int n)
{
     
	int ans = n;
	for (int i = 2; i * i <= n; ++ i) {
     
		if (n % i == 0) {
     
			ans = ans / i * (i - 1);
			while (n % i == 0) 
				n /= i;
		}
	}
	if (n > 1)
		ans = ans / n * (n - 1);
	return ans;
}

signed main()
{
     
	while(scanf("%lld", &n) != EOF) {
     
		ans = 1;
		for (int i = 1; i <= n; ++ i) {
     
			int x;
			scanf("%lld", &x);
			ans = ans * phi(x) % mod;
		}
		cout << ans << endl;
	}
	return 0;
}

1.5.5 平方剩余

Problem A.Square Root（二次剩余）

URAL 1132

Problem

给定一个质数 $p$ 以及正整数 $a$，求方程 $x^2\equiv a(\mathrm{m}\mathrm{o}\mathrm{d}p)$ 的所有的解。

$1\le a,p\le 2^{15}-1$，保证 $a$ ，$p$ 互质。

Solution

2008年的论文题。

当年还是一个新知识，现在就是一个板子。

套用二次剩余模板即可。

Code

#include 
#include 
#include 
using namespace std;
using ll = long long;
const int maxn = 1e5 + 7;

int mod;
ll I_mul_I; // 虚数单位的平方
struct Complex {
     //自己实现复数
	ll real, imag;
	Complex(ll real = 0, ll imag = 0): real(real), imag(imag) {
      }
};
inline bool operator == (Complex x, Complex y) {
     
	return x.real == y.real and x.imag == y.imag;
}
inline Complex operator * (Complex x, Complex y) {
     
	return Complex((x.real * y.real + I_mul_I * x.imag % mod * y.imag) % mod,
			(x.imag * y.real + x.real * y.imag) % mod);
}
Complex qpow(Complex x, int k) {
     
	Complex res = 1;
	while(k) {
     
		if(k & 1) res = res * x;
		x = x * x;
		k >>= 1;
	}
	return res;
}
bool check_if_residue(int x) {
     
	return qpow(x, (mod - 1) >> 1) == 1;
}
int solve(int n, int p) {
     
	n %= p, mod = p;
	if(p == 2) return n;
	ll a = rand() % mod;
	if(qpow(n,(mod - 1) / 2) == p - 1) return -1;//不存在
	while(!a || check_if_residue((a * a + mod - n) % mod))
		a = rand() % mod;
	I_mul_I = (a * a + mod - n) % mod;

	return int(qpow(Complex(a, 1), (mod + 1) >> 1).real);
}
int n, m, p, t;
int main()
{
     
    //srand(time(0));
    scanf("%d", &t);
    while(t -- ) {
     
        scanf("%d%d", &n, &p);
        int ans1 = 0, ans2 = 0;
        if(n == 0) {
     
            puts("0");
            continue;
        }
        ans1 = solve(n, p);
        if(ans1 == -1) puts("No root");
        else {
     
            ans2 = p - ans1;
            if(ans1 > ans2) swap(ans1, ans2);
            if(ans1 == ans2) printf("%d\n", ans1);
            else printf("%d %d\n", ans1, ans2);
        }
    }
    return 0;
}

1.5.6 原根

Problem A.Fermat’s Last Theorem

SGU 511

Problem

1.5.7 整除与剩余

Problem A.Brute-Force Algorithm（乘法换加法，矩阵快速幂）

HDU 3221

给定如下的递归函数，求输入时的 $\mathrm{f}\mathrm{u}\mathrm{n}\mathrm{n}\mathrm{y}()$ 函数被调用的次数。

输出模 $p$ 的结果。

$1\le n\le 10^9,1\le p\le 10^6,0\le a,b\le 10^6$

Solution

设 $f(i)$ 表示输入 $i$ 时，函数被调用的次数。

显然有 $f(1)=a,f(2)=b$，$f[i]=f[i-1]\times f[i-2]$。

看上去就是乘法版的斐波那契数列，显然我们可以将乘法转化为加法，即在指数下， $f(i)$ 就是一个类斐波那契数列，设 $fib(i)$ 表示斐波那契数列，则有 $f(i)=a^{fib(n-2)}\times b^{fib(n-1)}$

本题要求的是 $f(i)\mathrm{m}\mathrm{o}\mathrm{d}p=a^{fib(n-2)}\times b^{fib(n-1)}\mathrm{m}\mathrm{o}\mathrm{d}p$。

我们利用矩阵快速幂求出 $fib(n-2)$ 和 $fib(n-1)$ 之后，快速幂计算即可。

Code

不知道为啥wa了呜呜呜…

#include 
#include 
#include 
#include 
#define int long long
using namespace std;
typedef long long ll;
const int maxn = 2e6 + 7, maxm = 2;
int n, m, s, t, k, ans, kcase;
ll a, b, p;
int primes[maxn], cnt;
bool vis[maxn];
int phi[maxn];

void get_phi(int n)
{
     
	phi[1] = 1;
	for (int i = 2; i <= n; ++ i) {
     
		if (vis[i] == 0) {
     
			primes[ ++ cnt] = i;
			phi[i] = i - 1;
		}
		for (int j = 1; j <= cnt && primes[j] * i <= n; ++ j) {
     
			vis[i * primes[j]] = 1;
			if (i % primes[j] == 0) {
     
				phi[i * primes[j]] = phi[i] * primes[j];
				break;
			}
			phi[i * primes[j]] = phi[i] * (primes[j] - 1);
		}
	}
}

void mul(ll c[], ll a[], ll b[][maxm])
{
     
	ll tmp[maxm] = {
     0};
	for (int j = 0; j < maxm; ++ j) 
		for (int k = 0; k < maxm; ++ k)
			tmp[j] = (tmp[j] + a[k] * b[k][j]) % phi[p];
	memcpy(c, tmp, sizeof tmp);
}

void mul(ll c[][maxm], ll a[][maxm], ll b[][maxm])
{
     
	ll tmp[maxm][maxm] = {
     0};
	for (int i = 0; i < maxm; ++ i)
		for (int j = 0; j < maxm; ++ j)
			for (int k = 0; k < maxm; ++ k)
				tmp[i][j] = (tmp[i][j] + a[i][k] * b[k][j]) % phi[p];
	memcpy(c, tmp, sizeof tmp);
}

ll qpow(ll a, ll b, ll mod)
{
     
	ll res = 1;
	while (b) {
     
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
	
} 

ll Matqpow(ll n)
{
     
	
	ll f[maxm] = {
     0, 1};
	ll A[maxm][maxm] = {
     
		{
     0, 1}, 
		{
     1, 1},
	};
	if (n <= 2) return 1;
	while (n) {
     
		if (n & 1) mul(f, f, A);
		mul(A, A, A);
		n >>= 1;
	}
	return f[0] % phi[p];
}

signed main()
{
     
	scanf("%lld", &t);
	get_phi(maxn - 6);
	while (t -- ) {
     
		printf("Case #%lld: ",  ++ kcase); 
		scanf ("%lld%lld%lld%lld", &a, &b, &p, &n);
		if (n == 1) {
     
			printf("%lld\n", a % p);
			continue;	
		}
		else if (n == 2) {
     
			printf("%lld\n", b % p);
			continue;
		}
		else if (n == 3) {
     
			printf("%lld\n", a * b % p);
			continue;
		} 
		ll fiba = Matqpow(n - 2);
		ll fibb = Matqpow(n - 1); 
		if (fiba >= phi[p]) fiba = fiba % phi[p] + phi[p];
		if (fibb >= phi[p]) fibb = fibb % phi[p] + phi[p]; 
		ll ansa = qpow(a, fiba, p) % p;
		ll ansb = qpow(b, fibb, p) % p;
		 
		cout << ansa * ansb % p << '\n';
	}
	return 0;
} 

Problem B. Interal Roots（多项式，整数）

POJ 3471

Problem

给定一个多项式 $f(x)=x^n+a_{n-1}{x}^{n-1}+\cdots +a_0$，求 $f(x)=0$ 的所有整数解，注意，重根算作不同的根。

$n\le 100,|a_i|<2^{31}$

Solution

求所有的整数解，设一共有 $m$ 个整数解： $x_1,x_2,\cdots ,x_m$

则有 $f(x)=(x-x_1)(x-x_2)\cdots (x-x_m)g(x)$，其中 $g(x)$ 表示剩余的没有整数解的多项式。

若不存在 $g(x)$，则显然有 $\prod _{i=1}^m{x}_i=a_0$。

若存在 $g(x)$，设 $g(x)$ 的常数项为 $t$ ，则显然有 $t\times \prod _{i=1}^m{x}_i=a_0$。

则显然有： $\prod _{i=1}^m{x}_i\mid a_0$

因此我们就可以枚举 $a_0$ 的所有因子 $a^{\prime }$（注意因为多项式的整数解可能为负数，所以我们需要枚举的因子包括负数因子），判断 $(x-a^{\prime })$ 是否为 $f(x)$ 的约数，其中 $n\le 100$，我们只需要做暴力 $O(n^2)$ 的多项式除法 $\frac{f(x)}{x-a^{\prime }}=\frac{(x-x_1)(x-x_2)\cdots (x-x_m)g(x)}{x-a^{\prime }}$ 判断是否整除即可。若是 $f(x)$ 的约数，显然 $a^{\prime }$ 是 $f(x)$ 的一个整数解。或者直接带入 $x=a^{\prime }$，计算多项式的值看是否为 $0$ 即可。

若 $a_0=0$，我们只需要将多项式 $f(x)$ 除掉一个 $x$， 直到 $a_0\ne 0$ 为止即可。注意此时 $a_0=0$ 说明有一个整数解 $0$。

注意计算重根即可。

时间复杂度 $\mathcal{O}(n\sqrt{a_i})$。

Code

#include 
#include 
#include 
#include 
#include 
using namespace std;
const long long maxn = 1e2 + 6, maxm = 1e5 + 7;

long long n, m, s, t, k, ans[maxm], kcase;
long long tot;
long long a[maxn];

void get(long long k)
{
     
	long long tmp[maxn];
	tmp[0] = a[0];
	while(n) {
     
		for (int i = 1; i <= n; ++ i)
			tmp[i] = a[i], a[i] = a[i - 1] * k + a[i];
		if (a[n]) {
     
			for (int i = 0; i <= n; ++ i)
				a[i] = tmp[i];
			break;
		}
		ans[ ++ tot] = k, n -- ;
	}
}

void solve()
{
     
	a[0] = 1;
	// cin >> a[n - 1], a[n - 2], ..., a[2], a[1], a[0];
	for (int i = 1; i <= n; ++ i)
		scanf("%lld", &a[i]);
	tot = 0;
	//a_0 = 0 ，多项式除 x 直到 a_0 != 0
	while(n && a[n] == 0) 
		ans[ ++ tot] = 0, n -- ;
	long long a_0 = a[n] < 0 ? -a[n] : a[n];
	int len = int(sqrt(a_0 + 0.5));
	for (int i = 1; i <= len; ++ i) {
     
		if (a_0 % i == 0) {
     
			get(i), get(-i);
			get(a_0 / i), get(-a_0 / i);
		}
	}
	cout << tot << endl;
	sort(ans + 1, ans + 1 + tot);
	for (int i = 1; i <= tot; ++ i)
		printf("%lld\n", ans[i]); 
}

int main()
{
     
	while(scanf("%lld", &n) != EOF) {
     
		solve();
	}
	return 0;
}

Problem C.Vivian’s Problem（梅森素数，状压DP）

ZOJ 2360

给定 $k$ 个整数 $q_1,q_2,\cdots ,q_k$，求一个具有如下形式的 $N$：

$$N=\prod _{i=1}^k{q}_i^{c_i}(0\le c_i\le 10,\sum _{i=1}^k{c}_i\ge 1,1\le i\le k)$$

其中 $c_i$ 由你任意地制定，记 $M$ 为 $N$ 的所有约数的和，问是否存在一个 $N$ ，使得 $M$ 恰好是 $2$ 的幂。如果没有这样的 $N$ 存在，输出 NO。若 $M=2^x$，则输出 $x$；若有多个 $x$ ，输出其中最大的一个。

$1\le k\le 100,1<q_i<2^{31}$

Solution

首先对于一个数 $N$，由唯一分解定理可得 $N=p_1^{a_1}{p}_2^{a_2}\cdots p_r^{a_r}$

显然有约数和 $M=(1+p_1+p_1^2+p_1^3+\cdots +p_1^{a_1})\times \cdots \times (1+p_r+p_r^2+p_r^3+\cdots +p_r^{a_r})$

要求 $M=2^x$，显然该连乘式中每个括号内的 $(1+p_i+p_i^2+p_i^3+\cdots +p_i^{a_i})$ 均为 $2$ 的幂。

由于 $p$ 是质数，显然当 $p=2$ 时，$(1+p_i+p_i^2+p_i^3+\cdots +p_i^{a_i})=1+2\times (\cdots )\ne 2^x$。

则 $p$ 均为奇数，显然括号内必然有偶数项，否则和一定是奇数。

则有

$$\begin{array}{rlr}& 1+p_i+p_i^2+p_i^3+\cdots +p_i^{a_i}& \\ & =(1+p_i^2+p_i^4+\cdots +p_i^{a_{i-1}})+(p_i+p_i^3+p_i^5+\cdots +p_i^{a_i})& \\ & =(1+p)(1+p_i^2+p_i^4+\cdots +p_i^{a_{i-1}})& \end{array}$$

显然这两个括号内都是偶数项，则有：

$$\begin{array}{rlr}& (1+p)(1+p_i^2+p_i^4+\cdots +p_i^{a_{i-1}})& \\ & =(1+p)(1+p_i^4+p_i^8\cdots +p_i^{a_{i-3}})+(p_i^2+p_i^6+p_i^{10}+\cdots +p_i^{a_i-1})& \\ & =(1+p)(1+p^2)(1+p_i^4+p_i^8\cdots +p_i^{a_{i-3}})& \end{array}$$

若 $(1+p)$ 和 $(1+p^2)$ 均为 $2$ 的幂，显然有 $(1+p)<(1+p^2)\Rightarrow (1+p)\mid (1+p^2)$

$(1+p^2)=(p^2-1)+2=(p+1)(p-1)+2$

若 $(1+p)\mid (1+p^2)$，则 $(1+p)\mid (p-1),(1+p)\mid 2\Rightarrow p=1$

$1$ 显然不是质数，显然 $(1+p)$ 和 $(1+p^2)$ 不可能为 $2$ 的幂，因此 $\forall i,a_i=1$。

因此所有合法的 $N$，一定是若干 $p$ 的一次方的乘积，且 $(1+p)$ 是 $2$ 的幂，$p<2^{31}$，合法的 $p$ 显然非常少，只有 $8$ 个，我们可以直接暴力 $O(\log p)$ 找到这 $8$ 个数。

问题就变成了，给定 $n$ 个数 $q_i$，求从这 $n$ 个数中选出若干个数，乘积 $N$ 仅有这 $8$ 个 $p$ 组成，且不能有重复，如何选取 $q_i$ 使得它们的约数和 $M$ 最大。

我们可以预处理出所有可能的 $N$ ，对于每个输入的 $q_i$，使用二进制数表示它包含这 $8$ 个数里的那几个，这样 & 起来为 $0$ 说明没有重复。我们就可以直接进行状压DP，$f[i]$ 表示 $i$ 能否在合法的前提下被凑出来，时间复杂度 $O(2^8\times n)$。

Code

#include 
using namespace std;
using ll = long long;
const int maxn = 1e3 + 7, maxp = 10 + 7;
int n, m, s, t, k, ans;
int p[maxp], pow_num[maxp], tot;
int q[maxn];
int f[maxn];

void init()
{
     
	ll x = 4;
	int cnt = 2; 
	while (x < (1ll << 31) + 1) {
     
		ll y = x - 1; 
		bool flag = 1;
		for (ll i = 2; i * i <= y; ++ i) {
     
			if (y % i == 0) {
     
				flag = 0;
				break;
			}
		}
		if(flag) p[tot] = y, pow_num[tot ++ ] = cnt;
		x <<= 1; 
		cnt ++ ;
	} 
}

int check(int x)
{
     
	int cnt = 0;
	for (int i = 0; i < tot; ++ i) {
     
		if(x % p[i] == 0) {
     
			cnt |= (1 << i);
			x /= p[i];
		} 
	} 
	if(x > 1) return 0;
	return cnt;
}

int cal(int x)
{
     
	int res = 0;
	for (int i = 0; i < tot; ++ i) {
     
		if(x & (1 << i))
			res += pow_num[i];
	}
	return res;
}

int main()
{
     
	init();	
	while(scanf("%d", &n) != EOF) {
     
		memset(f, 0, sizeof f);
		for (int i = 1; i <= n; ++ i) {
     
			int x;
			scanf("%d", &x);
			q[i] = check(x); 
			if(q[i] == 0)
				i -- , n -- ;
		}	
		if(n == 0) {
     
			puts("NO");
			continue;
		}		
		f[0] = 1;
		int ans = 0;
		for (int i = 1; i <= n; ++ i) 
			for (int j = 0; j < (1 << tot); ++ j) 
				if((j & q[i]) == 0) //没有重复
					f[j | q[i]] |= f[j];
		for (int i = 0; i < (1 << tot); ++ i)
			if(f[i])
				ans = max(ans, cal(i));
		cout << ans << endl;
	}
	return 0;
}

其中题目中的素数 $p$ 实际上就是梅森素数：

1.5.8 中国剩余定理

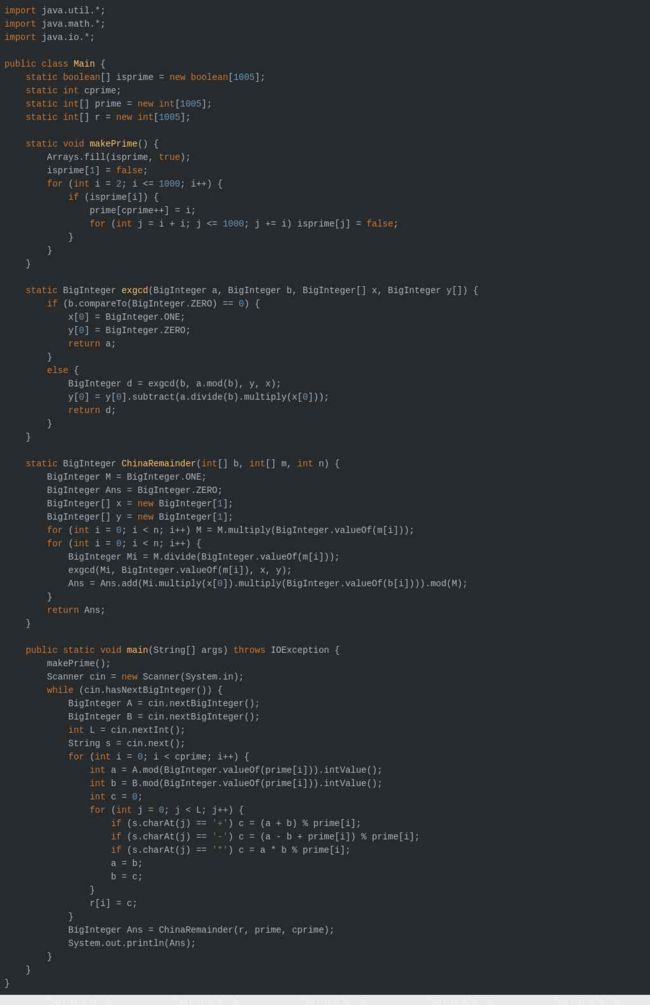
Problem A.Voyager 1（Java高精，中国剩余定理）

ZOJ 3341

给定两个整数 $A_{-1}$ 和 $A_0$，以及一个长度为 $L$ 的操作串 $Op$（仅包括加减乘）。对于 $1\le i\le L,A_i=A_{i-2}O{p}_i{A}_{i-1}$（对 $A_{i-2}$ 和 $A_{i-1}$ 进行 $Op+i$ 操作），求 $A_L$。

所有操作均在模 $M$ 的意义下进行，其中 $M$ 为小于 $1000$ 的所有质数的乘积。

$1\le L\le 3\times 10^5$

Solution

显然 $M$ 是一个非常非常大的数， $1000!$ 级别的数，直接进行高精度计算显然会爆炸超时。

但是给定的 $M$ 为小于 $1000$ 的所有质数的乘积，显然我们可以分别求出在模这些质数下的结果，然后中国剩余定理合并即可…

数据还是很大， 需要使用大数…所以Java yyds

Code

1.6 分析

Problem A.Bridge

ZOJ 2614