【机器学习实践】使用Python实现k-均值聚类算法、DBSCAN算法和AGNES算法
前言
本周学习了周志华《机器学习》第9章聚类，本章主要介绍了三种类型的聚类算法：原型聚类、密度聚类和层次聚类。介绍的原型聚类中，有k-均值聚类、学习向量量化和高斯混合聚类。而密度聚类和层次聚类分别有有DBSCAN算法和AGNES算法。为了加强对算法实现过程的理解和加强练习Python代码能力，于是使用Python分别实现了三种类型聚类算法中的各自比较著名的k-均值聚类算法、DBSCAN算法和AGNES算法。
学习笔记
K均值算法：求最小化平方误差的最优解是NP难问题，因此k均值算法采用贪心策略通过迭代优化来近似求解。基本步骤如下：
- 1、假设样本集为
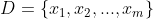，聚类簇数为k，则先随机从样本集中选出k个样本作为均值向量
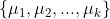; - 2、计算每个样本
与各均值向量的距离，选择离 距离最小的一个均值向量，将 划入该均值向量对应的簇中; - 3、所以样本划分完成后，计算每个簇的均值向量
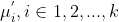; - 4、将簇的均值向量更新为
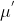，迭代执行第2和第3步，直至均值向量不再发生变化。
学习向量量化：与k均值算法类似，但是它的样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。基本步骤如下：
- 1、假设样本集为
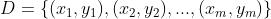，设置原型向量个数为q，各原型向量预设的类别标记为
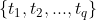，学习率为η，初始化原型向量p; - 2、从样本集D中随机选取样本
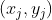，计算与 距离最近的原型向量
，如果
与 对应的类别标记
一致，则将 更新为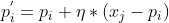 
，否则更新为 
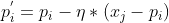; - 3、迭代执行达到一定次数后得到的一组原型向量p，即可实现对样本进行聚类。
高斯混合聚类：采用概率模型来表达聚类原型，实现过程使用EM算法获得高斯混合模型。基本步骤如下：
- 1、假设样本集为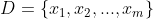，高斯混合成分个数为k，初始化高斯混合分布模型参数
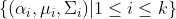； - 2、计算由
各混合成分生成的后验概率，即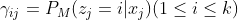
; - 3、根据后仰概率计算新的均值向量
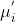、新协方差矩阵
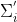和新混合系数
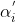，将参数原来的值更新为新的值； - 4、迭代执行第2、第3步，直至达到一定迭代次数
- 5、根据最后得出的高斯混合分布模型参数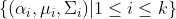可以将样本分类成k个簇。
DBSCAN算法：是一种著名的密度聚类算法，它基于一组“领域”参数来刻画样本分布的紧密程度。基本步骤如下：
- 1、假设样本集为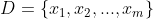，设定领域参数
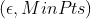，找出所以核心对象，生成核心对象集合Ω，记录未访问对象集合
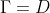； - 2、使用
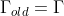记录开始时未访问的对象，初始化聚类簇数k=0； - 3、随机选择一个核心对象o，初始化队列Q=
取出队列中的首个元素，若该元素是核心对象，则将其领域且和的交集的点集Δ全部入队Q，更新 Δ，迭代执行直至队列Q为空；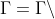
- 4、则生成的一个簇
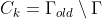，更新参数k=k+1，Ω = Ω 
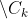； - 5、迭代执行直至Ω为空集，最后将得到k个簇
。
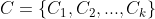AGNES算法：是一种采用自底向上聚合策略的层次聚类算法，基本步骤如下：
- 1、假设样本集为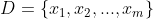，聚类簇数为k，先将每个样本看成是一个簇，则开始时具有m个簇；
- 2、计算每个簇与簇之间的距离，每次合并距离最小的两个簇；
- 3、迭代执行第2步，直至剩余的簇数等于k个；
- 4、最后剩余的k个簇就是聚类结果。
算法代码和运行结果
k-均值聚类
import numpy as np
import random
import math
import copy
import matplotlib.colors as cl
import matplotlib.pyplot as plt
#西瓜数据集4.0
def loadDataSet():
dataSet = [[0.697, 0.460],
[0.774, 0.376],
[0.634, 0.264],
[0.608, 0.318],
[0.556, 0.215],
[0.403, 0.237],
[0.481, 0.149],
[0.437, 0.211],
[0.666, 0.091],
[0.243, 0.267],
[0.245, 0.057],
[0.343, 0.099],
[0.639, 0.161],
[0.657, 0.198],
[0.360, 0.370],
[0.593, 0.042],
[0.719, 0.103],
[0.359, 0.188],
[0.339, 0.241],
[0.282, 0.257],
[0.748, 0.232],
[0.714, 0.346],
[0.483, 0.312],
[0.478, 0.437],
[0.525, 0.369],
[0.751, 0.489],
[0.532, 0.472],
[0.473, 0.376],
[0.725, 0.445],
[0.446, 0.459]]
return dataSet
#计算样本和均值向量的距离
def getDist(x, ui, p = 2):
x = np.array(x)
ui = np.array(ui)
temp = abs(x - ui) ** p
minkov_dist = math.sqrt(sum(temp))
return minkov_dist
#初始化均值向量，从样本集中随机选择k个
def init(dataSet, k):
u = random.sample(dataSet, k)
return u
#随机生成簇显示的颜色集
def generateColors(k):
colorSet = []
cname = list(cl.cnames.keys()) #color库中的颜色字典的key
colorSet = random.sample(cname, k ) #随机选择k个
colorSet.append('red') #均值向量使用红色显示
return colorSet
#根据簇绘制散点图
def drawScatter(clusters, colors, count, u):
k = len(clusters)
fig = plt.figure()
label_Com = ['mean_Points'] #散点标签
u_x = [example[0] for example in u]
u_y = [example[1] for example in u]
#显示均值向量
plt.scatter(u_x, u_y, c= colors[-1], marker = u'+', s = 100)
#显示各个簇
for i in range(k):
x = [example[0] for example in clusters[i]]
y = [example[1] for example in clusters[i]]
plt.scatter(x, y, c=colors[i])
label_Com.append('cluster{num}'.format(num = i))
ax = fig.gca()
plt.xlabel('Density')
plt.ylabel('Sugar')
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles, labels = label_Com, loc = 'upper left')
plt.grid(True)
plt.title('{num} times clustering result'.format(num = count))
plt.show()
#k-means聚类
def k_means(dataSet, k):
u = np.array(init(dataSet, k)) #初始化均值向量
# u = np.array([[0.403, 0.237],
# [0.343, 0.099],
# [0.478, 0.437]])
u_old = np.zeros([k, len(dataSet[0])]) #记录某次迭代之前的均值向量
count = 0 #记录迭代次数
colors = generateColors(k) #生成显示簇的颜色集
while (u != u_old).any() and count < 10: #当均值向量与更新之前的值不相同
#或迭代次数少于10都将继续迭代
u_old = copy.deepcopy(u)
clusters = [[] for col in range(k)] #记录每个簇的数据
for x in dataSet:
min_dist = -1 #记录最小距离的值
bestIndex = -1 #记录距离样本最小的均值向量下标
for j in range(k):
dist = getDist(x, u[j])
if min_dist == -1 or dist < min_dist:
min_dist = dist
bestIndex = j
clusters[bestIndex].append(x) #将该样本划入此均值向量对应的簇里面
for i in range(k): #更新均值向量的值
c = np.array(clusters[i])
u[i] = np.mean(c, axis = 0)
count += 1
drawScatter(clusters, colors, count, u) #绘制散点图
#测试代码
dataSet = loadDataSet()
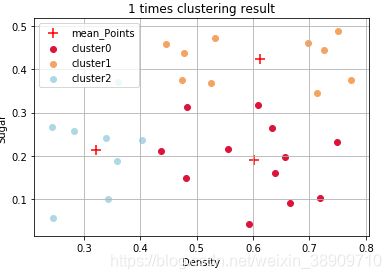
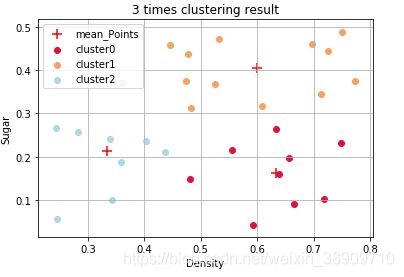
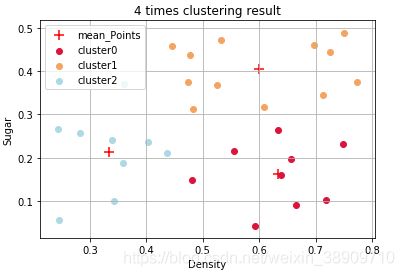
k_means(dataSet, 3) 运行结果
以下4图分别为第1次到第4次迭代后的分类结果，第4次迭代后更新后的均值向量与之前没有变化，所以迭代结束。由于初始化时的均值向量不同，每次运行的迭代次数不尽相同。
DBSCAN聚类
import numpy as np
import random
import math
import copy
import queue
import matplotlib.colors as cl
import matplotlib.pyplot as plt
#载入西瓜数据集4.0
def loadDataSet():
dataSet = [[0.697, 0.460],
[0.774, 0.376],
[0.634, 0.264],
[0.608, 0.318],
[0.556, 0.215],
[0.403, 0.237],
[0.481, 0.149],
[0.437, 0.211],
[0.666, 0.091],
[0.243, 0.267],
[0.245, 0.057],
[0.343, 0.099],
[0.639, 0.161],
[0.657, 0.198],
[0.360, 0.370],
[0.593, 0.042],
[0.719, 0.103],
[0.359, 0.188],
[0.339, 0.241],
[0.282, 0.257],
[0.748, 0.232],
[0.714, 0.346],
[0.483, 0.312],
[0.478, 0.437],
[0.525, 0.369],
[0.751, 0.489],
[0.532, 0.472],
[0.473, 0.376],
[0.725, 0.445],
[0.446, 0.459]]
return dataSet
#计算两样本间的距离
def getDist(x, y, p = 2):
x = np.array(x)
y = np.array(y)
temp = abs(x - y) ** p
minkov_dist = math.sqrt(sum(temp))
return minkov_dist
#寻找核心对象及其领域、邻域的点集
def searchCore(dataSet, R, MinPts):
dataLength = len(dataSet)
domainDict= {} #记录所有核心对象的邻域点集的字典
cores = [] #记录核心对象
for i in range(dataLength):
domain = [] #记录某个核心对象的领域点
for j in range(dataLength):
dist = getDist(dataSet[i], dataSet[j], 2)
if dist <= R:
domain.append(dataSet[j])
if len(domain) >= MinPts:
cores.append(dataSet[i])
domainDict[i] = domain
return cores, domainDict
#根据簇的分类结果和原始数据集找出噪声点，用于观察分类效果
#（即是求原数据集与所有簇的差集）
def findNoiseData(clusters, dataSet):
cp_cluster = [data for elem in clusters for data in elem]
noise_point = []
for x in dataSet:
if x not in cp_cluster:
noise_point.append(x)
return noise_point
#绘制各个簇和噪声点的散点图
def drawScatter(clusters, noise):
k = len(clusters) #簇的个数
cname = list(cl.cnames.keys()) #颜色集
colors = random.sample(cname, k) #随机选取K个颜色集
fig = plt.figure()
label_Com = ['Noise sample'] #散点标签集
#显示噪声点
u_x = [example[0] for example in noise]
u_y = [example[1] for example in noise]
plt.scatter(u_x, u_y, c= u'gray', marker = u'*', s = 80)
#显示各个簇
for i in range(k):
x = [example[0] for example in clusters[i]]
y = [example[1] for example in clusters[i]]
plt.scatter(x, y, c=colors[i])
label_Com.append('cluster{num}'.format(num = i))
ax = fig.gca()
plt.xlabel('Density')
plt.ylabel('Sugar')
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles, labels = label_Com, loc = 'upper left')
plt.grid(True)
plt.title('DBSCAN clustering')
plt.show()
#DBSCAN聚类
def DBSCAN_cluster(dataSet, R, MinPts):
cores, domainSet = searchCore(dataSet, R, MinPts)
k = 0 #记录簇的个数
remDataSet = copy.deepcopy(dataSet) #记录未被访问的数据集
clusters = [] #记录分类后各簇的数据
while len(cores) != 0:
oldDataSet = copy.deepcopy(remDataSet) #记录某次迭代前未被访问的数据集
rand_core = cores[np.random.randint(len(cores))] #随机选择一核心对象
q = queue.Queue()
q.put(rand_core) #将选中的核心对象入队
remDataSet.remove(rand_core) #将选中的核心对象标记为已访问
while not q.empty():
data = q.get()
if data in cores:
core_index = dataSet.index(data) #获取核心对象对应的下标
domain = domainSet[core_index] #获取此核心对象的邻域点集
for x in domain: #更新未被访问的数据集
if x in remDataSet:
q.put(x)
remDataSet.remove(x)
k = k + 1
Ck = [] #记录一个簇内的数据
for x in oldDataSet:
if x not in remDataSet:
Ck.append(x)
if x in cores:
cores.remove(x) #将已访问的核心对象删去
clusters.append(Ck)
noise = findNoiseData(clusters, dataSet) #获取噪声点，用于显示
drawScatter(clusters, noise) #绘制散点图
#测试代码
dataSet = loadDataSet()
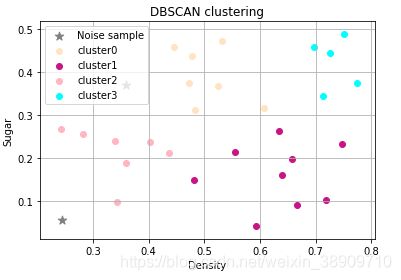
DBSCAN_cluster(dataSet, 0.11, 5) 运行结果
运行结果如下，可见DBSCAN无需确定k值，会自动根据样本确定k值，而且会自动过滤噪声样本，但是需要确定邻域参数。
AGNES聚类
import numpy as np
import random
import math
import matplotlib.colors as cl
import matplotlib.pyplot as plt
#载入西瓜数据集4.0
def loadDataSet():
dataSet = [[0.697, 0.460],
[0.774, 0.376],
[0.634, 0.264],
[0.608, 0.318],
[0.556, 0.215],
[0.403, 0.237],
[0.481, 0.149],
[0.437, 0.211],
[0.666, 0.091],
[0.243, 0.267],
[0.245, 0.057],
[0.343, 0.099],
[0.639, 0.161],
[0.657, 0.198],
[0.360, 0.370],
[0.593, 0.042],
[0.719, 0.103],
[0.359, 0.188],
[0.339, 0.241],
[0.282, 0.257],
[0.748, 0.232],
[0.714, 0.346],
[0.483, 0.312],
[0.478, 0.437],
[0.525, 0.369],
[0.751, 0.489],
[0.532, 0.472],
[0.473, 0.376],
[0.725, 0.445],
[0.446, 0.459]]
return dataSet
#计算两个簇之间的距离，根据tp的值返回距离的类型
def getDist(Ci, Cj, tp = 'max'):
length1 = len(Ci)
length2 = len(Cj)
distSum = 0
maxDist = 0
minDist = 0
for i in range(length1):
distSum_j = 0
x = np.array(Ci[i])
for j in range(length2):
y = np.array(Cj[j])
temp = abs(x - y) ** 2
minkov_dist = math.sqrt(sum(temp))
if minkov_dist > maxDist:
maxDist = minkov_dist
if minkov_dist < minDist or minDist == -1:
minDist = minkov_dist
distSum_j += minkov_dist
distSum += distSum_j
avg_dist = distSum / (length1 * length2)
if tp == 'max':
return maxDist
elif tp == 'min':
return minDist
else:
return avg_dist
#初始化距离矩阵和簇
def init(dataSet):
length = len(dataSet)
clusters = [] #记录各个簇的元素
for x in dataSet:
clusters.append([x])
#构建距离矩阵
distMat = np.zeros([length, length])
for i in range(length-1):
for j in range(i+1, length):
dist = getDist([dataSet[i]], [dataSet[j]], 'max')
distMat[i][j] = dist
distMat += distMat.T
return clusters, distMat #返回初始化的簇和距离矩阵
#找出距离矩阵的最小值对应的下标
def searchMinDist(distMat):
Mindist = -1
index = np.array([-1, -1])
length = len(distMat)
for i in range(length-1):
for j in range(i+1, length):
if Mindist == -1 or distMat[i][j] < Mindist:
Mindist = distMat[i][j]
index[0] = i
index[1] = j
return index
#根据下标合并两个簇的元素
def updateClusters(clusters, index):
clusters[index[0]].extend(clusters[index[1]])
del(clusters[index[1]])
return clusters
#更新距离矩阵
def updateDistMat(distMat, clusters, index):
#删除j行j列
distMat = np.delete(distMat, index[1], axis = 0)
distMat = np.delete(distMat, index[1], axis = 1)
length = len(distMat)
#更新合并簇后的距离矩阵
for j in range(length):
if j != index[0]:
dist = getDist(clusters[index[0]], clusters[j], 'max')
distMat[index[0]][j] = dist
distMat[j][index[0]] = dist
return distMat
#绘制散点图
def drawScatter(clusters):
k = len(clusters)
cname = list(cl.cnames.keys()) #颜色集
colors = random.sample(cname, k) #随机选取K个颜色集
fig = plt.figure()
label_Com = []
#显示各个簇
for i in range(k):
x = [example[0] for example in clusters[i]]
y = [example[1] for example in clusters[i]]
plt.scatter(x, y, c=colors[i])
label_Com.append('cluster{num}'.format(num = i))
ax = fig.gca()
plt.xlabel('Density')
plt.ylabel('Sugar')
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles, labels = label_Com, loc = 'upper left')
plt.grid(True)
plt.title('AGNES clustering Result')
plt.show()
#AGNES聚类
def AGNEScluster(dataSet, k):
clusters, distMat = init(dataSet)
while len(clusters) > k:
index = searchMinDist(distMat)
print(index)
clusters = updateClusters(clusters, index)
distMat = updateDistMat(distMat, clusters, index)
drawScatter(clusters)
#测试代码
dataSet = loadDataSet()
AGNEScluster(dataSet, 4)运行结果
运行结果如下，从原理上对比，AGNES是三者中最简单的。分类结果和DBSCAN相差不大，但是无法过滤噪声点，而且当样本较大时，效率比较低。
