Pytorch学习笔记

---

数据操作

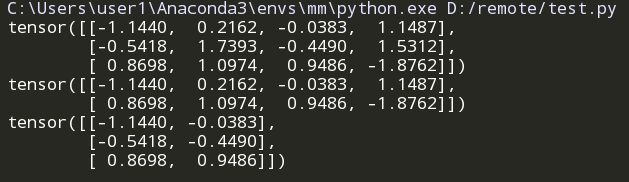
index_select(input,dim,index)

在指定dim上选取，比如选取某些行，某些列

x = torch.randn(3, 4)
print(x)

indices = torch.LongTensor([0, 2])
y = torch.index_select(x, 0, indices)
print(y)

z = torch.index_select(x, 1, indices)
print(z)

masked_select(input,mask)

a[a>0],使用ByteTensor进行选取 mask矩阵tensor必须转化为ByteTensor

import torch
a = torch.Tensor([[4,5,7], [3,9,8],[2,3,4]])
b = torch.Tensor([[1,1,0], [0,0,1],[1,0,1]]).type(torch.ByteTensor)
c = torch.masked_select(a,b)
print(c)

nonzero(input)

非0元素的下标

import torch
#a = torch.Tensor([[4,5,7], [3,9,8],[2,3,4]])
b = torch.Tensor([[1,1,0], [0,0,1],[1,0,1]])
c = torch.nonzero(b)
print(c)

gather(input,dim,index)

根据index，在dim维度上选取数据，输出的size和index一样

import torch
b = torch.Tensor([[1,2,3],[4,5,6]])
print (b)
index_1 = torch.LongTensor([[0,1],[2,0]])
index_2 = torch.LongTensor([[0,1,1],[0,0,0]])
print (torch.gather(b, dim=1, index=index_1))
print (torch.gather(b, dim=0, index=index_2))

不同于index_select是用来选择行或者列，gather是用来选择index对应的单个元素。此外输出的size和index的size一致，比如例子中的index1是22，输出也是22
index中的数字对应的是行还是列则是由dim决定，例子1中，dim=1，则index中的数字对应的将是列号，第0行（因为输出形状一致，可以确定行数）第0列是1，输出的第一个元素也就是1，第0行第1列是2，输出就是2，第一行第2列是6，输出就是6，第一行第0列是4，输出就是4。
例子2同理，第0行第0列是1，第1行第1列是5，第1行第2列是6，第0行第0列是1，第0行第1列是2，第0行第2列是3。
gather在one-hot为输出的多分类问题中，可以把最大值坐标作为index传进去，然后提取到每一行的正确预测结果，这也是gather可能的一个作用。
例子
为了得到标签的预测概率，我们可以使用gather函数。在下面的例子中，变量y_hat是2个样本在3个类别的预测概率，变量y是这2个样本的标签类别。通过使用gather函数，我们得到了2个样本的标签的预测概率。与3.4节（softmax回归）数学表述中标签类别离散值从1开始逐一递增不同，在代码中，标签类别的离散值是从0开始逐一递增的。

y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y = torch.LongTensor([0, 2])
y_hat.gather(1, y.view(-1, 1))

tensor([[0.1000],
[0.5000]])

view() 改变张量的形状

y = x.view(15)
z = x.view(-1, 5)  # -1所指的维度可以根据其他维度的值推出来
print(x.size(), y.size(), z.size())

torch.Size([5, 3]) torch.Size([15]) torch.Size([3, 5])
注意view()返回的新Tensor与源Tensor虽然可能有不同的size，但是是共享data的，也即更改其中的一个，另外一个也会跟着改变。(顾名思义，view仅仅是改变了对这个张量的观察角度，内部数据并未改变)

所以如果我们想返回一个真正新的副本（即不共享data内存）该怎么办呢？Pytorch还提供了一个reshape()可以改变形状，**但是此函数并不能保证返回的是其拷贝，所以不推荐使用。**推荐先用clone创造一个副本然后再使用view。参考此处

x_cp = x.clone().view(15)
x -= 1
print(x)
print(x_cp)

tensor([[ 0.6035,  0.8110, -0.0451],
        [ 0.8797,  1.0482, -0.0445],
        [-0.7229,  2.8663, -0.5655],
        [ 0.1604, -0.0254,  1.0739],
        [ 2.2628, -0.9175, -0.2251]])
tensor([1.6035, 1.8110, 0.9549, 1.8797, 2.0482, 0.9555, 0.2771, 3.8663, 0.4345,
        1.1604, 0.9746, 2.0739, 3.2628, 0.0825, 0.7749])

使用clone还有一个好处是会被记录在计算图中，即梯度回传到副本时也会传到源Tensor。

item()

把一个标量Tensor转化成一个Python number

x = torch.randn(1)
print(x)
print(x.item())

tensor([2.3466])
2.3466382026672363

内存开销

索引操作是不会开辟新内存的，而像y = x + y这样的运算是会新开内存的，然后将y指向新内存。

x = torch.tensor([1, 2])
y = torch.tensor([3, 4])
id_before = id(y)
y = y + x
print(id(y) == id_before) # False

如果想指定结果到原来的y的内存，我们可以使用前面介绍的索引来进行替换操作。在下面的例子中，我们把x + y的结果通过[:]写进y对应的内存中。

x = torch.tensor([1, 2])
y = torch.tensor([3, 4])
id_before = id(y)
y[:] = y + x
print(id(y) == id_before) # True

我们还可以使用运算符全名函数中的out参数或者自加运算符+=(也即add_())达到上述效果，例如torch.add(x, y, out=y)和y += x(y.add_(x))。

x = torch.tensor([1, 2])
y = torch.tensor([3, 4])
id_before = id(y)
torch.add(x, y, out=y) # y += x, y.add_(x)
print(id(y) == id_before) # True

注：虽然view返回的Tensor与源Tensor是共享data的，但是依然是一个新的Tensor（因为Tensor除了包含data外还有一些其他属性），二者id（内存地址）并不一致。

Tensor,Numpy互转

a = torch.ones(5)
b = a.numpy()
print(a, b)
-----------------------
a = np.ones(5)
b = torch.from_numpy(a)

此外上面提到还有一个常用的方法就是直接用torch.tensor()将NumPy数组转换成Tensor，需要注意的是该方法总是会进行数据拷贝，返回的Tensor和原来的数据不再共享内存。

Tensor 放到GPU上

用方法to()可以将Tensor在CPU和GPU（需要硬件支持）之间相互移动。

# 以下代码只有在PyTorch GPU版本上才会执行
if torch.cuda.is_available():
    device = torch.device("cuda")          # GPU
    y = torch.ones_like(x, device=device)  # 直接创建一个在GPU上的Tensor
    x = x.to(device)                       # 等价于 .to("cuda")
    z = x + y
    print(z)
    print(z.to("cpu", torch.double))       # to()还可以同时更改数据类型

自动求梯度

requires_grad

将其属性.requires_grad设置为True，它将开始追踪(track)在其上的所有操作（这样就可以利用链式法则进行梯度传播了）。完成计算后，可以调用.backward()来完成所有梯度计算。此Tensor的梯度将累积到.grad属性中。

如果不想要被继续追踪，可以调用.detach()将其从追踪记录中分离出来，这样就可以防止将来的计算被追踪，这样梯度就传不过去了。此外，还可以用with torch.no_grad()将不想被追踪的操作代码块包裹起来，这种方法在评估模型的时候很常用，因为在评估模型时，我们并不需要计算可训练参数（requires_grad=True）的梯度。

x = torch.ones(2, 2, requires_grad=True)
print(x)
print(x.grad_fn)

输出

tensor([[1., 1.],
        [1., 1.]], requires_grad=True)
None

再做一下运算操作：

y = x + 2
print(y)
print(y.grad_fn)

输出：

tensor([[3., 3.],
        [3., 3.]], grad_fn=)

unction是另外一个很重要的类。Tensor和Function互相结合就可以构建一个记录有整个计算过程的有向无环图（DAG）。每个Tensor都有一个.grad_fn属性，该属性即创建该Tensor的Function, 就是说该Tensor是不是通过某些运算得到的，若是，则grad_fn返回一个与这些运算相关的对象，否则是None。

注意x是直接创建的，所以它没有grad_fn, 而y是通过一个加法操作创建的，所以它有一个为的grad_fn。

像x这种直接创建的称为叶子节点，叶子节点对应的grad_fn是None。

梯度

因为out是一个标量，所以调用backward()时不需要指定求导变量：

out.backward() # 等价于 out.backward(torch.tensor(1.))

求out关于x的梯度$\frac{d(out)}{dx}$:
输出

tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])

我们令out为 $o$ , 因为 $$o=\frac{1}{4}\sum _{i=1}^4{z}_i=\frac{1}{4}\sum _{i=1}^{4}3(x_i+2{)}^2$$ 所以 $$\frac{\partial o}{\partial x_i}{|}_{x_i=1}=\frac{9}{2}=4.5$$ 所以上面的输出是正确的。
数学上，如果有一个函数值和自变量都为向量的函数 $y=f(x)$, 那么 $y$ 关于 $x$ 的梯度就是一个雅可比矩阵（Jacobian matrix）: $$J=\left(\begin{array}{ccccccc}\frac{\partial y_1}{\partial x_1}& \cdots & \frac{\partial y_1}{\partial x_n}⋮& \ddots & ⋮\frac{\partial y_m}{\partial x_1}& \cdots & \frac{\partial y_m}{\partial x_n}\end{array}\right)$$ 而torch.autograd这个包就是用来计算一些雅克比矩阵的乘积的。例如，如果 $v$ 是一个标量函数的 $l=g\left(y\right)$ 的梯度： $$v=\left(\begin{array}{ccc}\frac{\partial l}{\partial y_1}& \cdots & \frac{\partial l}{\partial y_m}\end{array}\right)$$ 那么根据链式法则我们有 $l$ 关于 $x$ 的雅克比矩阵就为: $$vJ=\left(\begin{array}{ccc}\frac{\partial l}{\partial y_1}& \cdots & \frac{\partial l}{\partial y_m}\end{array}\right)\left(\begin{array}{ccccccc}\frac{\partial y_1}{\partial x_1}& \cdots & \frac{\partial y_1}{\partial x_n}⋮& \ddots & ⋮\frac{\partial y_m}{\partial x_1}& \cdots & \frac{\partial y_m}{\partial x_n}\end{array}\right)=\left(\begin{array}{ccc}\frac{\partial l}{\partial x_1}& \cdots & \frac{\partial l}{\partial x_n}\end{array}\right)$$

注意：grad在反向传播过程中是累加的(accumulated)，这意味着每一次运行反向传播，梯度都会累加之前的梯度，所以一般在反向传播之前需把梯度清零。

# 再来反向传播一次，注意grad是累加的
out2 = x.sum()
out2.backward()
print(x.grad)

out3 = x.sum()
x.grad.data.zero_()
out3.backward()
print(x.grad)

实战

线性回归

数据输入

import torch.utils.data as Data

batch_size = 10
# 将训练数据的特征和标签组合
dataset = Data.TensorDataset(features, labels)
# 随机读取小批量
data_iter = Data.DataLoader(dataset, batch_size, shuffle=True)

定义模型

nn.Module

class Lnet(nn.Module):#一定要继承nn.Module
	def __init__(self,n_feature):
		super(Lnet,self).__init__()
		self.linear=nn.Linear(n_feature,1)
	def forward(self,x):
		y=self.linear(x)
		return y
net=Lnet(num_inputs)
print(net)#可以打印出网络的结构

事实上我们还可以用nn.Sequential来更加方便地搭建网络，Sequential是一个有序的容器，网络层将按照在传入Sequential的顺序依次被添加到计算图中。

# 写法一
net = nn.Sequential(
    nn.Linear(num_inputs, 1)
    # 此处还可以传入其他层
    )

# 写法二
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......

# 写法三
from collections import OrderedDict
net = nn.Sequential(OrderedDict([
          ('linear', nn.Linear(num_inputs, 1))
          # ......
        ]))

print(net)
print(net[0])

net.parameters()

可以查看模型所有的可学习参数,返回一个生成器

for param in net.parameters():
    print(param)

Parameter containing:
tensor([[-0.0277, 0.2771]], requires_grad=True)
Parameter containing:
tensor([0.3395], requires_grad=True)

.unsqueeze(0)

注意：torch.nn仅支持输入一个batch的样本不支持单个样本输入，如果只有单个样本，可使用input.unsqueeze(0)来添加一维。

初始化模型参数

在使用net前，我们需要初始化模型参数，如线性回归模型中的权重和偏差。PyTorch在init模块中提供了多种参数初始化方法。这里的init是initializer的缩写形式。我们通过init.normal_将权重参数每个元素初始化为随机采样于均值为0、标准差为0.01的正态分布。偏差会初始化为零。

from torch.nn import init

init.normal_(net[0].weight, mean=0, std=0.01)
init.constant_(net[0].bias, val=0)  # 也可以直接修改bias的data: net[0].bias.data.fill_(0)

net[0]这样根据下标访问子模块的写法只有当net是个ModuleList或者Sequential实例时才可以。

优化算法

import torch.optim as optim

optimizer = optim.SGD(net.parameters(), lr=0.03)
print(optimizer)

SGD (
Parameter Group 0
dampening: 0
lr: 0.03
momentum: 0
nesterov: False
weight_decay: 0
)
还可以为不同子网络设置不同的学习率，这在finetune时经常用到。

optimizer =optim.SGD([
                # 如果对某个参数不指定学习率，就使用最外层的默认学习率
                {'params': net.subnet1.parameters()}, # lr=0.03
                {'params': net.subnet2.parameters(), 'lr': 0.01}
            ], lr=0.03)

softmax回归

.argmax(dim=1)

返回y_hat每行中最大元素的索引，且返回的结果与变量y形状相同（这里y是label）