PTA---算法2021秋_动态规划
文章目录
-
- 0-1背包
- 求解矩阵最小路径和问题
- 7-2 回文串问题
- 7-3 石子合并
0-1背包
给定n(n<=100)种物品和一个背包。物品i的重量是wi,价值为vi,背包的容量为C(C<=1000)。问:应如何选择装入背包中的物品,使得装入背包中物品的总价值最大? 在选择装入背包的物品时,对每种物品i只有两个选择:装入或不装入。不能将物品i装入多次,也不能只装入部分物品i。
输入格式:
共有n+1行输入: 第一行为n值和c值,表示n件物品和背包容量c; 接下来的n行,每行有两个数据,分别表示第i(1≤i≤n)件物品的重量和价值。
输出格式:
输出装入背包中物品的最大总价值。
输入样例:
在这里给出一组输入。例如:
5 10
2 6
2 3
6 5
5 4
4 6
结尾无空行
输出样例:
在这里给出相应的输出。例如:
15

import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int sumW = in.nextInt();
long []val = new long[n];
long []w = new long[n];
for(int i = 0;i < n;i++){
w[i] = in.nextLong();
val[i] = in.nextLong();
}
long [][]dp = new long[n + 1][sumW + 1]; //dp[x][y]表示第x件物品,背包容量为y时的情况
for(int i = 1;i < n + 1;i++){
for(int j = 1;j < sumW + 1;j++){
if(j >= w[i - 1]){
//当背包容量大于物品重量
dp[i][j] = Math.max(dp[i - 1][j - (int)w[i - 1]] + val[i - 1],dp[i - 1][j]);
}else {
dp[i][j] = dp[i - 1][j];
}
}
}
System.out.println(dp[n][sumW]);
}
}
求解矩阵最小路径和问题
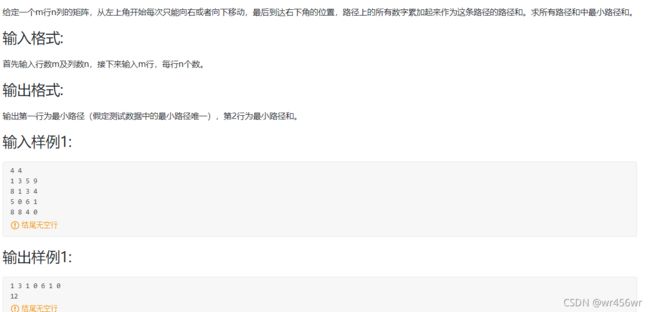
给定一个m行n列的矩阵,从左上角开始每次只能向右或者向下移动,最后到达右下角的位置,路径上的所有数字累加起来作为这条路径的路径和。求所有路径和中最小路径和。
输入格式:
首先输入行数m及列数n,接下来输入m行,每行n个数。
输出格式:
输出第一行为最小路径(假定测试数据中的最小路径唯一),第2行为最小路径和。
输入样例1:
4 4
1 3 5 9
8 1 3 4
5 0 6 1
8 8 4 0
结尾无空行
输出样例1:
1 3 1 0 6 1 0
12
做题思路:
对于每步有两个选择,向左走或者向右走,设OPT(i)表示到达第i步最少路径,则OPT(7)就为题目的左上角到达右下角的最少路径(最少走7步),V(i)表示第i步的开销。
对于OPT(i)= {OPT(i - 1)(向下),OPT(i - 1)(向右)}mim + V(i)
对于直接计算出最少路径较为简单,但是题目还需要输出最少经过的路径,之后将一个Path数组模拟OPT的选择情况,从后向前统计Path的路径标记即可。
对于java代码好像是过不了第二个测试用例,超时,这里给出了java和c的两种代码:
package PTA.DynamicProgramming;
import java.util.Arrays;
import java.util.Scanner;
public class Program4 {
/**
* 给定一个m行n列的矩阵,从左上角开始每次只能向右或者向下移动,最后到达右下角的位置,路径上的所有数字累加起来作为这条路径的路径和。求所有路径和中最小路径和
*/
//递归解决
// public static void main(String[] args) {
// Scanner in = new Scanner(System.in);
// int row = in.nextInt();
// int col = in.nextInt();
// int [][]matrix = new int[row][col];
// for(int i = 0;i < row;i++){
// for (int j = 0;j < col;j++){
// matrix[i][j] = in.nextInt();
// }
// }
// System.out.println(OPT(matrix,row - 1,col - 1));
// }
// static int OPT(int [][]matrix,int x,int y){
// if(x == 0 && y == 0){
// return 1;
// }
// if((x >= 0 && x < matrix.length) && (y >= 0 && y < matrix[0].length))
// return Math.min(OPT(matrix,x - 1,y),OPT(matrix,x,y - 1)) + matrix[x][y];
// else {
// return Integer.MAX_VALUE;
// }
// }
//dp解决
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int row = in.nextInt();
int col = in.nextInt();
int [][]matrix = new int[row][col];
// 数据输入
for(int i = 0;i < row;i++){
for (int j = 0;j < col;j++){
matrix[i][j] = in.nextInt();
}
}
//数据生成
// matrix = setMatrix(row,col,20);
//dp数组建立
int [][]dp = new int[row][col];
boolean [][]path = new boolean[row][col];
path[0][0] = true;
for(int i = 0;i < row ;i++){
for(int j = 0;j < col ;j++){
if(i == 0 && j == 0)
dp[i][j] = matrix[i][j];
else if(i == 0){
dp[i][j] = dp[i][j - 1] + matrix[i][j];
}else if(j == 0){
dp[i][j] = dp[i - 1][j] + matrix[i][j];
}else {
int min;
if(dp[i - 1][j] > dp[i][j - 1]){
min = dp[i][j - 1];
path[i][j - 1] = true;
}else if(dp[i - 1][j] < dp[i][j - 1]){
min = dp[i - 1][j];
path[i - 1][j] = true;
}else {
min = dp[i - 1][j];
path[i - 1][j] = true;
path[i][j - 1] = true;
}
dp[i][j] = min + matrix[i][j];
}
}
}
int []pathOne = new int[row + col - 1];
int step = row + col - 2;
int x = row - 1,y = col - 1;
for(int i = 0;i <= row + col - 2;i++){
pathOne[step] = matrix[x][y];
if(y - 1 >= 0 && x - 1 >= 0 && path[x - 1][y] && path[x][y - 1]){
if(dp[x - 1][y] > dp[x][y - 1]){
y--;
}else {
x--;
}
}
else if(y - 1 >= 0 && path[x][y - 1]){
y--;
}else if(x - 1 >= 0 && path[x - 1][y]){
x--;
}
step--;
}
for(int i = 0;i <= row + col - 2;i++){
System.out.print(pathOne[i] + " ");
}
System.out.println();
System.out.println(dp[row - 1][col - 1]);
}
//数据生成
// static int [][]setMatrix(int row,int col,int upper){
// int [][]matrix = new int[row][col];
// for(int i = 0;i < row;i++){
// for(int j = 0;j < col;j++){
// matrix[i][j] = (int )(Math.random() * upper);
// }
// }
// return matrix;
// }
}
/*
4 4
1 3 5 9
8 1 3 4
5 0 6 1
8 8 4 0
*/
c语言代码:
#include7-2 回文串问题
7-2 回文串问题 (20 分)
一个字符串,如果从左到右读和从右到左读是完全一样的,比如"aba",我们称其为回文串。现在给你一个字符串,可在任意位置添加字符,求最少添加几个字符,才能使其变成一个回文串。
输入格式:
任意给定的一个字符串,其长度不超过1000.
输出格式:
能变成回文串所需添加的最少字符数。
输入样例:
在这里给出一组输入。例如:
Ab3bd
结尾无空行
Abb
结尾无空行
输出样例:
在这里给出相应的输出。例如:
2

#include
#include
#include
#include
using namespace std;
int dp[1001][1001];
int main()
{
char ch1[1001];
char ch2[1001];
string s;
while(cin>>s)
{
for(int i=0;idp[i][j-1])dp[i][j]=dp[i-1][j];
else dp[i][j]=dp[i][j-1];
}
}
cout<<(len - dp[len][len])< 7-3 石子合并
7-3 石子合并 (30 分)
在一个圆形操场的四周摆放 N 堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的 2 堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。
试设计出一个算法,计算出将 N 堆石子合并成 1 堆的最小得分和最大得分。
输入格式:
数据的第 1 行是正整数 N ,表示有 N 堆石子。
第 2 行有 N 个整数,第 i 个整数 a
i
表示第 i 堆石子的个数。
输出格式:
输出共 2 行,第 1 行为最小得分,第 2 行为最大得分。
输入样例:
4
4 5 9 4
结尾无空行
输出样例:
43
54
#include